ਸਮੇਂ ਦਾ ਸੰਖੇਪ ਇਤਿਹਾਸ

ਮੂਲ ਲੇਖਕ : ਸਟੀਫਨ ਡਬਲਿਊ ਹਾਕਿੰਗ

ਅਨੁਵਾਦਕ : ਗੁਰਦਿੱਤ ਸਿੰਘ ਕੰਗ

ਮੁੱਖ ਸ਼ਬਦ

ਕੁਝ ਸਮਾਂ ਪਹਿਲਾਂ ਸੰਸਾਰ ਦੇ ਪ੍ਰਸਿੱਧ ਵਿਗਿਆਨੀ ਬਰਟਰੈਂਡੇ ਰਸਲ ਨੇ ਲੋਕਾਂ ਦੇ ਭਾਰੇ ਇਕੱਠ ਨੂੰ ਭਾਸ਼ਣ ਦੇਣ ਵੇਲੇ ਦੱਸਿਆ ਸੀ ਕਿ ਸਾਡੀ ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮਦੀ ਹੈਂ। ਕਮਰੇ ਦੇ ਪਿਛਲੇ ਪਾਸੇ ਬੈਠੀ ਇਕ ਵਿਰਧ ਮਧਰੀ ਜਿਹੀ ਜ਼ਨਾਨੀ ਨੇ ਉਠ ਕੇ ਕਿਹਾ; ਜੋ ਕੁਝ ਧਰਤੀ ਬਾਰੇ ਦੱਸਿਆ ਗਿਆ ਹੈ, ਉਹ ਨਿਰਾ ਕੂੜਾ ਹੈ। ਧਰਤੀ ਤਾਂ ਇਕ ਬਹੁਤ ਵੱਡੇ ਕਦਵਾਰ ਕੱਛੂ ਦੇ ਸਿਰ ਉੱਤੇ ਟਿਕੀ ਹੋਈ ਹੈ।

ਬਰਟਰੈਂਡੇ ਰਸਲ ਸੁਣ ਕੇ ਪਹਿਲਾਂ ਤਾਂ ਮੁਸਕਰਾਇਆ ਅਤੇ ਫੇਰ ਬੋਲਿਆ, “ਫੇਰ ਭਲਾ ਕੱਛੂ ਕਿਸ ਚੀਜ਼ ਉੱਤੇ ਟਿਕਿਆ ਹੋਇਆ ਹੈ? ਵਿਰਧ ਜ਼ਨਾਨੀ ਨੇ ਸੁਣ ਕੇ ਕਿਹਾ, “ਨੌਜਵਾਨ ਤੂੰ ਤਾਂ ਬਹੁਤ ਚਲਾਕ ਅਤੇ ਚਤਰ ਪੁਰਸ਼ ਹੈਂ। ਧਰਤੀ ਤਾਂ ਸੱਚਮੁੱਚ ਕੱਛੂ ਦੇ ਸਿਰ ਉੱਤੇ ਟਿਕੀ ਹੋਈ ਹੈ।”

ਧਰਤੀ ਬਾਰੇ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਕਈ ਭੁਲੇਖੇ ਹਾਲੇ ਵੀ ਮੌਜੂਦ ਹਨ। ਲੋਕ ਇਹ ਜਾਣਨਾ ਅਤੇ ਪੁੱਛਣਾ ਲੋਚਦੇ ਹਨ ਕਿ ਧਰਤੀ ਕਿੱਥੋਂ ਆਈ ਹੈ, ਇਸ ਦਾ ਸੁਭਾਓ ਕਿਸ ‘ਪ੍ਰਕਾਰ ਦਾ ਹੈ। ਇਸ ਵਿੱਚ ਸਾਡਾ ਸਥਾਨ ਕੀ ਹੈ ਅਤੇ ਇਹ ਕਿੱਥੇ ਜਾ ਰਹੀ ਹੈ ਅਤੇ ਅਸੀਂ ਕਿੱਥੋਂ ਆਏ ਹਾਂ?

ਅਜਿਹੇ ਅੰਧ-ਵਿਸ਼ਵਾਸ ਤੋਂ ਉਪਜੇ ਭੁਲੇਖਿਆਂ ਨੂੰ ਦੂਰ ਕਰਨ ਲਈ ਬਹੁਤ ਸਾਰੇ ਵਿਗਿਆਨੀਆਂ ਨੇ ਖੋਜ ਕੀਤੀ ਹੈ ਅਤੇ ਬਹੁਤ ਸਾਰੇ ਭੁਲੇਖੇ ਦੂਰ ਹੋ ਵੀ ਗਏ ਹਨ। ਇਸੇ ਸੰਧਰਵ ਵਿੱਚ ਵਰਤਮਾਨ ਸਮੇਂ ਦੇ ਉੱਘੇ ਵਿਦਵਾਨ ਵਿਗਿਆਨੀ ਮਿਸਟਰ ਸਟੀਫਨ ਹਾਕਿੰਗ, ਜੋ ਇੰਗਲੈਂਡ ਵਿਖੇ ਕੈਂਬਰਿਜ ਯੂਨੀਵਰਸਿਟੀ ਵਿੱਚ ਪ੍ਰੋਫ਼ੈਸਰ ਹਨ ਨੇ ਸਾਲਾਂ ਵਧੀ ਖੋਜ ਦੇ ਆਧਾਰ ‘ਤੇ “ਸਮੇਂ ਦਾ ਸੰਖੇਪ ਇਤਿਹਾਸ” (A Brief History of Time) ਪੁਸਤਕ ਲਿਖੀ ਹੈ। ਲੇਖਕ ਨੇ ਇਸ ਬਹੁ-ਮੁੱਲੀ ਅਤੇ ਗਿਆਨ-ਭਰਪੂਰ ਪੁਸਤਕ ਦਾ ਅਨੁਵਾਦ ਪੰਜਾਬੀ ਜਗਤ ਦੀ ਸੇਵਾ ਵਿੱਚ ਪੇਸ਼ ਕਰਨ ਦਾ ਉਪਰਾਲਾ ਕੀਤਾ ਹੈ। ਲੋਕ ਜਾਣਦੇ ਹਨ ਕਿ ਮਿਸਟਰ ਸਟੀਫਨ ਹਾਕਿੰਗ ਕਈ ਸਾਲਾਂ ਤੋਂ ਸਰੀਰਕ ਪੱਖੋਂ ਨਿਕਾਰਾ ਹੋ. ਚੁੱਕੇ ਹਨ, ਪ੍ਰੰਤੂ ਫੇਰ ਵੀ ਕੰਪਿਊਟਰ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਖੋਜ ਵਿੱਚ ਰੁੱਝੇ ਹੀ ਰਹਿੰਦੇ ਹਨ।

ਹੱਥਲੀ ਪੁਸਤਕ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਹਾਲੇ ਵੀ ਲੋਕ ਕਹਿੰਦੇ ਹਨ ਕਿ ਧਰਤੀ ਦਾ ਨਿਰਮਾਣ ਈਸ਼ਵਰ ਨੇ ਕੀਤਾ ਹੈ ਅਤੇ ਇਹ ਉਸ ਦੇ ਹੁਕਮ ਅਨੁਸਾਰ ਹੀ ਕਾਰਜਸ਼ੀਲ ਹੈ। ਇਹ ਨਿਰਾ ਅੰਧ-ਵਿਸ਼ਵਾਸ ਜਾਪਦਾ ਹੈ। ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਕੁਦਰਤੀ ਸ਼ਕਤੀਆਂ, ਅਰਥਾਤ ਹਵਾ, ਪਾਣੀ, ਅੱਗ ਅਤੇ ਮਿੱਟੀ ਦੇ ਕੰਮਾਂ ਉੱਤੇ ਕਿਸੇ ਬਾਹਰਲੀ ਸ਼ਕਤੀ ਦਾ ਕੰਟਰੋਲ ਨਹੀਂ ਹੈ। ਜਦੋਂ ਝੱਖੜ ਆਉਂਦਾ ਹੈ, ਬਾਰਸ਼ ਪੈਣ ਸਦਕਾ ਹੜ੍ਹ ਆਉਂਦੇ ਹਨ, ਗੜੇ ਪੈਂਦੇ ਹਨ, ਜਾਂ ਜੰਗਲਾਂ ਵਿੱਚ ਅੱਗ ਲੱਗ ਜਾਂਦੀ ਹੈ, ਜਾਂ ਬਿਜਲੀ ਲਿਸ਼ਕਦੀ ਹੈ, ਦੁਨੀਆਂ ਦਾ ਜਾਨੀ ਅਤੇ ਮਾਲੀ ਨੁਕਸਾਨ ਸ਼ਬਦਾਂ ਵਿੱਚ ਪ੍ਰਗਟ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ। ਜੇ ਇਹ ਸਭ ਕੁਝ ਈਸ਼ਵਰ ਦੇ ਹੁਕਮ ਨਾਲ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਉਹ ਦੁਨੀਆਂ ਦਾ ਹਿਤੈਸ਼ੀ ਨਹੀਂ ਹੈ। ਅਸਲ ਗੱਲ ਤਾਂ ਇਹ ਹੈ ਕਿ ਇਹ ਸਭ ਕੁਝ ਕੁਦਰਤੀ ਸ਼ਕਤੀਆਂ ਦੇ ਆਪਸੀ ਟਕਰਾਓ ਦਾ ਨਤੀਜਾ ਹੈ। ਨਹੀਂ ਤਾਂ ਈਸ਼ਵਰ ਨੂੰ ਲੋਕਾਂ ਦੇ ਜਾਨ ਮਾਲ ਦੀ ਰੱਖਿਆ ਹਿੱਤ ਇਨ੍ਹਾਂ ਸ਼ਕਤੀਆਂ ਨੂੰ ਰੋਕ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ। ਈਸ਼ਵਰ ਬਾਰੇ ਪ੍ਰੋ. ਮੋਹਨ ਸਿੰਘ ਨੇ ਆਪਣੀ ਕਵਿਤਾ ਦੇ ਆਰੰਭ ਵਿੱਚ ਲਿਖਿਆ ਸੀ।

“ਰੱਬ ਇਕ ਗੁੰਝਲਦਾਰ ਬੁਝਾਰਤ,

ਰੱਬ ਇਕ ਗੋਰਖ ਧੰਦਾ,

ਖੋਹਲਣ ਲੱਗਿਆਂ ਪੇਚ ਏਸ ਦੇ, ਕਾਫ਼ਰ ਹੋ ਜਾਵੇ ਬੰਦਾ,

ਕਾਫ਼ਰ ਹੋਣੋਂ ਡਰ ਕੇ ਜੀਵੇ, ਖੋਜੋਂ ਮੂਲ ਨਾ ਖੁੰਝੀਂ,

ਲਾਈ ਲਗ ਮੋਮਨ ਦੇ ਕੋਲੋਂ, ਖੋਜੀ ਕਾਫ਼ਰ ਚੰਗਾ।

ਸੋ ਉਮੀਦ ਹੈ ਕਿ ਹੱਥਲੀ ਪੁਸਤਕ ਪੜ੍ਹ ਕੇ ਲੋਕਾਂ ਨੂੰ ਧਰਤੀ ਬਾਰੇ ਕਾਫ਼ੀ ਸੰਤੋਸ਼ਜਨਕ ਚਾਨਣ ਹੋ ਜਾਵੇਗਾ ਅਤੇ ਅੰਧ-ਵਿਸ਼ਵਾਸ ਤੋਂ ਮੁਕਤੀ ਪ੍ਰਾਪਤ ਹੋ ਜਾਵੇਗੀ।

ਆਸ਼ਾਵਾਦੀ ਲੋਕ ਤਾਂ ਜਾਣਦੇ ਹਨ ਕਿ ਹਾਲੇ ਵੀ ਖੋਜ ਜਾਰੀ ਹੈ। ਐਉਂ ਜਾਪਦਾ ਹੈ ਕਿ ਧਰਤੀ ਪਹਿਲਾਂ ਤੋਂ ਹੀ ਮੌਜੂਦ ਸੀ। ਇਹ ਹੁਣ ਵੀ ਮੌਜੂਦ ਹੈ ਅਤੇ ਮੌਜੂਦ ਹੀ ਰਹੇਗੀ। ਸ਼ਾਇਦ ਇਸ ਦਾ ਕਾਲੇ ਖੂਹ ਦਾ ਰੂਪ ਧਾਰ ਕੇ ਅੰਤ ਨਾ ਹੋਵੇ ਅਤੇ ਸਾਰੇ ਇਸ ਦੇ ਸੁੰਦਰ ਵਾਤਾਵਰਣ ਦਾ ਅਨੰਦ ਮਾਣਦੇ ਰਹੀਏ। ਚਿੰਤਾ ਵਾਲੀ ਕੋਈ ਗੱਲ ਨਹੀਂ ਹੈ। ਸੁਨਹਿਰੇ ਭਵਿੱਖ ਦੀ ਉਮੀਦ ਵਿੱਚ ਪਾਠਕਾਂ ਦਾ ਹਿਤੂ।

-ਗੁਰਦਿੱਤ ਸਿੰਘ ਕੰਗ

ਸਾਡੀ ਧਰਤੀ ਦਾ ਚਿੱਤਰ

ਇਕ ਉੱਘੇ ਵਿਗਿਆਨੀ ਨੇ (ਕੁਝ ਸੱਜਣ ਕਹਿੰਦੇ ਹਨ ਕਿ ਉਹ ਵਿਗਿਆਨੀ ਬਰਟਰੈਂਡ ਰਸਲ ਸੀ) ਨੇ ਇਕ ਵੱਡੇ ਇਕੱਠ ਨੂੰ ਤਾਰਕ ਮੰਡਲ ਬਾਰੇ ਭਾਸ਼ਣ ਦਿੱਤਾ ਸੀ। ਉਸ ਨੇ ਦੱਸਿਆ ਸੀ ਕਿ ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਕਿਵੇਂ ਘੁੰਮਦੀ ਹੈ, ਅਤੇ ਸੂਰਜ ਤਾਰਿਆਂ ਦੇ ਵਿਸ਼ਾਲ ਝੁਰਮਟ ਦੇ ਕੇਂਦਰ ਦੁਆਲੇ ਕਿਵੇਂ ਚੱਕਰ ਲਾਉਂਦਾ ਹੈ, ਜਿਸ ਝੁਰਮਟ ਨੂੰ ਬ੍ਰਹਿਮੰਡ ਕਹਿੰਦੇ ਹਨ। ਭਾਸ਼ਣ ਦੇ ਅੰਤ ਸਮੇਂ ਇਕ ਮੱਧਰੀ ਜਿਹੀ ਬਿਰਧ ਇਸਤ੍ਰੀ ਨੇ, ਕਮਰੇ ਦੇ ਪਿਛਲੇ ਪਾਸੇ ਖਲੋ ਕੇ ਕਿਹਾ, “ਜੋ ਕੁਝ ਵੀ ਤੁਸੀਂ ਕਿਹਾ ਹੈ, ਉਹ ਰੱਦੀ ਕੂੜਾ ਹੈ। ਧਰਤੀ ਤਾਂ ਅਸਲ ਵਿੱਚ ਚਪਟੀ ਪਲੇਟ ਵਰਗੀ ਹੈ ਅਤੇ ਇਕ ਬਹੁਤ ਵੱਡੇ ਆਕਾਰ ਵਾਲੇ ਕੱਛੂ ਦੇ ਆਸਰੇ ਟਿਕੀ ਹੋਈ ਹੈ।” ਵਿਗਿਆਨੀ ਖਿੜ ਖਿੜਾ ਕੇ ਮੁਸਕਰਾਇਆ ਅਤੇ ਫੇਰ ਉੱਤਰ ਵਿੱਚ ਕਿਹਾ, “ਕੱਛੂ ਕਿਹੜੀ ਸ਼ੈਅ ਉੱਤੇ ਟਿਕਿਆ ਹੋਇਆ ਹੈ ?” ਉਹ · ਇਸਤ੍ਰੀ ਉੱਤਰ ਸੁਣ ਕੇ ਬੋਲੀ, ਨੌਜਵਾਨ ਤੂੰ ਬਹੁਤ ਚਲਾਕ ਅਤੇ ਚਤੁਰ ਪੁਰਸ਼ ਹੈਂ। ਪਰ ਧਰਤੀ ਤਾਂ ਕਛੂਆਂ ਦੇ ਆਸਰੇ ਖੜ੍ਹੀ ਹੈ!”

ਲੋਕਾਂ ਦੀ ਬਹੁਤ ਵੱਡੀ ਸੰਖਿਆ ਜੇ ਇਸ ਧਰਤੀ ਨੂੰ ਕਛੂਆਂ ਦਾ ਇਕ ਬਹੁਤ ਵੱਡਾ ਮੀਨਾਰ ਸਮਝਦੀ ਹੋਵੇ, ਤਾਂ ਇਕ ਮਜ਼ਾਕ ਜਾਂ ਮਖ਼ੌਲ ਵਾਲੀ ਗੱਲ ਹੈ, ਪਰੰਤੂ ਅਸੀਂ ਇਹ ਕਿਉਂ ਸਮਝਦੇ ਹਾਂ ਕਿ ਸਾਨੂੰ ਵਧੇਰੇ ਗਿਆਨ ਹੈ ? ਅਸੀਂ ਧਰਤੀ ਬਾਰੇ ਕੀ ਜਾਣਦੇ ਹਾਂ ਅਤੇ ਅਜਿਹਾ ਕਿਉਂ ਅਤੇ ਕਿਵੇਂ ਸਮਝਦੇ ਹਾਂ ? ਧਰਤੀ ਕਿੱਥੋਂ ਆਈ ਹੈ ਅਤੇ ਕਿਹੜੇ ਪਾਸੇ ਜਾ ਰਹੀ ਹੈ ? ਕੀ ਇਸ ਧਰਤੀ ਦਾ ਕੋਈ ਅਰੰਭ ਹੈ, ਜੇ ਅਜਿਹਾ ਅਰੰਭ ਹੈ, ਤਾਂ ਉਸ ਤੋਂ ਪਹਿਲਾਂ ਕੀ ਕੁਝ ਵਾਪਰ ਚੁੱਕਾ ਸੀ ? ਸਮੇਂ ਦਾ ਸੁਭਾਅ ਕਿਸ ਪ੍ਰਕਾਰ ਦਾ ਹੈ ? ਕੀ ਕਦੇ ਇਸ ਦਾ ਅੰਤ ਵੀ ਹੋ ਜਾਵੇਗਾ ? ਹੁਣੇ ਜਿਹੇ ਫਿਜਿਕਸ ਵਿੱਚ ਹੋਏ ਵਿਕਾਸ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਇਨ੍ਹਾਂ ਚਰੋਕਣੇ ਲਟਕ ਰਹੇ ਪ੍ਰਸ਼ਨਾਂ ਦਾ ਕੀ ਉੱਤਰ ਹੈ, ਜਿਹੜਾ ਵਿਕਾਸ ਅਦਭੁੱਤ ਤਕਨੀਕੀ ਪ੍ਰਾਪਤੀਆਂ ਨੇ ਕਿਸੇ ਹੱਦ ਤੱਕ ਸੰਭਵ ਬਣਾ ਦਿੱਤਾ ਹੈ। ਕਿਸੇ ਦਿਨ ਇਹ ਉੱਤਰ ਸਾਨੂੰ ਇੰਨੇ ਸੌਖੇ ਅਤੇ ਪ੍ਰਤੱਖ ਲੱਗ ਸਕਦੇ ਹਨ, ਜਿਵੇਂ ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮ ਰਹੀ ਹੈ, ਜਾਂ ਕਛੂਆਂ ਦੇ ਮੀਨਾਰ ਵਾਂਗ ਇਕ ਮਖੌਲ। ਨਿਰਣਾ ਤਾਂ ਸਮਾਂ ਹੀ ਕਰੇਗਾ, ਭਾਵੇਂ ਕਦੇ ਵੀ ਆਉਣ ਵਾਲਾ ਸਮਾਂ।

340 ਸਾਲ ਪੂਰਵ, ਯੂਨਾਨ ਦੇ ਫਿਲਾਸਫਰ ਅਰਸਤੂ ਆਪਣੀ ਪੁਸਤਕ “On the Steavens” “ਆਕਾਸ਼ ਉੱਤੇ” ਵਿੱਚ ਦੋ ਨਿੱਗਰ ਦਲੀਲਾਂ ਦੇਣ ਯੋਗ ਹੋ ਗਿਆ ਸੀ, ਜਿਨ੍ਹਾਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਇਹ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾ ਸਕਦਾ ਸੀ ਕਿ ਧਰਤੀ ਸੱਚਮੁੱਚ ਗੋਲ ਹੈ, ਇਹ ਪਧਰੀ ਪਲੇਟ ਵਰਗੀ ਨਹੀਂ ਹੈ। ਪਹਿਲੀ ਦਲੀਲ ਇਹ ਕਿ ਚੰਦ ਗ੍ਰਹਿਣ ਉਦੋਂ ਲੱਗਦੇ ਹਨ, ਜਦੋਂ ਧਰਤੀ ਸੂਰਜ ਅਤੇ ਚੰਦ ਦੇ ਐਨ ਵਿਚਕਾਰ ਆ ਜਾਂਦੀ ਹੈ। ਧਰਤੀ ਦਾ ਚੰਦ ਉੱਤੇ ਜੋ ਪਰਛਾਵਾਂ ਪੈਂਦਾ ਹੈ, ਉਹ ਗੋਲ ਹੁੰਦਾ ਹੈ, ਅਜਿਹਾ ਇਸੇ ਕਰਕੇ ਸੰਭਵ ਹੋ ਸਕਦਾ ਹੈ, ਜੇ ਧਰਤੀ ਗੋਲ ਹੋਵੇ, ਜੇ ਧਰਤੀ ਇਕ ਚਪਟੀ ਪਲੇਟ ਵਰਗੀ ਹੁੰਦੀ ਤਾਂ ਇਹ ਪਰਛਾਵਾਂ ਟੇਢਾ ਹੋਣਾ ਸੀ, ਜੇ ਗ੍ਰਹਿਣ ਐਨ ਉਸ ਵੇਲੇ ਨਾ ਲੱਗਿਆ ਕਰੇ ਜਦੋਂ ਸੂਰਜ ਉਸ ਪਲੇਟ ਦੇ ਕੇਂਦਰ ਬਿੰਦੂ ਉੱਤੇ ਸਿੱਧਾ ਨਾ ਆਇਆ ਕਰਦਾ। ਦੂਜੀ ਦਲੀਲ ਇਹ ਸੀ ਕਿ ਯੂਨਾਨੀ ਜਾਣਦੇ ਸਨ ਕਿ ਧਰੂ ਤਾਰਾ ਦੱਖਣ ਵਿੱਚੋਂ ਦੇਖਿਆਂ ਨੀਵਾਂ ਲੱਗਦਾ ਸੀ ਅਤੇ ਉੱਤਰੀ ਖੰਡ ਵਿੱਚ ਇਹ ਤਾਰਾ ਉਚੇਰਾ ਲੱਗਦਾ ਸੀ। ਕਿਉਂਕਿ ਉਹ ਆਪਣੀਆਂ ਯਾਤਰਾਵਾਂ ਦੌਰਾਨ ਦੇਖ ਚੁੱਕੇ ਸਨ, ਕਿ ਧਰੂ ਤਾਰਾ ਉੱਤਰੀ ਸਿਰੇ ਉੱਤੇ ਹੈ। ਜਿੱਥੇ ਦੇਖਿਆਂ, ਇਹ ਦੇਖਣ ਵਾਲੇ ਦੇ ਐਨ ਸਿਰ ਉੱਤੇ ਨਜ਼ਰ ਆਉਂਦਾ ਸੀ, ਪਰ ਮੱਧ-ਰੇਖਾ ‘ਤੇ ਜਾ ਕੇ ਦੇਖਣ ਵਾਲੇ ਨੂੰ ਇਹ ਦਿਸ-ਹਦੇ ਦੇ ਨੇੜੇ ਥੱਲੇ ਨਜ਼ਰ ਆਉਂਦਾ ਸੀ। ਮਿਸਰ ਅਤੇ ਯੂਨਾਨ ਵਿੱਚੋਂ ਧਰੂ ਤਾਰੇ ਦੀ ਸਥਿਤੀ ਦੇ ਅੰਤਰ ਨੂੰ ਮੁੱਖ ਰੱਖ ਕੇ, ਅਰਸਤੂ ਨੇ ਇਹ ਅਨੁਮਾਨ ਵੀ ਲਾ ਦਿੱਤਾ ਸੀ ਕਿ ਧਰਤੀ ਦੀ ਗੋਲਾਈ ਚਾਰ ਲੱਖ ਸਟੇਡੀਆ ਹੈ। ਇਸ ਗੱਲ ਦਾ ਪਤਾ ਨਹੀਂ ਹੈ ਕਿ ਸਟੇਡੀਅਮ ਦੀ ਲੰਬਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ? ਇਹ ਤਕਰੀਬਨ 200 ਗਜ਼ ਲੰਬਾ ਹੁੰਦਾ ਹੋਵੇਗਾ, ਜਿਸ ਅਨੁਸਾਰ ਧਰਤੀ ਦੀ ਅੱਜ ਕੱਲ੍ਹ ਦੀ ਗੋਲਾਈ ਨਾਲੋਂ ਅਰਸਤੂ ਦਾ ਅਨੁਮਾਨ ਦੁੱਗਣਾ ਬਣਦਾ ਹੈ। ਯੂਨਾਨੀ ਤਾਂ ਇਕ ਤੀਜੀ ਦਲੀਲ ਇਹ ਵੀ ਦਿੰਦੇ ਸਨ ਕਿ ਧਰਤੀ ਗੋਲ ਹੋਣ ਦਾ ਸਬੂਤ ਇਸ ਗੱਲ ਤੋਂ ਵੀ ਮਿਲਦਾ ਹੈ ਕਿ ਦਿਸ-ਹੱਦੇ ਵੱਲੋਂ ਆਉਣ ਵਾਲੇ ਸਮੁੰਦਰੀ ਜਹਾਜ਼ ਦੇ ਬਾਦਵਾਨ ਪਹਿਲਾਂ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ ਅਤੇ ਜਹਾਜ਼ ਦਾ ਥੱਲਾ ਕਿਤੇ ਮਗਰੋਂ ਜਾ ਕੇ, ਜਹਾਜ਼ ਨੇੜੇ ਆਉਣ ਸਮੇਂ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ।

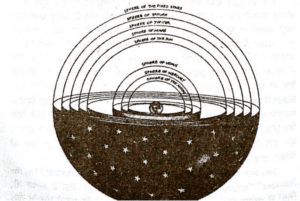
ਅਰਸਤੂ ਦੇ ਖ਼ਿਆਲ ਵਿੱਚ ਧਰਤੀ ਇੱਕੋ ਥਾਂ ‘ਤੇ ਖਲੋਤੀ ਸੀ ਅਤੇ ਸੂਰਜ, ਚੰਦ, ਗ੍ਰਹਿ ਅਤੇ ਤਾਰੇ ਧਰਤੀ ਦੁਆਲੇ ਘੁੰਮਦੇ ਸਨ। ਉਸ ਦਾ ਇਹ ਵਿਸ਼ਵਾਸ ਇਸ ਲਈ ਸੀ ਕਿ ਉਹ ਅਨੁਭਵ ਕਰਦਾ ਸੀ ਕਿ ਧਰਤੀ ਸਮੁੱਚੇ ਬ੍ਰਹਿਮੰਡ ਦਾ ਕੇਂਦਰ ਬਿੰਦੂ ਸੀ ਅਤੇ ਗੋਲ ਚੱਕਰ ਪੂਰਨ ਤੌਰ ‘ਤੇ ਨਿਰਵਿਘਨ ਸਨ। ਇਸ ਅਨੁਭਵ ਦਾ ਆਧਾਰ ਕੀ ਸੀ, ਕੁਝ ਪਤਾ ਨਹੀਂ ਹੈ। ਇਸ ਵਿਚਾਰ ਦੀ ਪਰੌੜਤਾ ਦੂਜੀ ਈਸਵੀ ਵਿੱਚ Ptolemy (ਟੌਮੀ) ਨੇ ਵੇਰਵੇ ਸਹਿਤ ਕਰ ਦਿੱਤੀ ਸੀ ਕਿ ਧਰਤੀ ਦੇ ਦੁਆਲੇ ਅੱਠ ਗ੍ਰਹਿ–ਸੂਰਜ, ਚੰਦਰ, ਤਾਰੇ ਅਤੇ ਹੋਰ ਪੰਜ ਗ੍ਰਹਿ ਜਿਨ੍ਹਾਂ ਦੇ ਉਸ ਵੇਲੇ ਨਾਮ ਸਨ-ਮਰਕਰੀ, ਵੀਨਸ, ਮਾਰੀਸ਼, ਜੁਪਿਟਰ ਅਤੇ ਸ਼ਨਿਚਰ ਸਨ, ਫੈਲੇ ਹੋਏ ਸਨ ਅਤੇ ਧਰਤੀ ਇਨ੍ਹਾਂ ਦੇ ਐਨ ਕੇਂਦਰ ਵਿੱਚ ਸਥਿਤ ਸੀ।

(ਤਸਵੀਰ 1.1.) ਇਹ ਗ੍ਰਹਿ ਆਪਣੇ-ਆਪਣੇ ਭੂਗੋਲਾਂ ਦੇ ਦੁਆਲੇ ਛੋਟੇ-ਛੋਟੇ ਚੱਕਰ ਲਾਉਂਦੇ ਸਨ, ਜਿਨ੍ਹਾਂ ਸਦਕਾ ਉਨ੍ਹਾਂ ਦੇ ਆਕਾਸ਼ ਵਿੱਚ ਬਣੇ ਹੋਏ ਪੇਚੀਦਾ ਮਾਰਗਾਂ ਦਾ ਪਤਾ ਲੱਗ ਸਕਦਾ ਸੀ। ਸਭ ਤੋਂ ਬਾਹਰਲੇ ਭੂਗੋਲ ਵਿੱਚ ਅਚੱਲ ਤਾਰੇ ਸਨ, ਜੋ ਇਕੋ ਥਾਂ ਟਿਕੇ ਹੋਏ ਸਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਆਪਸੀ ਰਸਤੇ ਕਾਇਮ ਰਹਿੰਦੇ ਸਨ ਅਤੇ ਉਹ ਸਾਰੇ ਦੇ ਸਾਰੇ ਸਮੂਹਕ ਤੌਰ ‘ਤੇ ਆਕਾਸ਼ ਵਿੱਚ ਘੁੰਮਦੇ ਰਹਿੰਦੇ ਸਨ। ਅੰਤਲੇ ਭੂਗੋਲ ਤੋਂ ਭਾਵ ਕੀ ਸੀ, ਕਦੇ ਵੀ ਸਪੱਸ਼ਟ ਨਹੀਂ ਸੀ ਕੀਤਾ ਗਿਆ। ਪਰੰਤੂ ਉਹ ਕੁਝ ਮਨੁੱਖ ਦੀ ਇਸ ਸਾਖਸ਼ਾਤ ਧਰਤੀ ਦਾ ਹਿੱਸਾ ਨਹੀਂ ਸੀ।

ਟੌਮੀ ਦੇ ਗੁਰ ਨਾਲ ਆਕਾਸ਼ ਦੀਆਂ ਧਰਤੀਆਂ ਦਾ ਕੁਝ ਸਹੀ ਅਨੁਮਾਨ ਲਾਇਆ ਜਾ ਸਕਦਾ ਸੀ ਕਿ ਉਹ ਕਿੱਥੇ-ਕਿੱਥੇ ਸਥਿਤ ਹਨ ? ਪਰੰਤੂ ਇਨ੍ਹਾਂ ਦੀ ਸਥਿਤੀ ਦਾ ਸਹੀ- ਸਹੀ ਪਤਾ ਲਾਉਣ ਲਈ ਉਹ ਫ਼ਰਜ਼ ਕਰ ਲੈਂਦਾ ਸੀ ਕਿ ਚੰਦ ਅਜਿਹੇ ਰਸਤੇ ਉੱਤੇ ਚਲਦਾ ਹੈ, ਜਿਸ ਅਨੁਸਾਰ ਕਦੇ-ਕਦੇ ਚੰਦ ਦਾ ਆਕਾਰ ਦੂਜੇ ਸਮਿਆਂ ਨਾਲੋਂ ਦੁਗਣਾ ਨਜ਼ਰ ਆਉਂਦਾ ਸੀ। ਟੌਮੀ ਇਸ ਗੁਰ ਦੀ ਊਣਤਾਈ ਨੂੰ ਸਮਝਦਾ ਸੀ, ਪਰ ਉਸ ਦੇ ਗੁਰ ਨੂੰ ਅੰਸ਼ਕ ਤੌਰ ‘ਤੇ ਪ੍ਰਵਾਨ ਕਰ ਲਿਆ ਗਿਆ ਸੀ, ਭਾਵੇਂ ਸੰਸਾਰਕ ਪੱਧਰ ‘ਤੇ ਇਹ ਗੁਰ ਪ੍ਰਵਾਨ ਨਹੀਂ ਸੀ ਚੜ੍ਹਿਆ। ਇਸ ਗੁਰ ਨੂੰ ਈਸਾਈ ਧਰਮ ਨੇ ਸਵੀਕਾਰ ਕਰ ਲਿਆ ਸੀ ਕਿਉਂਕਿ ਇਸ ਭੂਗੋਲ ਦਾ ਚਿੱਤਰ ਉਸ ਧਰਮ ਦੇ ਗ੍ਰੰਥ ਨਾਲ ਮੇਲ ਖਾਂਦਾ ਸੀ। ਕਿਉਂਕਿ ਅਜਿਹਾ ਕਰਨ ਦਾ ਇਹ ਲਾਭ ਸੀ ਕਿ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਅਚੱਲ ਤਾਰਿਆਂ ਦੇ ਬਾਹਰ-ਵਾਰ ਸਵਰਗ ਅਤੇ ਨਰਕ ਲਈ ਚੌਖੀ ਥਾਂ ਪ੍ਰਾਪਤ ਹੋ ਸਕਦੀ ਸੀ।

ਪਰੰਤੂ 1514 ਈਸਵੀ ਵਿੱਚ ਪੋਲੈਂਡ ਦੇ ਪੁਜਾਰੀ ਨਿਕੋਲਸ ਕੋਪਰਨਿਕਸ ਨੇ ਇਸ ਨਾਲੋਂ ਸੁਖਾਲਾ ਗੁਰ ਦੱਸ ਦਿੱਤਾ। (ਪਹਿਲਾ ਤਾਂ ਈਸਾਈ ਧਰਮ ਵੱਲੋਂ ਨਾਸਤਕ ਐਲਾਨੇ ਜਾਣ ਤੋਂ ਡਰਦਿਆਂ ਉਸ ਨੇ ਆਪਣਾ ਗੁਰ ਗੁੰਮਨਾਮ ਰਹਿ ਕੇ ਪ੍ਰਚਾਰਿਆ)। ਇਸ ਤਰ੍ਹਾਂ ਪੂਰੀ ਸਦੀ ਬੀਤਣ ਉਪਰੰਤ ਉਸ ਦੇ ਗੁਰ ਵੱਲ ਧਿਆਨ ਦਿੱਤਾ ਗਿਆ ਸੀ ਜਿਸ ਅਨੁਸਾਰ ਧਰਤੀ ਤਾਂ ਇਕ ਕੇਂਦਰ ਬਿੰਦੂ ਸੀ ਅਤੇ ਬਾਕੀ ਗ੍ਰਹਿ ਅਤੇ ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮ ਰਹੇ ਸਨ। ਇਸ ਦੇ ਉਪਰੰਤ ਦੋ ਤਾਰਾ ਵਿਗਿਆਨੀਆਂ, ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇਕ ਜਰਮਨੀ ਦਾ Johanson Kepler (ਜਾਨਸਨ ਕੈਪਲਰ) ਅਤੇ ਦੂਜਾ ਇਟਲੀ ਦਾ ਵਸਨੀਕ ਗਲੀਲੀਓ ਗਲੇਲੀ ਸੀ, ਨੇ ਖੁੱਲ੍ਹਮ-ਖੁਲ੍ਹੇ ਤੌਰ ‘ਤੇ ਕੋਪਰਨਿਕਸ ਦੇ ਗੁਰ ਦੀ ਪੁਸ਼ਟੀ ਕਰਨੀ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀ ਸੀ, ਭਾਵੇਂ ਇਸ ਗੁਰ ਵਿੱਚ ਦੱਸੇ ਗਏ ਘੁਮੇਰ ਅਸਲੀ ਚੱਕਰਾਂ ਨਾਲ ਦੇਖਣ ਵਿੱਚ ਮੇਲ ਨਹੀਂ ਸਨ ਖਾਂਦੇ। ਅਰਸਤੂ ਅਤੇ ਕੋਪਰਨਿਕਸ ਦੇ ਗੁਰਾਂ ਦਾ ਭੋਗ ਤਾਂ 1609 ਈਸਵੀ ਵਿੱਚ ਹੀ ਪੈ ਗਿਆ ਸੀ। ਉਸ ਸਾਲ ਗਲੀਲੀਓ ਨੇ ਆਕਾਸ਼ ਦੀ ਖੋਜ ਦੂਰਬੀਨ ਨਾਲ ਕਰਨੀ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀ ਸੀ, ਜਿਸ ਦੀ ਕਾਢ ਹੁਣੇ-ਹੁਣੇ ਹੋਈ ਸੀ। -ਜਦੋਂ ਉਸ ਨੇ ਜੁਪੀਟਰ ਤਾਰੇ ਨੂੰ ਵਾਚਿਆ ਤਾਂ ਉਸ ਨੂੰ ਪਤਾ ਲੱਗ ਗਿਆ ਕਿ ਇਸ ਦੇ ਨਾਲ ਹੋਰ ਕਿੰਨੇ ਹੀ ਉਪ-ਗ੍ਰਹਿ ਜਾਂ ਚੰਦ ਮੌਜੂਦ ਸਨ ਅਤੇ ਉਹ ਜੁਪੀਟਰ ਦੇ ਦੁਆਲੇ ਘੁੰਮ ਰਹੇ ਸਨ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਸੀ ਕਿ ਅਰਸਤੂ ਅਤੇ ਕੋਪਰਨਿਕਸ ਦੇ ਕਹਿਣ ਅਨੁਸਾਰ ਹਰ ਇਕ ਚੀਜ਼ (ਗ੍ਰਹਿ) ਨੂੰ ਸਿੱਧੇ ਤੌਰ ਤੇ ਧਰਤੀ ਦੁਆਲੇ ਘੁੰਮਣਾ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ। (ਤਾਂ ਵੀ ਅਜਿਹਾ ਵਿਸ਼ਵਾਸ ਰੱਖਣਾ ਸੰਭਵ ਸੀ ਕਿ ਧਰਤੀ ਬ੍ਰਹਿਮੰਡ ਦੇ ਐਨ ਵਿਚਕਾਰ ਅਚੱਲ ਟਿਕੀ ਹੋਈ ਹੈ ਅਤੇ ਜੁਪੀਟਰ ਦੇ ਚੰਦ ਧਰਤੀ ਦੁਆਲੇ ਅਗੜ-ਦੁਗੜੇ ਰਸਤਿਆਂ ਤੇ ਘੁੰਮ ਰਹੇ ਹਨ। ਪਰ ਜਾਪਦਾ ਐਉਂ ਸੀ ਕਿ ਉਹ ਜੁਪੀਟਰ ਦੇ ਦੁਆਲੇ ਹੀ ਘੁੰਮ ਰਹੇ ਹਨ। ਪਰ ਕੋਪਰਨਿਕਸ ਦਾ ਗੁਰ ਕਾਫ਼ੀ ਸੌਖਾ ਅਤੇ ਸਰਲ ਸੀ। ਉਸੇ ਵੇਲੇ ਜਾਨਸਨ ਕੈਪਲਰ ਨੇ ਕੋਪਰਨਿਕਸ ਦੇ ਗੁਰ ਵਿੱਚ ਸੋਧ ਕਰਕੇ ਸੁਝਾਅ ਦਿੱਤਾ ਸੀ ਕਿ ਗ੍ਰਹਿ ਗੋਲ ਚੱਕਰ ਨਹੀਂ ਲਾਉਂਦੇ, ਸਗੋਂ ਉਨ੍ਹਾਂ ਦੇ ਰਸਤਿਆਂ ਵਿੱਚ ਮੋੜ ਜਾਂ ਡਲ੍ਹਕ ਹੈ। ਹੁਣ ਭਵਿੱਖਬਾਣੀ ਕਰਨ ਅਤੇ ਦੇਖਣ ਵਿੱਚ ਸਮਾਨਤਾ ਪ੍ਰਤੀਤ ਹੋਣ ਲੱਗ ਪਈ ਸੀ।

ਜਿੱਥੋਂ ਤੱਕ ਕੈਪਲਰ ਦਾ ਸੰਬੰਧ ਸੀ, ਟੇਢੇ-ਮੇਢੇ ਰਸਤਿਆਂ ਵਾਲਾ ਵਿਚਾਰ ਇਕ ਫਰਜ਼ਕਾਰੀ ਹੀ ਸੀ, ਸਗੋਂ ਨਿਰੀ ਬੇਤੁਕੀ, ਕਿਉਂਕਿ ਅਜਿਹੇ ਰਸਤੇ ਗੋਲ ਚੱਕਰਾਂ ਦੇ ਰਸਤਿਆਂ ਨਾਲੋਂ ਤਸੱਲੀਬਖ਼ਸ਼ ਸਨ । ਜਦੋਂ ਉਸ ਨੂੰ ਅਚਾਨਕ ਹੀ ਇਹ ਮਹਿਸੂਸ ਹੋਇਆ ਕਿ ਟੇਢੇ-ਮੇਢੇ ਰਸਤੇ ਦੇਖਣ ਵਿੱਚ ਪੂਰਨ ਤੌਰ ‘ਤੇ ਮੇਲ ਖਾਂਦੇ ਸਨ, ਤਾਂ ਵੀ ਉਹ ਇਹ ਨਾ ਮੰਨਿਆ ਕਿ ਇਸ ਖ਼ਿਆਲ ਨਾਲ ਮਿਲਦੇ-ਜੁਲਦੇ ਹਨ ਕਿ ਗ੍ਰਹਿ ਚੁੰਬਕ ਸ਼ਕਤੀ ਸਦਕਾ ਹੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮਣ ਲਈ ਮਜਬੂਰ ਹਨ ਇਸੇ ਵਿਚਾਰ ਦੀ ਵਿਆਖਿਆ, ਬਹੁਤ ਪਛੜ ਕੇ, 1687 ਈਸਵੀ ਵਿੱਚ ਹੋ ਸਕੀ। ਜਦੋਂ ਸਰ ਇਜ਼ਾਕ ਨਿਊਟਨ ਨੇ ਆਪਣੀ भ्रमउव (Phizoosalphiae Naturals Principa Mathematica) यूवाप्तउ वीडी, ਜਿਹੜੀ ਸ਼ਾਇਦ ਫਿਜ਼ੀਕਲ ਸਾਇੰਸ ਵਿੱਚ ਛਪਣ ਵਾਲੀ ਸਭ ਤੋਂ ਵੱਧ ਮਹਤੱਤਾ ਵਾਲੀ ਰਚਨਾ ਸੀ। ਇਸ ਪੁਸਤਕ ਵਿੱਚ, ਨਿਊਟਨ ਨੇ ਨਾ ਕੇਵਲ ਇਹ ਗੁਰ ਹੀ ਪੇਸ਼ ਕੀਤਾ ਕਿ ਪੁਲਾੜ ਵਿੱਚ ਗ੍ਰਹਿ ਆਕਾਸ਼ ਅਤੇ ਸਮੇਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਕਿਵੇਂ ਘੁੰਮ ਰਹੇ ਹਨ, ਸਗੋਂ ਉਸ ਨੇ ਗ੍ਰਹਿ ਦੀ ਗਤੀ ਦਾ ਵਿਸ਼ਲੇਸ਼ਨ ਕਰਨ ਲਈ ਲੋੜੀਂਦੀ ਗਣਿਤ ਵਿਧੀ ਵੀ ਲੱਭ ਲਈ ਸੀ। ਇਸ ਤੋਂ ਇਲਾਵਾ, ਨਿਊਟਨ ਨੇ ਵਿਸ਼ਵ ਵਿਆਪੀ ਖਿੱਚ (Gravity) ਦਾ ਗੁਰ ਵੀ ਲੱਭ ਲਿਆ ਸੀ, ਜਿਸ ਅਨੁਸਾਰ ਇਸ ਸ਼ਕਤੀ ਦੁਆਰਾ ਪੁਲਾੜ ਦਾ ਹਰ ਇਕ ਗ੍ਰਹਿ ਦੂਜੇ ਗ੍ਰਹਿ ਵੱਲ ਖਿੱਚਿਆ ਜਾਂਦਾ ਹੈ। ਜਿਤਨੇ ਆਕਾਰ ਵਿੱਚ ਸ਼ਕਤੀਸ਼ਾਲੀ ਅਤੇ ਵੱਡੇ ਗ੍ਰਹਿ ਹੁੰਦੇ ਹਨ, ਉੱਨੇ ਉਹ ਇਕ ਦੂਜੇ ਦੇ ਵਧੇਰੇ ਨੇੜੇ ਹੁੰਦੇ ਹਨ। ਇਸ ਸ਼ਕਤੀ ਸਦਕਾ ਹੀ ਚੀਜ਼ਾਂ ਧਰਤੀ ਉੱਤੇ ਡਿੱਗ ਪੈਂਦੀਆਂ ਹਨ। ਇਹ ਕਹਾਣੀ ਕਿ ਨਿਊਟਨ ਦੇ ਸਿਰ ਵਿੱਚ ਸਿਉ ਵਜਣ ਨਾਲ ਹੀ ਉਸ ਨੂੰ ਫੁਰਨਾ ਫੁਰਿਆ ਸੀ, ਮਨ-ਘੜਤ ਕਹਾਣੀ ਹੈ। ਨਿਊਟਨ ਨੇ ਤਾਂ ਕੇਵਲ ਇਹ ਕਿਹਾ ਸੀ ਕਿ “ਇਸ ਖਿੱਚ ਦਾ ਖ਼ਿਆਲ ਉਸ ਵੇਲੇ ਪੈਦਾ ਹੋਇਆ ਸੀ, ਜਦੋਂ ਉਹ ਸੋਚਾਂ ਵਿੱਚ ਡੁੱਬਿਆ ਹੋਇਆ ਸੀ ਅਤੇ ਇਕ ਸਿਉ ਦਾ ਦਾਣਾ ਧਰਤੀ ਤੇ ਡਿੱਗ ਪਿਆ ਸੀ।” ਨਿਊਟਨ ਨੇ ਇਹ ਸਾਬਤ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਇਸ ਖਿੱਚ ਦੀ ਸ਼ਕਤੀ ਦੇ ਅਧੀਨ ਚੰਦ ਧਰਤੀ ਦੇ ਦੁਆਲੇ ਟੇਢੇ-ਮੇਢੇ ਰਸਤੇ ਚੱਕਰ ਲਾਉਂਦਾ ਹੈ ਅਤੇ ਦੂਜੇ ਗ੍ਰਹਿ ਅਤੇ ਧਰਤੀ ਸੂਰਜ ਦੇ ਦੁਆਲੇ ਇਸੇ ਸ਼ਕਤੀ ਅਧੀਨ ਘੁੰਮ ਰਹੇ ਹਨ।

ਕੌਪਰਨਿਕਸ ਦਾ ਗੁਰ ਟੌਮੀ ਦੇ ਆਕਾਸ਼ੀ ਭੂਗੋਲਾਂ ਦੇ ਗੁਰ ਵੱਲੋਂ ਸੁਰਖਰੂ ਹੋ ਗਿਆ ਅਤੇ ਇਸ ਖ਼ਿਆਲ ਤੋਂ ਵੀ ਕਿ ਧਰਤੀ ਦੀ ਇਕ ਕੁਦਰਤੀ ਸੀਮਾ ਹੈ ਜਾਂ ਹੱਦ ਹੈ, ਕਿਉਂਕਿ ਇਕੋ ਥਾਂ ਖਲੋਤੇ ਰਹਿਣ ਵਾਲੇ ਤਾਰੇ ਉਸ ਵੇਲੇ ਵੀ ਆਪਣੀ ਥਾਂ ਤੋਂ ਨਹੀਂ ਹਿਲਦੇ ਜਦੋਂ ਧਰਤੀ ਦੇ ਆਪਣੇ ਹੀ ਧੁਰੇ ਉੱਤੇ ਘੁੰਮਣ ਨਾਲ ਅਕਾਸ਼ ਵਿੱਚ ਜੋ ਹਿਲ ਜੁਲ ਹੁੰਦੀ ਰਹਿੰਦੀ ਹੈ। ਸੁਭਾਵਿਕ ਹੀ ਇਹ ਫ਼ਰਜ਼ ਕਰਨਾ ਸੌਖਾ ਹੋ ਗਿਆ ਕਿ ਅਚੱਲ ਤਾਰੇ ਸੂਰਜ ਵਰਗੇ ਹੀ ਹਨ ਪਰ ਸਾਥੋਂ ਹੋਰ ਵੀ ਦੂਰ-ਦੁਰਾਡੇ!

ਨਿਊਟਨ ਨੇ ਇਹ ਗੱਲ ਸਮਝ ਲਈ ਸੀ, ਕਿ ਖਿੱਚ ਦੇ ਗੁਰ ਅਨੁਸਾਰ ਤਾਰਿਆਂ ਵਿੱਚ ਆਪਸੀ ਖਿੱਚ ਹੋਣੀ ਜ਼ਰੂਰੀ ਹੈ ਅਤੇ ਐਉਂ ਪ੍ਰਤੀਤ ਹੁੰਦਾ ਸੀ ਕਿ ਤਾਰੇ ਹਿਲਣ ਜੁਲਣ ਤੋਂ ਬਿਨਾਂ ਨਹੀਂ ਰਹਿ ਸਕਦੇ। ਕੀ ਉਹ ਸਾਰੇ ਦੇ ਸਾਰੇ ਕਦੇ ਇਕੱਠੇ ਡਿੱਗ ਪੈਣਗੇ ? ਰਿਚਰਡ ਬੈਂਟਲੀ (Richard Bentley) ਨੇ 1691 ਵਿੱਚ ਲਿਖੇ ਪੱਤਰ ਵਿੱਚ, ਜੋ ਉਸ ਸਮੇਂ ਦਾ ਇਕ ਹੋਰ ਉੱਘਾ ਚਿੰਤਕ ਮੰਨਿਆ ਜਾਂਦਾ ਸੀ। ਇਹ ਦਲੀਲ ਦਿੱਤੀ ਸੀ, ਕਿ ਅਜਿਹਾ ਕੇਵਲ ਉਦੋਂ ਹੋ ਸਕਦਾ ਹੈ, ਜਦੋਂ ਗਿਣਤੀ ਦੇ ਤਾਰੇ ਪੁਲਾੜ ਵਿੱਚ ਇਕ ਸੀਮਤ ਹਿੱਸੇ ਵਿੱਚ ਖਿੰਡੇ ਹੋਏ ਹੋਣ। ਪ੍ਰੰਤੂ ਉਸ ਨੇ ਉਸ ਵੇਲੇ ਇਹ ਸਾਬਤ ਕੀਤਾ ਕਿ ਦੂਜੇ ਬੰਨੇ ਜੇ ਅਣਗਿਣਤ ਤਾਰੇ, ਇਕ ਅਸੀਮਤ ਹਿੱਸੇ ਵਿੱਚ ਬਰਾਬਰ ਖਿੰਡੇ ਹੋਏ ਹੋਣ, ਅਜਿਹਾ ਨਹੀਂ ਹੋ ਸਕਦਾ। (ਭਾਵ ਤਾਰੇ ਸਮੂਹਕ ਤੌਰ ‘ਤੇ ਡਿੱਗ ਨਹੀਂ ਸਕਦੇ!) ਕਿਉਂਕਿ ਉਨ੍ਹਾਂ ਲਈ ਡਿੱਗਣ ਲਈ ਕੋਈ ਕੇਂਦਰ ਬਿੰਦੂ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੋਵੇਗਾ।

ਇਹ ਦਲੀਲ ਉਨ੍ਹਾਂ ਅੜਿਕਿਆਂ ਦੀ ਇਕ ਮਿਸਾਲ ਹੈ, ਜਿਹੜੇ ਅਸੀਮ ਸਥਿਤੀ ਬਾਰੇ ਵਿਚਾਰ ਕਰਨ ਵੇਲੇ ਪੇਸ਼ ਆ ਸਕਦੇ ਹਨ। ਸੀਮਾ-ਰਹਿਤ ਧਰਤੀ ਵਿੱਚ ਤਾਂ ਹਰ ਇਕ ਥਾਂ ਕੇਂਦਰ-ਬਿੰਦੂ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਕਿਉਂਕਿ ਅਜਿਹੇ ਹਰ ਇਕ ਥਾਂ ਦੇ ਹਰ ਇਕ ਪਾਸੇ ਅਣਗਿਣਤ ਤਾਰੇ ਨਜ਼ਰ ਆਉਣਗੇ। ਬਹੁਤ ਸਮਾਂ ਬੀਤਣ ਉਪਰੰਤ ਜਿਹੜੀ ਸਹੀ ਪਹੁੰਚ ਸਮਝ ਵਿੱਚ ਆਈ ਉਹ ਇਹ ਸੀ ਕਿ ਸੀਮਤ ਆਕਾਰ ਬਾਰੇ ਹੀ ਸੋਚਿਆ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਸਾਰੇ ਤਾਰੇ ਇਕ ਦੂਜੇ ਵੱਲ ਖਿੱਚੇ ਜਾਂਦੇ ਹੋਣ ਅਤੇ ਫੇਰ ਇਹ ਵਿਚਾਰਿਆ ਜਾਵੇ ਕਿ ਇਸ ਖਿਤੇ ਤੋਂ ਬਾਹਰ ਹੋਰ ਤਾਰੇ ਤਕਰੀਬਨ ਇਕੋ ਜਿਹੀ ਮਾਤਰਾ ਵਿੱਚ ਵੰਡਣ ਨਾਲ ਕਿਸ ਪ੍ਰਕਾਰ ਦੀ ਤਬਦੀਲੀ ਵਾਪਰੇਗੀ। ਨਿਊਟਨ ਦੇ ਮੱਤ ਅਨੁਸਾਰ ਵਾਧੂ ਤਾਰਿਆਂ ਨਾਲ ਮੁੱਢਲੇ ਤਾਰਿਆਂ ਉੱਤੇ ਕੋਈ ਅਸਰ ਨਹੀਂ ਪਵੇਗਾ ਅਤੇ ਤਾਰੇ ਪੂਰੀ ਤੇਜ਼ ਰਫ਼ਤਾਰ ਨਾਲ ਡਿੱਗ ਪੈਣਗੇ। ਅਸੀਂ ਭਾਵੇਂ ਕਿਤਨੇ ਹੋਰ ਤਾਰੇ ਵਧਾ ਦੇਈਏ, ਪਰੰਤੂ ਉਹ ਸਦਾ ਵਾਂਗ ਇਕ ਦੂਜੇ ਉੱਤੇ ਢਹਿੰਦੇ ਰਹਿਣਗੇ। ਹੁਣ ਸਾਨੂੰ ਇਹ ਪਤਾ ਲੱਗ ਚੁੱਕਾ ਹੈ ਕਿ ਅਸੀਮ ਆਕਾਰ ਵਾਲੀ ਧਰਤੀ ਦਾ ਹੋਣਾ ਅਸੰਭਵ ਹੈ, ਜੋ ਅਚੱਲ ਅਤੇ ਅਹਿਲ ਹੋਵੇ ਅਤੇ ਉਸ ਵਿੱਚ ਚੁੰਬਕ ਸ਼ਕਤੀ ਮੌਜੂਦ ਹੋਵੇ। ਇਹ ਇਕ ਸਾਧਾਰਨ ਜਿਹੀ ਪਰ ਦਿਲਚਸਪ ਵਿਚਾਰਧਾਰਾ ਹੈ ਕਿ ਵੀਹਵੀਂ ਸ਼ਤਾਬਦੀ ਤੋਂ ਪਹਿਲਾਂ ਕਿਸੇ ਨੂੰ ਵੀ ਇਹ ਸੋਝੀ ਨਹੀਂ ਹੋਈ ਸੀ ਕਿ ਧਰਤੀ ਦਾ ਆਕਾਰ ਫੈਲ ਰਿਹਾ ਹੈ ਜਾਂ ਸੁੰਗੜ ਰਿਹਾ ਹੈ। ਆਮ ਵਿਚਾਰ ਇਹ ਸੀ ਕਿ ਜਾਂ ਤਾਂ ਧਰਤੀ ਪਹਿਲਾਂ ਤੋਂ ਹੀ ਵਜੂਦ ਵਿੱਚ ਆਈ ਹੋਈ ਹੈ ਅਤੇ ਇਹ ਅਚੱਲ ਹੈ ਜਾਂ ਇਹ ਕਿਸੇ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਹੋਂਦ ਵਿੱਚ ਲਿਆਂਦੀ ਗਈ ਹੈ, ਜਿਸ ਰੂਪ ਵਿੱਚ ਅਸੀਂ ਇਸ ਨੂੰ ਦੇਖ ਰਹੇ ਹਾਂ। ਇਸ ਵਿਚਾਰ ਦਾ ਅੰਸ਼ਕ ਕਾਰਨ ਇਹ ਸੀ ਕਿ ਲੋਕ ਸਦੀਵੀ ਸੱਚਾਈਆਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ ਅਤੇ ਉਹ ਅਜਿਹਾ ਸੋਚਣ ਵਿੱਚ ਸੌਖ ਮਹਿਸੂਸ ਕਰਦੇ ਸਨ ਕਿ ਭਾਵੇਂ ਉਹ ਬਿਰਧ ਹੋ ਜਾਣਗੇ ਅਤੇ ਮਰ ਵੀ ਜਾਣਗੇ, ਪਰ ਇਹ ਧਰਤੀ ਤਾਂ ਸਦੀਵੀ ਅਮਰ ਰਹਿਣ ਵਾਲੀ ਹੈ ਅਤੇ ਇਸ ਵਿੱਚ ਕੋਈ ਤਬਦੀਲੀ ਨਹੀਂ ਹੋ ਸਕਦੀ।

ਜਿਹੜੇ ਲੋਕ ਤਾਂ ਇਹ ਸਮਝ ਗਏ ਸਨ ਕਿ ਨਿਊਟਨ ਦੇ ਮੱਤ ਅਨੁਸਾਰ, ਧਰਤੀ ਅਚੱਲ ਅਤੇ ਅਹਿਲ ਨਹੀਂ ਹੋ ਸਕਦੀ, ਪਰ ਇਹ ਸੋਚਣ ਲਈ ਤਿਆਰ ਨਹੀਂ ਸਨ ਕਿ ਧਰਤੀ ਦਾ ਆਕਾਰ ਫੈਲ ਰਿਹਾ ਹੈ। ਇਸ ਦੇ ਉਲਟ ਉਨ੍ਹਾਂ ਨੇ ਨਿਊਟਨ ਦੇ ਮੱਤ ਵਿੱਚ ਇਹ ਸੋਧ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਕਿ ਚੁੰਬਕ ਸ਼ਕਤੀ ਦੂਰ ਜਾ ਕੇ ਰੁਕਣ ਲੱਗ ਜਾਂਦੀ ਹੈ ਜਾਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀ ਹੈ। ਅਜਿਹੇ ਵਿਚਾਰ ਨਾਲ, ਉਨ੍ਹਾਂ ਵੱਲੋਂ ਗ੍ਰਹਿ ਦੀ ਹਿੱਲਜੁਲ ਬਾਰੇ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਭਵਿੱਖਬਾਣੀਆਂ ਉੱਤੇ ਕੋਈ ਵੀ ਅਸਰ ਨਾ ਪਿਆ, ਸਗੋਂ ਇਸ ਵਿਚਾਰ ਵਿੱਚ ਇਹ ਸੋਚਣ ਦੀ ਗੁੰਜਾਇਸ਼ ਜ਼ਰੂਰ ਸੀ ਕਿ ਅਣਗਿਣਤ ਤਾਰੇ ਇਕ ਸੰਤੁਲਨ ਵਿੱਚ ਫੈਲੇ ਹੋਏ ਸਨ ਅਤੇ ਇਕ ਦੂਜੇ ਤੋਂ ਨੇੜਲੇ ਤਾਰਿਆਂ ਵਿਚਕਾਰ ਚੁੰਬਕ ਸ਼ਕਤੀ, ਇਕ ਦੂਜੇ ਤੋਂ ਦੁਰੇਡੇ ਤਾਰਿਆਂ ਵਿਚਕਾਰ ਮੱਠੀ ਪੈ ਚੁੱਕੀ ਚੁੰਬਕ ਸ਼ਕਤੀ ਇਕ ਦੂਜੇ ਦੇ ਬਰਾਬਰ ਸੀ। ਪਰੰਤੂ ਹੁਣ ਸਾਨੂੰ ਇਸ ਵਿਸ਼ਵਾਸ ਅਨੁਸਾਰ ਇਸ ਪ੍ਰਕਾਰ ਦਾ ਸੰਤੁਲਨ ਸਥਾਈ ਨਹੀਂ ਹੋ ਸਕਦਾ। ਜੇ ਕਿਸੇ ਖਿੱਤੇ ਵਿੱਚ ਤਾਰੇ ਕੁਝ ਕੁ ਇਕ ਦੂਜੇ ਦੇ ਨੇੜੇ ਹੋ ਜਾਣ, ਤਾਂ ਉਨ੍ਹਾਂ ਵਿਚਕਾਰ ਚੁੰਬਕ ਸ਼ਕਤੀ ਵਧੇਰੇ ਬਲਵਾਨ ਹੋ ਜਾਵੇਗੀ ਅਤੇ ਰੁਕਾਵਟ ਪਾਉਣ ਵਾਲੀ ਸ਼ਕਤੀ ਉਸ ਨੂੰ ਕਮਜ਼ੋਰ ਨਹੀਂ ਕਰ ਸਕੇਗੀ ਅਤੇ ਇਕ ਦੂਜੇ ਦੇ ਹੋਰ ਨੇੜੇ ਹੁੰਦੇ ਜਾਣਗੇ। ਦੂਜੇ ਬੰਨੇ ਜੇ ਤਾਰੇ ਇਕ ਦੂਜੇ ਤੋਂ ਕੁਝ ਦੂਰ ਹੋ ਜਾਣ, ਤਾਂ ਰੁਕਾਵਟ ਪਾਉਣ ਵਾਲੀ ਸ਼ਕਤੀ ਭਾਰੂ ਹੋ ਜਾਵੇਗੀ ਅਤੇ ਤਾਰਿਆਂ ਦੀ ਦੂਰੀ ਵੱਧਦੀ ਰਹੇਗੀ।

ਅਸੀਮ ਆਕਾਰੀ ਧਰਤੀ, ਜੋ ਅਚਲ ਅਤੇ ਅਹਿਲ ਮੰਨੀ ਜਾਂਦੀ ਸੀ ਦਾ ਇਕ ਹੋਰ ਵਿਰੋਧੀ ਵਿਚਾਰ ਜਰਮਨ ਦਾਰਸ਼ਨਿਕ ਹੈਨਰਿਕ ਓਲਬਰਜ਼ (Heinrick Olbers) ਦੇ ਨਾਮ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ, ਜਿਸ ਨੇ ਉਕਤ ਵਿਚਾਰ ਬਾਰੇ 1823 ਈਸਵੀ ਵਿੱਚ ਲਿਖਿਆ ਸੀ। ਵਾਸਤਵ ਵਿੱਚ, ਨਿਊਟਨ ਦੇ ਮੱਤ ਦਾ ਵਿਰੋਧ ਉਸ ਦੇ ਕਈ ਸਮਕਾਲੀ ਕਰ ਚੁੱਕੇ ਸਨ ਅਤੇ ਓਲਬਰਜ਼ ਇਸ ਵਿਚਾਰ ਦੇ ਵਿਰੁੱਧ ਮੰਨਣ ਯੋਗ ਦਲੀਲ ਦੇਣ ਵਾਲਾ ਪਹਿਲਾ ਵਿਅਕਤੀ ਨਹੀਂ ਸੀ। ਪਰੰਤੂ, ਇਹ ਵਿਚਾਰ ਪਹਿਲੀ ਵਾਰ ਵਿਆਪਕ ਤੌਰ ‘ਤੇ ਵਿਚਾਰ ਅਧੀਨ ਆਉਣ ਵਾਲਾ ਪਹਿਲਾ ਵਿਚਾਰ ਸੀ। ਔਕੜ ਤਾਂ ਇਹ ਹੈ ਕਿ ਅਸੀਮ ਆਕਾਰੀ ਅਚੱਲ ਧਰਤੀ ਉੱਤੇ ਸਾਡੀ ਨਜ਼ਰ ਤਾਰੇ ਦੀ ਸਤਹ ਉੱਤੇ ਹੀ ਖ਼ਤਮ ਹੋ ਸਕੇਗੀ। ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਉਮੀਦ ਬੱਝ ਜਾਵੇਗੀ ਕਿ ਸਮੁੱਚੇ ਆਕਾਸ਼ ਵਿੱਚ, ਇੱਥੋਂ ਤੱਕ ਕਿ ਰਾਤ ਦੇ ਸਮੇਂ ਵੀ, ਸੂਰਜ ਵਰਗੀ ਰੌਸ਼ਨੀ ਹੋਵੇਗੀ। ਓਲਬਰਜ਼ ਦੀ ਵਿਰੋਧੀ ਦਲੀਲ ਇਹ ਸੀ ਕਿ ਦੁਰੇਡੇ ਤਾਰਿਆਂ ਦੀ ਰੌਸ਼ਨੀ ਰਸਤੇ ਵਿਚਲੇ ਪਦਾਰਥਾਂ ਸਦਕਾ ਮੱਧਮ ਪੈ ਜਾਵੇਗੀ। ਪਰੰਤੂ ਅਜਿਹਾ ਵਾਪਰਨ ਨਾਲ, ਰਸਤੇ ਵਿਚਲਾ ਪਦਾਰਥ ਉਦੋਂ ਤੱਕ ਤਪਦਾ ਰਹੇਗਾ, ਜਦੋਂ ਤੱਕ ਉਹ ਤਾਰਿਆਂ ਵਾਂਗ ਚਮਕਣ ਨਾ ਲੱਗ ਜਾਵੇ। ਇਸ ਫ਼ੈਸਲੇ ਤੋਂ ਬਚਣ ਲਈ ਕਿ ਰਾਤ ਨੂੰ ਸਮੁੱਚਾ ਆਕਾਸ਼ ਸੂਰਜ ਵਾਂਗ ਚਮਕਣ ਲੱਗ ਸਕਦਾ ਹੈ, ਇਹ ਫ਼ਰਜ਼ ਕਰਨਾ ਪਵੇਗਾ, ਕਿ ਤਾਰੇ ਸਦਾ ਹੀ ਚਮਕਦੇ ਨਹੀਂ ਰਹੇ, ਪਰੰਤੂ ਬੀਤੇ ਹੋਏ ਸਮੇਂ ਵਿੱਚੋਂ, ਕਿਸੇ ਖ਼ਾਸ ਨਿਸ਼ਚਿਤ ਵੇਲੇ ਚਮਕਣ ਲੱਗੇ ਹਨ। ਅਜਿਹੀ ਹਾਲਤ ਵਿੱਚ, ਉਨ੍ਹਾਂ ਦੇ ਰਸਤੇ ਵਿੱਚ ਪਦਾਰਥ ਹਾਲੇ ਤੱਕ ਤਪਿਆ ਹੀ ਨਹੀਂ; ਜਾਂ ਦੁਰੇਡੇ ਤਾਰਿਆਂ ਦੀ ਰੌਸ਼ਨੀ ਹਾਲੇ ਸਾਡੇ ਤੱਕ ਪਹੁੰਚ ਨਹੀਂ ਸਕੀ। ਅਜਿਹਾ ਫ਼ਰਜ਼ ਕਰਨ ਨਾਲ ਇਹ ਪ੍ਰਸ਼ਨ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ਕਿ ਤਾਰਿਆਂ ਵਿੱਚ ਪਹਿਲੀ ਵਾਰ ਚਮਕ ਪੈਦਾ ਹੋਣ ਦਾ ਕਾਰਨ ਕੀ ਹੈ ?

ਧਰਤੀ ਦੇ ਪਹਿਲੀ ਵਾਰ ਹੋਂਦ ਵਿੱਚ ਆਉਣ ਉੱਤੇ, ਪਹਿਲਾਂ ਵੀ ਵਿਚਾਰ ਕੀਤੀ ਜਾਂਦੀ ਰਹੀ ਹੈ—ਕਈ ਪੁਲਾੜੀ ਖੋਜਾਂ ਅਤੇ ਯਹੂਦੀ/ਈਸਾਈ/ਇਸਲਾਮੀ ਪ੍ਰੰਪਰਾਵਾਂ ਅਨੁਸਾਰ, ਚੋਖਾ ਸਮਾਂ ਪਹਿਲਾ ਨਹੀਂ, ਧਰਤੀ ਦਾ ਮੁੱਢ, ਇਕ ਨਿਸ਼ਚਿਤ ਵੇਲੇ ਬੱਝਿਆ ਦੱਸਿਆ ਜਾਂਦਾ ਹੈ। ਧਰਤੀ ਦੇ ਮੁੱਢ ਬਾਰੇ ਇਕ ਦਲੀਲ ਤਾਂ ਇਹ ਸੀ ਕਿ ਇਸ ਦੀ ਰਚਨਾ ਦਾ ਕੋਈ ਨਾ ਕੋਈ ਪਹਿਲਾਂ ਕਾਰਨ ਹੋਣਾ ਜ਼ਰੂਰੀ ਸੀ। (ਦੁਨੀਆਂ ਵਿੱਚ, ਕਿਸੇ ਇਕ ਘਟਨਾ ਦਾ ਕਾਰਣ ਕੋਈ ਹੋਰ ਘਟਨਾ ਦਾ ਵਾਪਰਨਾ ਅਸੀਂ ਜ਼ਰੂਰੀ ਸਮਝਦੇ ਹਾਂ, ਪਰੰਤੂ ਧਰਤੀ ਦੇ ਮੁੱਢ ਸਮੇਂ ਇਹ ਦਲੀਲ ਕੇਵਲ ਉਸ ਹਾਲਤ ਵਿੱਚ ਹੀ ਦਿੱਤੀ ਜਾ ਸਕਦੀ ਹੈ, ਜੇ ਇਸ ਰਚਨਾ ਦਾ ਕੋਈ ਅਰੰਭ ਹੋਇਆ ਹੋਵੇ!) ਇਕ ਹੋਰ ਦਲੀਲ ਸੰਤ ਆਗਸਟੀਨ ਨੇ ਆਪਣੀ ਪੁਸਤਕ (“The City of God’) ‘ਈਸ਼ਵਰ ਦਾ ਨਗਰ’ ਵਿੱਚ ਦਿੱਤੀ ਸੀ। ਉਸ ਨੇ ਦੱਸਿਆ ਕਿ ਸਭਿਅਤਾ ਵਿਕਾਸ ਕਰ ਰਹੀ ਹੈ ਅਤੇ ਸਾਨੂੰ ਚੇਤੇ ਹੈ ਕਿ ਕਿਹੜਾ ਕਾਰਨਾਮਾ ਕਿਸ ਨੇ ਕੀਤਾ ਹੈ ਅਤੇ ਕਿਹੜੀ ਤਕਨੀਕ ਕਿਸ ਨੇ ਵਿਕਸਿਤ ਕੀਤੀ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਮਨੁੱਖ ਹੀ ਨਹੀਂ, ਸਗੋਂ ਇਸ ਧਰਤੀ ਦੀ ਉਮਰ ਬਹੁਤ ਲੰਮੀ ਨਹੀਂ ਹੋ ਸਕਦੀ। ਸੰਤ ਅਗਸਟੀਨ ਨੇ, Genesis ਦੀ ਪੁਸਤਕ ਅਨੁਸਾਰ ਧਰਤੀ ਦਾ ਮੁੱਢ 5000 ਸਾਲ ਪੂਰਬ ਈਸਵੀ ਵਿੱਚ ਬੱਝਿਆ ਦੱਸਿਆ ਹੈ। (ਇਹ ਇਕ ਦਿਲਚਸਪ ਗੱਲ ਹੈ ਕਿ ਅਜਿਹਾ ਮੁੱਢ “ਬਰਫ ਯੁਗ” ਤੋਂ ਬਹੁਤੇ ਫ਼ਰਕ ਨਾਲ ਨਹੀਂ ਹੋਇਆ, ਜੋ 10,000 ਸਾਲ ਪੂਰਬ ਈਸਵੀ ਵਿੱਚ ਸੀ, ਜਦੋਂ ਰੁਤ-ਵਿਗਿਆਨੀਆਂ ਅਨੁਸਾਰ ਸਭਿਅਤਾ ਦਾ ਆਰੰਭ ਹੋਇਆ ਸੀ।)

ਦੂਜੇ ਬੰਨੇ, ਅਰਸਤੂ ਅਤੇ ਯੂਨਾਨ ਦੇ ਜ਼ਿਆਦਾਤਰ ਦਾਰਸ਼ਨਿਕਾਂ ਨੇ, ਧਰਤੀ ਦੇ ਪੈਦਾ ਕਰਨ ਦੇ ਵਿਚਾਰ ਨੂੰ ਅਪਣਾਇਆ ਹੀ ਨਹੀਂ ਸੀ, ਕਿਉਂਕਿ ਅਜਿਹੀ ਹਾਲਤ ਵਿੱਚ, ਈਸ਼ਵਰੀ ਦਖ਼ਲ ਦੀ ਬਹੁਤ ਲੋੜ ਪੈਣੀ ਸੀ। ਇਸ ਲਈ ਉਹ ਸੋਚਦੇ ਸਨ ਮਨੁੱਖ ਮਾਤਰ ਅਤੇ ਇਸ ਦੇ ਦੁਆਲੇ ਫੈਲੀ ਹੋਈ ਧਰਤੀ ਪਹਿਲਾਂ ਤੋਂ ਹੀ ਮੌਜੂਦ ਸੀ, ਸਦਾ ਮੌਜੂਦ ਰਹੇਗੀ। ਪ੍ਰਾਚੀਨ ਲੋਕ ਵਿਕਾਸ ਦੀ ਉੱਪਰ ਦੱਸੀ ਦਲੀਲ ਨੂੰ ਪਹਿਲਾਂ ਮੰਨਦੇ ਆਏ ਸਨ ਅਤੇ ਦਲੀਲ ਦਿੰਦੇ ਸਨ ਕਿ ਸਮੇਂ-ਸਮੇਂ ਸਿਰ ਹੜ੍ਹ ਆਉਂਦੇ ਰਹੇ ਹਨ ਜਾਂ ਹੋਰ ਤਬਾਹੀਆਂ ਹੁੰਦੀਆਂ ਰਹੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੇ ਵਾਰ-ਵਾਰ ਵਾਪਰਨ ਨਾਲ ਮਨੁੱਖੀ ਸਮਾਜ ਵਿੱਚ ਸਭਿਅਤਾ ਮੁੜ-ਮੁੜ ਅਰੰਭ ਹੁੰਦੀ ਰਹੀ ਹੈ।

ਇਨ੍ਹਾਂ ਪ੍ਰਸ਼ਨਾਂ ਦੀ ਨਿਰਖ ਪਿੱਛੋਂ ਜਾ ਕੇ Immanuel Kant ਦਾਰਸ਼ਨਿਕ ਨੇ ਵੇਰਵੇ ਸਹਿਤ ਕੀਤੀ ਸੀ ਕਿ ਧਰਤੀ ਦਾ ਕੋਈ ਮੁੱਢ ਹੈ ਅਤੇ ਕੀ ਇਸ ਦਾ ਆਕਾਰ ਸੀਮਾਬੱਧ •ਹੈ? ਅਜਿਹੀ ਨਿਰਖ ਉਸ ਦੀ ਪ੍ਰਸਿੱਧ (ਪਰ ਅਣਗੋਲੀ) ਪੁਸਤਕ ‘eritique of the Reason’ ਵਿੱਚ ਲਿਖੀ ਸੀ, ਜੋ 1781 ਈਸਵੀ ਵਿੱਚ ਪ੍ਰਕਾਸ਼ਤ ਹੋਈ ਸੀ। ਉਸ ਨੇ ਲਿਖਿਆ ਸੀ ਕਿ ਇਹ ਪ੍ਰਸ਼ਨ ਕਿਸੇ ਸਿੱਟੇ ਉੱਤੇ ਪਹੁੰਚਣ ਵਿੱਚ ਸਵੈ-ਵਿਰੋਧੀ ਹਨ, ਕਿਉਂਕਿ ਉਸ ਨੂੰ ਮਹਿਸੂਸ ਹੋਇਆ ਕਿ ਇਨ੍ਹਾਂ ਪ੍ਰਸ਼ਨਾਂ ਦੁਆਰਾ ਇਹ ਵਿਸ਼ਵਾਸ ਵੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਧਰਤੀ ਦਾ ਅਰੰਭ ਹੋਇਆ ਹੈ ਅਤੇ ਇਸ ਦੇ ਉਲਟ ਇਹ ਵੀ ਦਲੀਲ ਦਿੱਤੀ ਜਾ ਸਕਦੀ ਹੈ ਕਿ ਧਰਤੀ ਸਦਾ ਤੋਂ ਹੀ ਮੌਜੂਦ ਚਲੀ ਆਈ ਹੈ। ਪਹਿਲੇ ਮੱਤ ਦੇ ਹੱਕ ਵਿੱਚ ਇਹ ਦਲੀਲ ਦਿੱਤੀ ਜਾ ਸਕਦੀ ਹੈ ਕਿ ਜੇ ਧਰਤੀ ਦਾ ਕਦੇ ਵੀ ਅਰੰਭ ਨਹੀਂ ਹੋਇਆ ਤਾਂ ਕਿਸੇ ਵੀ ਘਟਨਾ ਦੇ ਵਾਪਰਨ ਤੋਂ ਪਹਿਲਾਂ ਸੀਮਾ-ਰਹਿਤ ਸਮਾਂ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਜਿਸ ਨੂੰ ਉਹ ਬੇਹੂਦਾ ਗੱਲ ਸਮਝਦਾ ਹੈ। ਦੂਜੇ ਮੱਤ ਦੇ ਹੱਕ ਵਿੱਚ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਜੇ ਧਰਤੀ ਦਾ ਕਦੇ ਨਾ ਕਦੇ ਅਰੰਭ ਜ਼ਰੂਰ ਹੋਇਆ ਹੈ ਤਾਂ ਉਸ ਤੋਂ ਪਹਿਲਾਂ ਬੀਤ ਚੁੱਕੇ ਸਮੇਂ ਦੀ ਕੋਈ ਸੀਮਾ ਨਹੀਂ ਹੋ ਸਕਦੀ ਤਾਂ ਫੇਰ ਧਰਤੀ ਦਾ ਅਰੰਭ ਕਿਸੇ ਇਕ ਵਿਸ਼ੇਸ਼ ਸਮੇਂ ਹੋਣਾ ਕਿਉਂ ਮੰਨਿਆ ਜਾਵੇ ? ਅਸਲ ਵਿੱਚ ਉਸ ਦੇ ਹਾਂ-ਪੱਖੀ ਅਤੇ ਨਾਂਹ-ਪੱਖੀ ਮੱਤਾਂ ਵਿੱਚ ਇੱਕੋ ਜਿਹੀਆਂ ਦਲੀਲਾਂ ਪ੍ਰਗਟ ਹੁੰਦੀਆਂ ਹਨ। ਉਸ ਦੇ ਦੋਹਾਂ ਮੱਤਾਂ ਦਾ ਆਧਾਰ ਉਸ ਦੀ ਫ਼ਰਜ਼ੀ ਕਲਪਨਾ ਹੈ ਕਿ ਸਮਾਂ ਤਾਂ ਸਦਾ ਹੀ ਮੌਜੂਦ ਚਲਿਆ ਆਉਂਦਾ ਹੈ, ਧਰਤੀ ਭਾਵੇਂ ਸਦਾ ਤੋਂ ਮੌਜੂਦ ਸਮਝ ਲਈ ਜਾਵੇ ਜਾਂ ਨਾ ਸਮਝ ਲਈ ਜਾਵੇ। ਕਿਉਂਕਿ ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਧਰਤੀ ਦਾ ਅਰੰਭ ਹੋਣ ਤੋਂ ਪਹਿਲੇ ਸਮੇਂ ਦੀ ਕੋਈ ਤੁਕ ਨਹੀਂ ਬਣਦੀ। ਇਹ ਵਿਚਾਰ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਸੰਤ ਅਗਸਤੀਨ ਨੇ ਪ੍ਰਗਟ ਕੀਤਾ ਸੀ। ਜਦੋਂ ਉਸ ਨੂੰ ਪੁੱਛਿਆ ਗਿਆ, “ਧਰਤੀ ਦੀ ਰਚਨਾ ਤੋਂ ਪਹਿਲਾਂ ਈਸ਼ਵਰ ਕੀ ਕਰਦਾ ਸੀ ?” ਅਗਸਤੀਨ ਨੇ ਕੋਈ ਉੱਤਰ ਨਹੀਂ ਸੀ ਦਿੱਤਾ। ਉਹ ਤਾਂ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪ੍ਰਸ਼ਨ ਕਰਨ ਵਾਲਿਆਂ ਲਈ ਨਰਕ ਦੀ ਤਿਆਰੀ ਕਰ ਰਿਹਾ ਸੀ। ਇਸ ਦੇ ਉਲਟ ਉਸ ਨੇ ਕਿਹਾ ਕਿ ਸਮਾਂ ਉਸ ਧਰਤੀ ਦੀ ਜ਼ਾਇਦਾਦ ਹੈ, ਜਿਸ ਨੂੰ ਈਸ਼ਵਰ ਨੇ ਰਚਿਆ ਹੈ ਅਤੇ ਉਹ ਸਮਾਂ ਧਰਤੀ ਦੇ ਅਰੰਭ ਤੋਂ ਪਹਿਲਾਂ ਮੌਜੂਦ ਹੀ ਨਹੀਂ ਸੀ।

ਜਦੋਂ ਬਹੁਤੇ ਲੋਕਾਂ ਦਾ ਇਹ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਧਰਤੀ ਅਚੱਲ ਅਤੇ ਤਬਦੀਲੀ ਤੋਂ ਮੁਕਤ ਹੈ, ਤਾਂ ਉਸ ਵੇਲੇ ਇਹ ਪ੍ਰਸ਼ਨ ਕਰਨਾ ਕਿ ਇਸ ਦਾ ਕਦੇ ਅਰੰਭ ਹੋਇਆ ਹੈ ਜਾਂ ਨਹੀਂ। ਇਕ ਥੋਥਾ ਵਿਚਾਰ ਸੀ ਜਾਂ ਧਾਰਮਿਕ ਅੰਧ-ਵਿਸ਼ਵਾਸ। ਦੋਹਾਂ ਹਾਲਤਾਂ ਵਿੱਚ ਐਉਂ ਜਾਪਦਾ ਹੈ ਕਿ ਧਰਤੀ ਸਦਾ ਤੋਂ ਹੀ ਮੌਜੂਦ ਚਲੀ ਆਉਂਦੀ ਹੈ ਜਾਂ ਇਸ ਦੀ ਰਚਨਾ ਕਿਸੇ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਇਸ ਢੰਗ ਨਾਲ ਕੀਤੀ ਗਈ ਹੈ ਕਿ ਦੇਖਣ ਵਾਲੇ ਨੂੰ ਐਉਂ ਜਾਪੇ ਕਿ ਇਹ ਸਦਾ ਤੋਂ ਹੀ ਮੌਜੂਦ ਚਲੀ ਆਈ ਹੈ। ਪਰੰਤੂ 1929 ਵਿੱਚ, ਐਡਵਿਨ ਹੁਬਲ (Edwin Hubble) ਨੇ ਇਕ ਅਤੀ ਠੋਸ ਵਿਚਾਰ ਪੇਸ਼ ਕੀਤਾ ਸੀ ਕਿ ਤੁਸੀਂ ਕਿਸੇ ਪਾਸੇ ਦੇਖ ਲਓ, ਪੁਲਾੜੀਂ ਮੰਡਲ ਬੜੀ ਤੇਜ਼ੀ ਨਾਲ ਸਾਥੋਂ ਦੂਰ ਜਾ ਰਹੇ ਹਨ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਇਹ ਸਮਝ ਲਓ ਕਿ ਧਰਤੀ ਫੈਲ ਰਹੀ ਹੈ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਪਹਿਲੇ ਸਮਿਆਂ ਵਿੱਚ, ਇਹ ਮੰਡਲ ਇਕ ਦੂਜੇ ਦੇ ਨੇੜੇ-ਨੇੜੇ ਹੁੰਦੇ ਸਨ, ਭਾਵ ਇਕ ਜਾਂ ਦੋ

ਅਰਬ ਸਾਲ ਪਹਿਲਾਂ। ਉਹ ਸਾਰੇ ਦੇ ਸਾਰੇ ਮੰਡਲ ਇਕੋ ਥਾਂ ਹੁੰਦੇ ਸਨ ਅਤੇ ਇਸ ਲਈ ਧਰਤੀ ਦਾ ਆਕਾਰ ਸੀਮਾ-ਰਹਿਤ ਸੀ। ਇਸ ਖੋਜ ਨੇ ਧਰਤੀ ਦੇ ਅਰੰਭ ਹੋਣ ਵਾਲੇ ਪ੍ਰਸ਼ਨ ਨੂੰ ਆਖ਼ਰ ਵਿਗਿਆਨ ਦੇ ਘੇਰੇ ਵਿੱਚ ਪ੍ਰਵੇਸ਼ ਕਰ ਦਿੱਤਾ।

ਹੁੱਬਲ ਦੀ ਖੋਜ ਨੇ ਸੁਝਾਇਆ ਕਿ ਇਕ ਅਜਿਹਾ ਸਮਾਂ ਸੀ, ਜਿਸ ਨੂੰ Big Bang (ਮਹਾਨ ਧਮਾਕਾ) ਕਹਿੰਦੇ ਹਨ, ਜਦੋਂ ਧਰਤੀ ਦਾ ਆਕਾਰ ਅਤਿਅੰਤ ਛੋਟਾ ਜਿਹਾ ਹੁੰਦਾ ਸੀ। ਅਜਿਹੀ ਸਥਿਤੀ ਵਿੱਚ, ਵਿਗਿਆਨ ਦੇ ਸਾਰੇ ਨਿਯਮ, ਅਤੇ ਇਸ ਲਈ, ਭਵਿੱਖ ਦਾ ਅਨੁਮਾਨ ਲਾਉਣ ਵਾਲੀ ਸੂਝ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀ ਹੈ, ਜੇ ਉਸ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਵੀ ਕੁਝ ਘਟਨਾਵਾਂ ਵਾਪਰੀਆਂ ਹੋਣ, ਤਾਂ ਉਨ੍ਹਾਂ ਨਾਲ ਇਸ ਵੇਲੇ ਜੋ ਕੁਝ ਵਾਪਰ ਰਿਹਾ ਹੈ, ਕੋਈ ਅਸਰ ਨਹੀਂ ਪੈ ਸਕਦਾ। ਉਨ੍ਹਾਂ ਦੇ ਵਜੂਦ ਨੂੰ ਅਣਗੌਲਿਆਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਕਿਉਂਕਿ ਕੁਝ ਵੀ ਦੇਖਿਆ ਹੀ ਨਹੀਂ ਜਾ ਸਕਦਾ। ਇਹ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਮਹਾਨ ਧਮਾਕੇ ਤੋਂ ਹੀ ਸਮਾਂ ਆਰੰਭ ਹੁੰਦਾ ਹੈ; ਕਿਉਂਕਿ ਉਸ ਤੋਂ ਪਹਿਲੇ ਸਮੇਂ ਦਾ ਕੋਈ ਵੀ ਨਿਰਣਾ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ। ਇਸ ਗੱਲ ਉੱਤੇ ਜ਼ੋਰ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਸਮੇਂ ਦਾ ਇਹ ਅਰੰਭ ਉਨ੍ਹਾਂ ਵਿਚਾਰਾਂ ਨਾਲੋਂ ਵੱਖਰਾ ਹੈ, ਜੇ ਪਹਿਲਾਂ ਸਮਝੇ ਜਾਂਦੇ ਸਨ। ਤਬਦੀਲੀ ਰਹਿਤ ਧਰਤੀ ਉੱਤੇ, ਸਮੇਂ ਦਾ ਅਰੰਭ, ਧਰਤੀ ਤੋਂ ਬਾਹਰਲੀ ਕਿਸੇ ਸ਼ਕਤੀ ਵੱਲੋਂ ਨਿਸ਼ਚਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਉਂਜ ਅਜਿਹੇ ਅਰੰਭ ਦੀ ਲੋੜ ਹੀ ਨਹੀਂ ਹੈ। ਇਹ ਕਲਪਨਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਕਿ ਈਸ਼ਵਰ ਨੇ ਬੀਤੇ ਸਮੇਂ ਵਿੱਚ ਕਿਸੇ ਨਾ ਕਿਸੇ ਵੇਲੇ, ਧਰਤੀ ਦੀ ਰਚਨਾ ਕੀਤੀ ਹੋਵੇਗੀ। ਦੂਜੇ ਬੰਨੇ, ਜੇ ਧਰਤੀ ਫੈਲ ਰਹੀ ਹੈ ਤਾਂ ਧਰਤੀ ਦੀ ਰਚਨਾ ਕਰਨ ਦੀ ਕੋਈ ਲੋੜ ਹੀ ਨਹੀਂ ਸੀ। ਫੇਰ ਵੀ ਇਹ ਕਲਪਨਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਕਿ ਈਸ਼ਵਰ ਨੇ ਧਰਤੀ ਦੀ ਰਚਨਾ ਮਹਾਨ ਧਮਾਕਾ ਹੋਣ ਸਾਰ ਹੀ ਕਰ ਦਿੱਤੀ ਸੀ। ਜਾਂ ਉਸ ਤੋਂ ਕੁਝ ਚਿਰ ਮਗਰੋਂ ਕੀਤੀ ਹੋਵੇਗੀ ਅਤੇ ਮਹਾਨ ਧਮਾਕਾ ਐਨ ਉਸੇ ਵੇਲੇ ਹੋਇਆ ਸੀ, ਪਰੰਤੂ ਇਸ ਗੱਲ ਦੀ ਕੋਈ ਤੁਕ ਨਹੀਂ ਬਣਦੀ ਕਿ ਧਰਤੀ ਦੀ ਰਚਨਾ ਧਮਾਕੇ ਤੋਂ ਪਹਿਲਾਂ ਕਰ ਦਿੱਤੀ ਹੋਵੇਗੀ। ਫੈਲਣ ਵਾਲੀ ਧਰਤੀ ਲਈ ਕਿਸੇ ਰਚਨਹਾਰ ਦੀ ਲੋੜ ਨਹੀਂ ਸੀ, ਸਗੋਂ ਇਸ ਨਾਲ ਅਜਿਹੀ ਰਚਨਾ ਕਰਨ ਦੇ ਕਾਰਜ ਨੂੰ ਸਮਾਂ-ਬੱਧ ਜ਼ਰੂਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।

ਧਰਤੀ ਦੇ ਸੁਭਾਅ ਬਾਰੇ ਵਿਚਾਰ ਕਰਨ ਲਈ ਅਤੇ ਅਜਿਹੇ ਪ੍ਰਸ਼ਨਾਂ ਦੀ ਚਰਚਾ ਕਰਨ ਲਈ ਕਿ ਇਸ ਦਾ ਕੋਈ ਅਰੰਭ ਵੀ ਹੋਇਆ ਹੈ ਜਾਂ ਨਹੀਂ। ਤੁਹਾਨੂੰ ਇਸ ਗੱਲ ਬਾਰੇ ਸਪੱਸ਼ਟ ਹੋਣਾ ਪਵੇਗਾ ਕਿ ਵਿਗਿਆਨਕ ਮੱਤ ਕੀ ਹੈ ? ਮੈਂ ਤਾਂ ਸਾਧਾਰਣ ਜਿਹਾ ਵਿਚਾਰ ਰੱਖਦਾ ਹਾਂ ਕਿ ਇਸ ਮੱਤ ਅਨੁਸਾਰ ਤਾਂ ਧਰਤੀ ਦਾ ਨਮੂਨਾ ਹੀ ਸਾਹਮਣੇ ਆਵੇਗਾ, ਜਾਂ ਇਸ ਦਾ ਇਕ ਛੋਟਾ ਜਿਹਾ ਹਿੱਸਾ ਅਤੇ ਕੁਝ ਨਿਯਮ, ਜਿਨ੍ਹਾਂ ਦਾ ਸੰਬੰਧ ਧਰਤੀ ਦੇ ਨਮੂਨੇ ਵਿੱਚ ਨਜ਼ਰ ਆਉਣ ਵਾਲੀਆਂ ਪਦਾਰਥਕ ਮਾਤਰਾਵਾਂ ਅਨੁਭਵ ਹੋਣਗੀਆਂ। ਅਜਿਹੀ ਧਰਤੀ ਦਾ ਵਜੂਦ ਸਾਡੇ ਮਨਾਂ ਵਿੱਚ ਹੀ ਹੋਵੇਗਾ ਅਤੇ ਅਜਿਹੇ ਵਜੂਦ ਦੀ ਹੋਰ ਕੋਈ ਅਸਲੀਅਤ ਨਹੀਂ ਹੋਵੇਗੀ (ਉਸ ਦਾ ਅਰਥ ਕੁਝ ਵੀ ਹੋਵੇ) ? ਉਹ ਮੱਤ ਚੰਗਾ ਮੱਤ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਦੋ ਲੋੜਾਂ ਦੀ ਪੂਰਤੀ ਹੁੰਦੀ ਹੋਵੇ। ਇਸ ਵਿੱਚ ਧਰਤੀ ਦੇ ਅਜਿਹੇ ਨਮੂਨੇ ਵਿੱਚ ਉਨ੍ਹਾਂ ਬਹੁਤ ਸਾਰੇ ਨਜ਼ਾਰਿਆਂ ਦਾ ਸਹੀ-ਸਹੀ ਜ਼ਿਕਰ ਹੋਵੇ, ਜਿਸ ਵਿੱਚ ਥੋੜ੍ਹੇ ਜਿਹੇ ਕਲਪਿਤ ਤੱਤ ਹੀ ਮੌਜੂਦ ਹੋਣ ਅਤੇ ਇਹ ਭਵਿੱਖੀ ਨਜ਼ਾਰਿਆਂ ਦੇ ਸਿੱਟਿਆਂ ਬਾਰੇ ਸਹੀ-ਸਹੀ ਭਵਿੱਖਬਾਣੀ ਕਰਦਾ ਹੋਵੇ। ਉਦਾਹਰਣ ਵਜੋਂ, ਅਰਸਤੂ ਦਾ ਮੱਤ ਸੀ ਕਿ ਹਰ ਇਕ ਵਸਤੂ ਚਾਰ ਤੱਤਾਂ ਦੀ ਬਣੀ ਹੋਈ ਹੁੰਦੀ ਹੈ, ਭਾਵ ਮਿੱਟੀ, ਹਵਾ, ਅਗਨੀ ਅਤੇ ਪਾਣੀ। ਇਹ ਮੱਤ ਪ੍ਰਵਾਨ ਤਾਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਪਰੰਤੂ ਇਹ ਸਹੀ-ਸਹੀ ਭਵਿੱਖਬਾਣੀਆਂ ਨਹੀਂ ਕਰਦਾ। ਦੂਜੇ ਬੰਨ੍ਹੇ ਨਿਊਟਨ ਦਾ ਮੱਤ ਚੁੰਬਕ ਖਿੱਚ ਉੱਤੇ, ਇਕ ਸਾਧਾਰਣ ਨਮੂਨੇ ਮਾਤਰ, ਆਧਾਰਿਤ ਸੀ, ਜਿਸ ਅਨੁਸਾਰ ਧਰਤੀਆਂ ਆਪਣੇ-ਆਪਣੇ ਆਕਾਰ ਅਨੁਸਾਰ ਇਕ ਦੂਜੀ ਨੂੰ ਆਪਣੇ ਵੱਲ ਖਿੱਚ ਪਾਉਂਦੀਆਂ ਸਨ। ਜੋ ਦੂਰੀ ਦੇ ਅਨੁਪਾਤ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਸੀ। ਫੇਰ ਵੀ ਇਸ ਮੱਤ ਸਦਕਾ ਸੂਰਜ, ਚੰਦ ਅਤੇ ਹੋਰ ਗ੍ਰਹਿ ਦੀ ਚਾਲ ਅਤੇ ਗਤੀ ਦਾ ਬਹੁਤ ਹੀ ਸਹੀ-ਸਹੀ ਪਤਾ ਲੱਗ ਸਕਦਾ ਸੀ।

ਹਰ ਇਕ ਪਦਾਰਥਕ ਮੱਤ, ਸਦਾ ਹੀ ਕੱਚਾ-ਪਿੱਲਾ ਹੀ ਹੋਇਆ ਕਰਦਾ ਹੈ। ਅਰਥਾਤ ਇਕ ਫ਼ਰਜ਼ਕਾਰੀ ਹੀ, ਜਿਸ ਨੂੰ ਸਾਬਤ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ। ਕਿਸੇ ਮੱਤ ਨਾਲ ਭਾਵੇਂ ਕਿੰਨੇ ਹੀ ਤਜਰਬਿਆਂ ਦੇ ਸਿੱਟੇ ਮੇਲ ਖਾਂਦੇ ਹੋਣ, ਸਾਨੂੰ ਇਸ ਗੱਲ ਦਾ ਪੱਕਾ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਹੋ ਸਕਦਾ। ਕੋਈ ਭਵਿੱਖੀ ਤਜਰਬਿਆਂ ਦਾ ਨਤੀਜਾ ਉਸ ਮੱਤ ਦੇ ਵਿਰੁੱਧ ਨਹੀਂ ਹੋਵੇਗਾ। ਦੂਜੇ ਬੰਨੇ, ਜੇ ਤੁਹਾਨੂੰ ਉਸ ਮੱਤ ਦੇ ਜ਼ਾਹਰਾ ਨਤੀਜਿਆਂ ਦੇ ਵਿਰੁੱਧ ਇਕ ਵੀ ਨਤੀਜਾ ਸਾਹਮਣੇ ਆ ਜਾਵੇ, ਤਾਂ ਤੁਸੀਂ ਉਸ ਮੱਤ ਨੂੰ ਰੱਦ ਕਰ ਸਕਦੇ ਹੋ। ਵਿਗਿਆਨਕ ਦਾਰਸ਼ਨਿਕ ਕਾਰਲ ਪੌਪਰ (Karl Popper) ਅਨੁਸਾਰ ਉਹ ਮੱਤ ਚੰਗਾ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ। ਜਿਹੜਾ ਕਈ ਪੜਤਾਲਾਂ ਕਰਦਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਜ਼ਾਹਰਾ ਨਤੀਜਿਆਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਗ਼ਲਤ ਸਾਬਤ ਕੀਤਾ ਜਾ ਸਕੇ ਅਤੇ ਜਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਝੂਠਾ ਸਾਬਤ ਕੀਤਾ ਜਾ ਸਕੇ। ਜਦੋਂ ਤੱਕ ਪ੍ਰਤੱਖ ਨਤੀਜੇ ਕਿਸੇ ਮੱਤ ਨਾਲ ਮੇਲ ਖਾਂਦੇ ਰਹਿੰਦੇ ਹਨ, ਉਹ ਮੱਤ ਕਾਇਮ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਸਾਡਾ ਵਿਸ਼ਵਾਸ ਉਸ ਮੱਤ ਪ੍ਰਤੀ ਪਕੇਰਾ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ; ਪਰੰਤੂ ਜਦੋਂ ਵੀ ਕੋਈ ਇਕ ਵੀ ਪ੍ਰਤੱਖ ਨਤੀਜਾ ਉਸ ਮੱਤ ਦੇ ਵਿਰੁੱਧ ਪ੍ਰਤੀਤ ਹੋ ਜਾਵੇ, ਤਾਂ ਅਸੀਂ ਉਸ ਮੱਤ ਨੂੰ ਤਿਆਗ ਦਿੰਦੇ ਹਾਂ, ਜਾਂ ਉਸ ਨੂੰ ਸੋਧ ਲੈਂਦੇ ਹਾਂ। ਅਜਿਹਾ ਕੁਝ ਸੁਭਾਵਿਕ ਹੀ ਵਾਪਰਦਾ ਰਹਿੰਦਾ ਹੈ, ਪਰੰਤੂ ਤੁਸੀਂ ਤਜਰਬਾ ਕਰਨ ਵਾਲੇ ਦੀ ਯੋਗਤਾ ਬਾਰੇ ਸਦਾ ਹੀ ਕਿੰਤੂ ਤਾਂ ਕਰ ਹੀ ਸਕਦੇ ਹੋ।

ਅਮਲੀ ਤੌਰ ‘ਤੇ ਐਉਂ ਹੁੰਦਾ ਹੈ ਕਿ ਹਰ ਇਕ ਨਵਾਂ ਮੱਤ, ਅਸਲ ਵਿੱਚ ਪਹਿਲੇ ਮੱਤਾਂ ਦਾ ਹੀ ਵਿਸਥਾਰ ਹੋਇਆ ਕਰਦਾ ਹੈ। ਉਦਾਹਰਣ ਵਜੋਂ, ਮਰਕਰੀ ਗ੍ਰਹਿ ਦੀ ਸਹੀ ਸਹੀ ਖੋਜ ਕਰਨ ਨਾਲ ਨਿਊਟਨ ਦੀ ਚੁੰਬਕ ਸ਼ਕਤੀ ਦੇ ਸਿੱਟਿਆਂ ਵਿੱਚ ਮਾਮੂਲੀ ਜਿਹਾ, ਅੰਤਰ ਮਹਿਸੂਸ ਹੋਇਆ ਕਿ ਉਸ ਦੀ ਚਾਲ ਬਾਰੇ ਸਹੀ ਨਤੀਜਾ ਨਹੀਂ ਸੀ ਨਿਕਲਿਆ। ਅਸਲ ਗੱਲ ਇਹ ਹੈ ਕਿ ਆਈਨ ਸਟਾਈਨ ਦੀ ਮਾਰ੍ਕ ਖੋਜ ਅਨੁਸਾਰ ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਨਿਊਟਨ ਦੀ ਖੋਜ ਨਾਲੋਂ ਵੱਖਰੀ ਸੀ। ਆਈਨ ਸਟਾਈਨ ਨੇ ਜੋ ਕੁਝ ਦੱਸਿਆ ਸੀ, ਉਹੀ ਕੁਝ ਪ੍ਰਤੱਖ ਨਜ਼ਰ ਆਉਂਦਾ ਸੀ। ਨਿਊਟਨ ਦੀ ਖੋਜ ਵਿਚ ਅਜਿਹਾ ਨਹੀਂ ਸੀ। ਇਸ ਤਰ੍ਹਾਂ ਨਵੇਂ ਮੱਤ ਦੀ ਪੁਸ਼ਟੀ ਹੋ ਗਈ ਸੀ। ਪਰ ਫੇਰ ਵੀ ਅਸੀਂ ਨਿਊਟਨ ਦੇ ਮੱਤ ਨੂੰ ਹੀ ਵਧੇਰੇ ਪ੍ਰਵਾਨ ਕਰਦੇ ਹਾਂ, ਕਿਉਂਕਿ ਉਨ੍ਹਾਂ ਦੋਹਾਂ ਦੇ ਨਤੀਜਿਆਂ ਵਿੱਚੋਂ ਬਹੁਰ ਥੋੜ੍ਹਾ ਅੰਤਰ ਹੈ। ਇਸ ਤੋਂ ਇਲਾਵਾ, ਨਿਊਟਨ ਦਾ ਮੱਤ, ਆਈਨ ਸਟਾਈਨ ਦੇ ਮੱਰ ਨਾਲੋਂ ਬਹੁਤ ਸਰਲ ਅਤੇ ਸੌਖਾ ਵੀ ਹੈ।

ਵਿਗਿਆਨ ਦਾ ਅਸਲੀ ਮਨੋਰਥ ਤਾਂ ਅਜਿਹਾ ਗੁਰ ਲੱਭਣਾ ਹੈ, ਜਿਹੜਾ ਸਮੁੱਚੇ ਬ੍ਰਹਿਮੰਡ ਦੀ ਵਿਆਖਿਆ ਕਰਦਾ ਹੋਵੇ। ਪਰੰਤੂ ਬਹੁਤੇ ਵਿਗਿਆਨੀ ਇਸ ਸਮੱਸਿਆ ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਣਾ ਚਾਹੁੰਦੇ ਹਨ। ਪਹਿਲੇ ਭਾਗ ਵਿੱਚ ਤਾਂ ਉਹ ਨਿਯਮ ਆਉਂਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਇਹ ਧਰਤੀ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਕਿਵੇਂ ਬਦਲਦੀ ਰਹਿੰਦੀ ਹੈ। (ਜੇ ਸ਼ਾਨੂੰ ਪਤਾ ਲੱਗ ਜਾਵੇ ਕਿ ਕਿਸੇ ਇਕ ਸਮੇਂ ਧਰਤੀ ਕਿਸ ਪ੍ਰਕਾਰ ਦੀ ਹੈ, ਤਾਂ ਇਨ੍ਹਾਂ, ਨਿਯਮਾਂ ਤੋਂ ਸਾਨੂੰ ਇਹ ਵੀ ਪਤਾ ਲੱਗ ਸਕਦਾ ਹੈ ਕਿ ਕਿਸੇ ਆਉਣ ਵਾਲੇ ਸਮੇਂ ਧਰਤੀ ਦਾ ਕੀ ਰੂਪ ਹੋਵੇਗਾ ? ਦੂਜੇ ਭਾਗ ਵਿੱਚ ਪ੍ਰਸ਼ਨ ਉੱਠਦਾ ਹੈ ਕਿ ਸ਼ੁਰੂ-ਸ਼ੁਰੂ ਵਿੱਚ ਧਰਤੀ ਦੀ ਹਾਲਤ ਕਿਸ ਪ੍ਰਕਾਰ ਦੀ ਸੀ ? ਕੁਝ ਲੋਕ ਮਹਿਸੂਸ ਕਰਦੇ ਹਨ ਕਿ ਵਿਗਿਆਨ ਦਾ ਸੰਬੰਧ ਪਹਿਲੇ ਭਾਗ ਨਾਲ ਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਧਰਤੀ ਦੇ ਅਰੰਭਕ ਪ੍ਰਸ਼ਨ ਨੂੰ ਤਾਂ ਉਹ ਨਿਰਜਿੰਦ ਗੱਲ ਸਮਝਦੇ ਹਨ, ਜਾਂ ਇਕ ਧਾਰਮਿਕ ਵਿਸ਼ਵਾਸ। ਉਹ ਕਹਿੰਦੇ ਹਨ ਕਿ ਈਸ਼ਵਰ ਸਰਬ-ਸ਼ਕਤੀਮਾਨ ਹੋਣ ਕਰਕੇ, ਉਸ ਨੇ ਧਰਤੀ ਦਾ ਅਜਿਹਾ ਮੁੱਢ ਬੰਨ੍ਹਿਆ ਹੋਵੇਗਾ, ਜਿਵੇਂ ਉਸ ਨੂੰ ਚੰਗਾ ਹੀ ਲੱਗਿਆ ਹੋਵੇਗਾ। ਅਜਿਹਾ ਵੀ ਹੋ ਸਕਦਾ ਹੈ, ਕਿ ਉਸ ਨੇ ਧਰਤੀ ਦਾ ਵਿਕਾਸ ਆਪਣੀ ਮਨ-ਮਰਜ਼ੀ ਅਨੁਸਾਰ ਹੀ ਕੀਤਾ ਹੋਵੇਗਾ। ਫੇਰ ਵੀ ਐਉਂ ਪ੍ਰਤੀਤ ਹੁੰਦਾ ਹੈ ਕਿ ਉਸ ਨੇ ਧਰਤੀ ਦਾ ਸਹਿਜੇ-ਸਹਿਜੇ ਵਿਕਾਸ ਕੁਝ ਖ਼ਾਸ ਨਿਯਮਾਂ ਅਨੁਸਾਰ ਹੁੰਦੇ ਰਹਿਣ ਦੀ ਵਿਉਂਤ ਬਣਾਈ ਹੋਵੇਗੀ। ਫੇਰ ਤਾਂ ਜਾਪਦਾ ਹੈ ਕਿ ਧਰਤੀ ਦੇ ਅਰੰਭ ਹੋਣ ਵੇਲੇ ਇਸ ਦੇ ਰੂਪ ਦੇ ਵੀ ਕੁਝ ਖ਼ਾਸ ਨਿਯਮ ਜ਼ਰੂਰ ਹੋਣਗੇ।

ਇਹ ਗੱਲ ਅਤਿ ਕਠਿਨ ਜਾਪਦੀ ਹੈ ਕਿ ਕੋਈ ਅਜਿਹਾ ਗੁਰ ਲੱਭਿਆ ਜਾਵੇ, ਜਿਹੜਾ ਧਰਤੀ ਦੀ ਵਿਆਖਿਆ ਇਕੋ ਵਾਰ ਕਰ ਸਕੇ। ਇਸ ਦੇ ਉਲਟ, ਅਸੀਂ ਇਸ ਸਮੱਸਿਆ ਨੂੰ ਕਈ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡ ਲੈਂਦੇ ਹਾਂ ਅਤੇ ਕਈ ਛੋਟੇ-ਛੋਟੇ ਗੁਰ ਘੜ ਲੈਂਦੇ ਹਾਂ? ਹਰ ਇਕ ਅੰਸ਼ਕ ਗੁਰ ਕੁਝ ਸੀਮਤ ਪ੍ਰਤੱਖ ਨਤੀਜਿਆਂ ਦੀ ਵਿਆਖਿਆ ਕਰਦਾ ਹੈ ਅਤੇ ਹੋਰ ਪ੍ਰਾਪਤੀਆਂ ਦੇ ਅਸਰ ਨੂੰ ਨਜ਼ਰ-ਅੰਦਾਜ਼ ਕਰ ਦਿੰਦਾ ਹੈ, ਜਾਂ ਉਨ੍ਹਾਂ ਨਤੀਜਿਆਂ ਪ੍ਰਤੀ ਸਾਧਾਰਨ ਜਿਹੇ ਅੰਕ ਲਾ ਦਿੰਦਾ ਹੈ। ਇਹ ਧਾਰਨਾ ਗ਼ਲਤ ਜਿਹੀ ਲੱਗਦੀ ਹੈ। ਜੇ ਧਰਤੀ ਦੀ ਹਰ ਇਕ ਵਸਤੂ ਕਿਸੇ ਦੂਜੀ ਵਸਤੂ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ, ਤਾਂ ਅਸੂਲੀ ਤੌਰ ਤੇ ਤਾਂ ਇਸ ਸਮੱਸਿਆ ਦੇ ਵੱਖਰੇ-ਵੱਖਰੇ ਭਾਗਾਂ ਨੂੰ ਅੱਡ ਕਰਕੇ ਖੋਜਣ ਨਾਲ ਕੋਈ ਹੱਲ ਨਹੀਂ ਨਿਕਲ ਸਕਦਾ। ਤਾਂ ਵੀ ਇਹੋ ਇਕ ਢੰਗ ਹੈ, ਜਿਸ ਦੁਆਰਾ ਅਸੀਂ ਭੂਤਕਾਲ ਵਿੱਚ, ਕੁਝ ਨਾ ਕੁਝ ਪ੍ਰਾਪਤੀ ਕੀਤੀ ਹੈ।

ਇਹ ਇਕ ਮੰਨੀ ਜਾ ਚੁੱਕੀ ਉਦਾਹਰਣ ਨਿਊਟਨ ਦਾ ਚੁੰਬਕ ਸ਼ਕਤੀ ਵਾਲਾ ਗੁਰ ਹੈ, ਦੋ ਗ੍ਰਹਿ ਵਿਚਲੀ ਖਿੱਚ ਉਨ੍ਹਾਂ ਦੋਹਾਂ ਗ੍ਰਹਿ ਨਾਲ ਹੀ ਸੰਬੰਧਿਤ ਹੈ, ਭਾਵ ਉਸ ਦੀ ਬਣਤਰ ਅਤੇ ਆਕਾਰ ਨੂੰ ਹੀ ਮੁੱਖ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ। ਬਾਕੀ ਉਹ ਗ੍ਰਹਿ ਕਿਸ ਪਦਾਰਥ ਦੇ ਬਣੇ ਹੋਏ ਹਨ, ਦਾ ਉਨ੍ਹਾਂ ਉੱਤੇ ਕੋਈ ਅਸਰ ਨਹੀਂ ਪੈਂਦਾ। ਇਸ ਲਈ ਇਹ ਜਾਣਨ ਦੀ ਲੋੜ ਹੀ ਨਹੀਂ ਹੈ, ਕਿ ਸੂਰਜ ਅਤੇ ਹੋਰ ਗ੍ਰਹਿ ਕਿਸ ਚੀਜ਼ ਦੇ ਬਣੇ ਹੋਏ ਹਨ, ਤਾਂ ਜੋ ਉਨ੍ਹਾਂ ਦੀ ਘੁੰਮਣ-ਘੇਰੀ ਦਾ ਪਤਾ ਲੱਗ ਸਕੇ।

ਅੱਜ ਕੱਲ੍ਹ, ਵਿਗਿਆਨਿਕ ਧਰਤੀ ਦੀ ਵਿਆਖਿਆ ਦੋ ਮੁੱਢਲੇ ਸਿਧਾਂਤਾਂ-ਮਾਤ੍ਰਕ ਸਿਧਾਂਤ ਅਤੇ ਗਣਿਤ ਗੁਰ ਦੇ ਆਧਾਰ ਤੇ ਕਰਦੇ ਹਨ। ਚਾਲੂ ਸ਼ਤਾਬਦੀ ਦੀਆਂ ਇਹ ਸੁਚਾਰੀਆਂ ਅਤੇ ਮਹਾਨ ਪ੍ਰਾਪਤੀਆਂ ਹਨ। ਮਾਕ ਸਿਧਾਂਤ ਧਰਤੀ ਦੀ ਚੁੰਬਕ ਸ਼ਕਤੀ ਅਤੇ ਇਸ ਦੀ ਬਣਤਰ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ। ਅਰਥਾਤ ਕੁਝ ਮੀਲਾਂ ਤੋਂ ਸ਼ੁਰੂ ਕਰਕੇ ਅਰਬਾਂ ਖ਼ਰਬਾਂ ਮੀਲਾਂ (1 ਦੇ ਨਾਲ 24 ਸਿਫ਼ਰ ਲਾ ਕੇ) ਦੇ ਪੈਮਾਨੇ ਅਨੁਸਾਰ, ਪ੍ਰਤੱਖ ਤੌਰ ‘ਤੇ ਨਜ਼ਰ ਆ ਰਹੀ ਧਰਤੀ ਦੀ ਵਿਆਖਿਆ ਕਰਦਾ ਹੈ। ਗਣਿਤ ਗੁਰ, ਦੂਜੇ ਬੰਨੇ, ਇਹ ਵਿਆਖਿਆ ਨਿੱਕੇ ਤੋਂ ਨਿੱਕੇ ਪੈਮਾਨੇ ਅਨੁਸਾਰ (ਇਕ ਇੰਚ ਦੇ ਕਰੋੜਵੇਂ ਹਿੱਸੇ ਅਨੁਸਾਰ)। ਮੰਦ-ਭਾਗੀ ਗੱਲ ਤਾਂ ਇਹ ਹੈ ਕਿ ਇਹ ਦੋਵੇਂ ਸਿਧਾਂਤ ਇਕ ਦੂਜੇ ਨਾਲ ਮੇਲ ਨਹੀਂ ਖਾਂਦੇ ਅਤੇ ਇਹ ਦੋਵੇਂ ਸਹੀ ਵੀ ਨਹੀਂ ਮੰਨੇ ਜਾ ਸਕਦੇ। ਅਜੋਕੇ ਸਰੀਰਕ ਵਿਗਿਆਨ ਦੇ ਪਿੜ .ਦੀ ਅਤੇ ਇਸ ਪੁਸਤਕ ਦੀ ਵਿਸ਼ਾ-ਪੂਰਤੀ ਦੀ ਇਹ ਕੋਸ਼ਿਸ਼ ਹੈ ਕਿ ਕੋਈ ਅਜਿਹਾ ਨਵਾਂ ਸਿਧਾਂਤ ਖੋਜਿਆ ਜਾਵੇ, ਜਿਹੜਾ ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਸਿਧਾਂਤਾਂ ਨੂੰ ਜੋੜ ਦੇਵੇ-ਚੁੰਬਕ ਸ਼ਕਤੀ ਦਾ ਗਣਿਤ-ਰੂਪੀ ਸਿਧਾਂਤ। ਸਾਡੇ ਕੋਲ ਹਾਲੇ ਤੱਕ ਅਜਿਹਾ ਸਿਧਾਂਤ ਮੌਜੂਦ ਨਹੀਂ ਹੈ ਅਤੇ ਸ਼ਾਇਦ ਸਾਨੂੰ ਹਾਲੇ ਹੋਰ ਕਿਤਨਾ ਹੀ ਚਿਰ ਪ੍ਰਾਪਤ ਵੀ ਨਾ ਹੋ ਸਕੇ, ਪਰੰਤੂ ਅਸੀਂ ਉਨ੍ਹਾਂ, ਗੁਰਾਂ ਤੋਂ ਜਾਣੂ ਹੋ ਚੁੱਕੇ ਹਾਂ, ਜੋ ਉਸ ਸਿਧਾਂਤ ਵਿੱਚ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ। ਆਉਣ ਵਾਲੇ ਅੰਕਾਂ ਵਿੱਚ ਅਸੀਂ ਦੇਖਾਂਗੇ ਕਿ ਸਾਨੂੰ ਉਨ੍ਹਾਂ ਪ੍ਰਾਪਤੀਆਂ ਦਾ ਖਾਸਾ ਗਿਆਨ ਹੈ, ਜੋ ਚੁੰਬਕ ਸ਼ਕਤੀ ਦੀ ਗਣਿਤ-ਕਿਰਿਆ ਤੋਂ ਪ੍ਰਗਟ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ।

ਜੇ ਤੁਸੀਂ ਵਿਸ਼ਵਾਸ ਕਰਦੇ ਹੋਈਏ ਕਿ ਧਰਤੀ ਆਪ-ਮੁਹਾਰੀ ਜਾਂ ਆਪਹੁਦਰੀ ਨਹੀਂ ਹੈ, ਸਗੋਂ ਇਹ ਪੱਕੇ ਨਿਯਮਾਂ ਦੇ ਅਧੀਨ ਕਿਰਿਆਸ਼ੀਲ ਹੈ, ਤਾਂ ਤੁਹਾਨੂੰ ਵੱਖਰੇ ਅੰਸ਼ਕ ਸਿਧਾਂਤਾਂ ਨੂੰ ਇਕੋ ਸਿਧਾਂਤ ਵਿੱਚ ਜੋੜਨਾ ਪਵੇਗਾ, ਜਿਹੜਾ ਧਰਤੀ ਦੇ ਸਾਰੇ ਪੱਖਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰਦਾ ਹੋਵੇ। ਪਰੰਤੂ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਸਿਧਾਂਤ ਦੀ ਖੋਜ ਵਿੱਚ ਇਕ ਦਵੰਦ ਮੌਜੂਦ ਹੈ। ਉਪਰੋਕਤ ਵਿਗਿਆਨਿਕ ਸਿਧਾਂਤਾਂ ਤੋਂ ਉਪਜੇ ਵਿਚਾਰਾਂ ਤੋਂ ਐਉਂ ਜਾਪਦਾ ਹੈ ਕਿ ਅਸੀਂ ਤਰਕ ਦੇ ਧਾਰਨੀ ਹਾਂ ਅਤੇ ਅਸੀਂ ਧਰਤੀ ਬਾਰੇ ਜਿਵੇਂ ਚਾਹੀਏ ਉਵੇਂ ਸੋਚ ਲਈਏ ਅਤੇ ਜੋ ਕੁਝ ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ, ਉਸ ਨੂੰ ਮੁੱਖ ਰੱਖ ਕੇ ਮਨਮਰਜ਼ੀ ਦੇ ਨਤੀਜੇ ਕੱਢ ਲਈਏ। ਅਜਿਹੀ ਸਥਿਤੀ ਵਿੱਚ, ਇਹ ਫ਼ਰਜ਼ ਕਰ ਲੈਣਾ ਗ਼ਲਤ ਨਹੀਂ ਹੋ ਸਕਦਾ, ਕਿ ਅਸੀਂ ਉਨ੍ਹਾਂ, ਨਿਯਮਾਂ ਨੂੰ ਲੱਭਣ ਵਿੱਚ ਲਗਭਗ ਸਫ਼ਲ ਹੋ ਸਕਦੇ ਹਾਂ। ਜਿਨ੍ਹਾਂ ਨਿਯਮਾਂ’ ਦੇ ਅਧੀਨ ਸਾਡੀ ਧਰਤੀ ਚੱਲ ਰਹੀ ਹੈ। ਫੇਰ ਵੀ ਜੇ ਕੋਈ ਸਾਂਝਾ ਪੂਰਨ ਸਿਧਾਂਤ ਪ੍ਰਾਪਤ ਹੋ ਜਾਵੇ, ਤਾਂ ਸਾਡੇ ਉਪਰਾਲਿਆਂ ਦਾ ਨਿਰਣਾ ਵੀ ਹੋ ਸਕੇਗਾ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਅਜਿਹੇ ਸਿਧਾਂਤ ਨਾਲ ਸਾਡੀ ਇਸ ਖੋਜ ਦੇ ਨਤੀਜਿਆਂ ਦਾ ਨਿਰਣਾ ਵੀ ਹੋ ਜਾਵੇਗਾ। ਪਰੰਤੂ ਇਹ ਨਿਰਣਾ ਕਿਉਂ ਹੋਵੇ ਕਿ ਅਸੀਂ ਪ੍ਰਾਪਤ ਗਵਾਹੀਆਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਸਹੀ ਨਤੀਜੇ ਕੱਢੇ ਹਨ। ਕੀ ਇਸ ਨਾਲ ਇਹ ਵੀ ਸਿੱਧ ਨਹੀਂ ਹੋ ਸਕਦਾ ਕਿ ਸਾਡੇ ਨਤੀਜੇ ਗ਼ਲਤ ਹਨ ਜਾਂ ਕੋਈ ਵੀ ਨਤੀਜਾ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੋਇਆ।

ਮੈਂ ਤਾਂ ਇਸ ਦਾ ਉੱਤਰ ਕੇਵਲ ਡਾਰਵਿਨ (Darwin) ਦੇ ਕੁਦਰਤੀ ਚੋਣ ਦੇ ਸਿਧਾਂਤ ਦੇ ਆਧਾਰ ਉੱਤੇ ਦੇ ਸਕਦਾ ਹਾਂ। ਵਿਚਾਰ ਤਾਂ ਇਹ ਹੈ ਕਿ ਆਬਾਦੀ ਵਿੱਚ ਆਪਣੇ ਆਪ ਵਾਧਾ ਕਰਨ ਵਾਲੀਆਂ ਜੱਥੇਬੰਦੀਆਂ ਵਿੱਚ, ਜੀਵ-ਵਿਗਿਆਨਿਕ ਪਦਾਰਥਾਂ ਵਿੱਚ ਅੰਤਰ ਹੋਇਆ ਕਰਦਾ ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਦੇ ਢੰਗ ਵੀ ਵੱਖਰੇ- ਵੱਖਰੇ ਹੁੰਦੇ ਹਨ, ਜੋ ਵਿਅਕਤੀਗਤ ਤੌਰ ‘ਤੇ ਮੌਜੂਦ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ। ਅਜਿਹੇ ਫ਼ਰਕਾਂ ਦਾ ਅਰਥ ਹੈ ਕਿ ਕੁਝ ਵਿਅਕਤੀ, ਆਪਣੇ ਆਲੇ-ਦੁਆਲੇ ਫੈਲੀ ਹੋਈ ਦੁਨੀਆਂ ਬਾਰੇ ਸਹੀ ਨਤੀਜੇ ਕੱਢਣ ਵਿੱਚ ਦੂਜਿਆਂ ਨਾਲੋਂ ਵਧੇਰੇ ਸਿਆਣੇ ਹਨ ਅਤੇ ਉਸੇ ਹਿਸਾਬ ਨਾਲ ਉਹ ਕੰਮ ਕਰਦੇ ਹਨ। ਅਜਿਹੇ ਵਿਅਕਤੀ ਕਾਇਮ ਰਹਿ ਸਕਣਗੇ ਅਤੇ ਆਬਾਦੀ ਵਿੱਚ ਵਾਧਾ ਕਰਦੇ ਰਹਿਣਗੇ ਅਤੇ ਉਨ੍ਹਾਂ ਦਾ ਰਵੱਈਆ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਵਿਚਾਰ ਭਾਰੂ ਹੋ ਜਾਣਗੇ। ਬੀਤੇ ਸਮੇਂ ਵਿੱਚ ਇਹ ਸੱਚ ਸਿੱਧ ਹੋ ਚੁੱਕਾ ਹੈ ਕਿ ਸਿਆਣੇ ਅਤੇ ਵਿਗਿਆਨਿਕ ਖੋਜ ਕਰਨ ਵਾਲਿਆਂ ਨੂੰ ਕਾਇਮ ਰਹਿਣ ਵਿੱਚ ਲਾਭ ਪੁੱਜਦਾ ਰਿਹਾ ਹੈ। ਹਾਲੇ ਵੀ ਇਹ. ਗੱਲ ਸਪੱਸ਼ਟ ਨਹੀਂ ਹੋ ਸਕੀ, ਕਿ ਬੱਸ ਇੰਨੀ ਗੱਲ ਹੈ। ਸਾਡੀਆਂ ਵਿਗਿਆਨਿਕ ਖੋਜਾਂ ਸਾਨੂੰ ਮਲੀਆਮੇਟ ਵੀ ਕਰ ਸਕਦੀਆਂ ਹਨ, ਅਤੇ ਜੇ ਉਹ ਸਾਨੂੰ ਤਬਾਹ ਨਹੀਂ ਵੀ ਕਰਦੀਆਂ ਤਾਂ ਪੂਰਨ ਸਿਧਾਂਤ ਨਾਲ ਸਾਡੀ ਕਾਇਮੀ ਦੇ ਮਾਮਲੇ ਵਿੱਚ ਬਹੁਤਾ ਫ਼ਰਕ ਨਹੀਂ ਪੈ ਸਕਦਾ, ਪਰੰਤੂ ਜੇ ਧਰਤੀ ਦਾ ਵਿਕਾਸ ਕਿਸੇ ਬੰਧੇਜ ਨਾਲ ਹੁੰਦਾ ਜਾ ਰਿਹਾ ਹੈ, ਤਾਂ ਸਾਨੂੰ ਉਮੀਦ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਕਿ ਕੁਦਰਤੀ ਚੋਣ ਸਦਕਾ ਪ੍ਰਾਪਤ ਹੋਈਆਂ ਤਰਕਸ਼ੀਲ ਯੋਗਤਾਵਾਂ, ਇਕ ਸਾਂਝੇ ਪੂਰਨ ਸਿਧਾਂਤ ਦੀ ਖੋਜ ਵਿੱਚ ਸਾਡੀ ਸਹਾਇਤਾ ਕਰ ਸਕਣਗੀਆਂ ਅਤੇ ਅਸੀਂ ਗ਼ਲਤ ਨਤੀਜੇ ਕੱਢਣ ਤੋਂ ਬਚ ਜਾਵਾਂਗੇ।

ਕਿਉਂਕਿ ਸਾਡੇ ਹੁਣ ਤੱਕ ਦੇ ਅੰਸ਼ਕ ਸਿਧਾਂਤ, ਕੁਝ ਗੰਭੀਰ ਹਾਲਤਾਂ ਨੂੰ ਛੱਡ ਕੇ, ਸਹੀ-ਸਹੀ ਨਤੀਜੇ ਕੱਢਣ ਲਈ ਕਾਫ਼ੀ ਹਨ; ਧਰਤੀ ਬਾਰੇ ਅੰਤਮ ਸਿਧਾਂਤ ਘੜਨਾ ਮੁਸ਼ਕਲ ਜਾਪਦਾ ਹੈ, ਜਿਸ ਦੇ ਕਾਰਨ ਅਸਲੀ ਕਠਿਨਾਈਆਂ ਹਨ। (ਭਾਵੇਂ ਇਹ ਅਨੁਭਵ ਕਰਨਾ ਜਾਇਜ਼ ਹੈ ਕਿ ਇਸੇ ਪ੍ਰਕਾਰ ਦੀਆਂ ਦਲੀਲਾਂ ਮਾਤ੍ਰਕ ਵਿਗਿਆਨ ਅਤੇ ਗਣਿਤ ਕਿਰਿਆ ਦੇ ਵਿਰੁੱਧ ਵੀ ਦਿੱਤੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ਅਤੇ ਇਨ੍ਹਾਂ ਸਿਧਾਂਤਾਂ ਸਦਕਾ ਅਸੀਂ ਊਰਜਾ ਅਤੇ ਊਰਜੀ ਜੰਤਰਾਂ ਦੇ ਪਿੜ ਵਿੱਚ ਪਰਿਵਰਤਨ ਲਿਆ ਸਕੇ ਹਾਂ।) ਇਸ ਲਈ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਪੂਰਨ ਅਤੇ ਸਾਂਝੇ ਸਿਧਾਂਤ ਦੀ ਖੋਜ ਆਪਣੀ ਨਸਲ ਜਾਰੀ ਰੱਖਣ ਲਈ ਸਾਡੀ ਸਹਾਇਤਾ ਨਾ ਕਰ ਸਕੇ। ਸ਼ਾਇਦ ਇਹ ਸਾਡੇ ਜੀਵਨ ਢੰਗ ਨੂੰ ਵੀ ਪ੍ਰਭਾਵਿਤ ਨਾ ਕਰ ਸਕੇ। ਪਰੰਤੂ ਉਹ ਸਭਿਅਤਾ ਦੇ ਅਰੰਭ ਤੋਂ ਲੈ ਕੇ ਹੁਣ ਤੱਕ, ਘਟਨਾਵਾਂ ਨੂੰ ਅਜੋੜ ਅਤੇ ਗੁੰਝਲਦਾਰ ਦੇਖ ਕੇ ਸੰਤੁਸ਼ਟ ਨਹੀਂ ਹੋਏ। ਉਹ ਧਰਤੀ ਦੇ ਗੁੱਝੇ ਅਮਲਾਂ ਨੂੰ ਸਮਝਣ ਲਈ ਤਰਸਦੇ ਰਹੇ ਹਨ। ਅਸੀਂ ਅੱਜ ਵੀ ਇਹ ਜਾਣਨ ਦੇ ਚਾਹਵਾਨ ਹਾਂ ਕਿ ਅਸੀਂ ਇੱਥੇ ਕਿਉਂ ਵਿਚਰ ਰਹੇ ਹਾਂ ਅਤੇ ਅਸੀਂ ਕਿੱਥੋਂ ਆਏ ਹਾਂ। ਮਨੁੱਖਤਾ ਦੀ ਗਿਆਨ ਪ੍ਰਾਪਤੀ ਦੀ ਡੂੰਘੀ ਇੱਛਾ-ਸ਼ਕਤੀ ਹੀ ਸਾਨੂੰ ਖੋਜ ਵਿੱਚ ਜੁਟੇ ਰਹਿਣ ਲਈ ਬਹੁਤ ਹੱਦੇ ਤੱਕ ਜ਼ਿੰਮੇਵਾਰ ਹੈ ਅਤੇ ਸਾਡਾ ਜੀਵਨ ਮਨੋਰਥ ਇਸ ਧਰਤੀ ਦੀ ਪੂਰਨ ਵਿਆਖਿਆ ਕਰਨ ਦੇ ਯੋਗ ਹੋਣ ਤੋਂ ਘੱਟ ਨਹੀਂ ਹੈ।

ਪੁਲਾੜ ਅਤੇ ਸਮਾਂ

ਗ੍ਰਹਿ ਦੀ ਹਰਕਤ ਬਾਰੇ ਸਾਡੇ ਵਿਚਾਰ ਗਲੀਲੀਓ ਅਤੇ ਨਿਊਟਨ ਦੇ ਸਮੇਂ ਤੋਂ ਸ਼ੁਰੂ ਹੁੰਦੇ ਹਨ। ਉਸ ਤੋਂ ਪਹਿਲਾਂ ਲੋਕ ਅਰਸਤੂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ, ਜਿਸ ਦਾ ਕਥਨ ਸੀ ਕਿ ਇਕ ਗ੍ਰਹਿ ਟਿਕਾਓ ਦੀ ਕੁਦਰਤੀ ਅਵਸਥਾ ਵਿੱਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਅਜਿਹਾ ਗ੍ਰਹਿ ਕੇਵਲ ਉਦੋਂ ਹੀ ਹਿਲਦਾ ਹੈ, ਜਦੋਂ ਕੋਈ ਬਾਹਰੀ ਸ਼ਕਤੀ ਉਸ ਨੂੰ ਧੱਕਾ ਮਾਰੇ। ਇਸ ਦਾ ਭਾਵ ਇਹ ਹੋਇਆ ਕਿ ਭਾਰੀ ਚੀਜ਼ ਹੌਲੀ ਚੀਜ਼ ਨਾਲੋਂ ਵਧੇਰੇ ਤੇਜ਼ੀ ਨਾਲ ਡਿਗਦੀ ਹੈ; ਕਿਉਂਕਿ ਇਸ ਨੂੰ ਧਰਤੀ ਦੀ ਖਿੱਚ ਅਧਿਕਤਰ ਹੁੰਦੀ ਹੈ।

ਅਰਸਤੂ ਦੇ ਮੱਤ ਅਨੁਸਾਰ, ਸਿਰਫ਼ ਸੋਚਣ ਨਾਲ ਹੀ ਕੋਈ ਬੰਦਾ, ਧਰਤੀ ਨੂੰ ਚਲਾਉਣ ਵਾਲੇ ਨਿਯਮ ਘੜ ਸਕਦਾ ਹੈ, ਅਜਿਹੇ ਅਮਲ ਲਈ ਪ੍ਰਤੱਖ ਨਜ਼ਾਰਿਆਂ ਦੀ ਪੜਤਾਲ ਕਰਨ ਦੀ ਕੋਈ ਲੋੜ ਨਹੀਂ ਹੈ। ਇਸ ਲਈ ਗਲੀਲੀਓ ਦੇ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਕਿਸੇ ਨੇ ਇਹ ਪਰਖ ਕਰਨ ਦੀ ਖੇਚਲ ਨਹੀਂ ਸੀ ਕੀਤੀ ਕਿ ਕੀ ਸੱਚਮੁੱਚ ਵੱਖਰੇ ਭਾਰ ਵਾਲੀਆਂ ਵਸਤਾਂ ਵੱਖਰੇ ਸਮੇਂ ਵਿੱਚ ਹੇਠਾਂ ਡਿੱਗਦੀਆਂ ਹਨ ਅਤੇ ਡਿਗਣ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਵੀ ਅੰਤਰ ਹੁੰਦਾ ਹੈ। ਕਹਿੰਦੇ ਹਨ ਕਿ ਗਲੀਲੀਓ ਨੇ ਅਰਸਤੂ ਦੇ ਮੱਤ ਨੂੰ ਗ਼ਲਤ ਸਾਬਤ ਕਰਨ ਲਈ ਪੀਸਾ ਬੁਰਜ (Tower of PISA) ਤੋਂ ਭਾਰੀਆਂ ਚੀਜ਼ਾਂ ਸੁੱਟ ਕੇ ਦਿਖਾਇਆ। ਇਹ ਕਹਾਣੀ ਤਾਂ ਸਰਾਸਰ ਝੂਠੀ ਹੈ, ਪਰ ਗਲੀਲੀਓ ਨੇ ਅਜਿਹਾ ਇਕ ਤਜਰਬਾ ਜ਼ਰੂਰ ਕੀਤਾ, ਉਸ ਨੇ ਇਕ ਪੱਧਰੀ ਢਲਾਣ ਤੋਂ ਵੱਖਰੇ-ਵੱਖਰੇ ਭਾਰ ਵਾਲੀਆਂ ਗੇਂਦਾਂ ਹੇਠਾਂ ਜ਼ਰੂਰ ਰੋਹੜੀਆਂ ਸਨ। ਗੱਲ ਤਾਂ ਭਾਰੀ ਚੀਜ਼ਾਂ ਦੇ ਸਿੱਧੀਆਂ ਸਤੋਲ ਹੇਠਾਂ ਡਿੱਗਣ ਵਾਲੀ ਹੀ ਹੈ, ਪਰ ਇਨ੍ਹਾਂ ਦੀ ਰਫ਼ਤਾਰ ਮਠੇਰੀ ਹੋਣ ਕਰਕੇ ਉਨ੍ਹਾਂ ਦੀ ਜਾਂਚ ਕਰਨੀ ਸੌਖੀ ਹੈ। ਗਲੀਲੀਓ ਦੇ ਨਾਪ ਅਨੁਸਾਰ ਹਰ ਇਕ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਇਕੋ ਜਿਹੀ ਤੇਜ਼ੀ ਆਉਂਦੀ ਹੈ, ਸੁੱਟੀਆਂ ਭਾਵੇਂ ਕਿਤਨੀ ਵੀ ਉੱਚਾਈ ਤੋਂ ਜਾਣ। ਉਦਾਹਰਣ ਵਜੋਂ, ਜੇ ਤੁਸੀਂ ਇਕ ਗੇਂਦ ਨੂੰ ਇਕ ਢਲਾਣ ਉੱਤੇ ਸੁੱਟੋ, ਤਾਂ ਜੇ ਉਹ ਤੁਹਾਡੇ ਦਸ ਮੀਟਰ ਦੇ ਟਾਕਰੇ ਵਿੱਚ ਇਕ ਮੀਟਰ ਚੱਲੇਗੀ, ਗੇਂਦ ਦੀ ਰਫ਼ਤਾਰ, ਇਕ ਸਕਿੰਟ ਮਗਰੋਂ ਇਕ ਮੀਟਰ ਪ੍ਰਤੀ ਸਕਿੰਟ, ਦੋ ਮੀਟਰ ਪ੍ਰਤੀ ਸਕਿੰਟ, ਦੋ ਸਕਿੰਟਾਂ ਮਗਰੋਂ, ਅਤੇ ਇਸੇ ਤਰ੍ਹਾਂ ਰਫ਼ਤਾਰ ਵੱਧਦੀ ਜਾਵੇਗੀ। ਗੇਂਦ ਦਾ ਭਾਰ ਭਾਵੇਂ ਕਿਤਨਾ ਵੀ ਹੋਵੇ। ਹਾਂ ਇਹ ਸਹੀ ਹੈ ਕਿ ਸਿੱਕਾ ਪੰਖ ਨਾਲੋਂ ਤੇਜ਼ੀ ਨਾਲ ਡਿਗੇਗਾ, ਪਰੰਤੂ ਪੰਖ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਵਾਯੂ ਰੁਕਾਵਟ ਬਣ ਜਾਂਦੀ ਹੈ। ਜੇ ਕੋਈ ਅਜਿਹੀਆਂ ਦੋ ਚੀਜ਼ਾਂ ਸੁੱਟ ਦੇਵੇ, ਜਿਨ੍ਹਾਂ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਵਾਯੂ ਰੁਕਾਵਟ ਨਾ ਬਣਦੀ ਹੋਵੇ, ਜਿਵੇਂ ਕਿ ਸਿੱਕੇ ਵਰਗੀਆਂ ਵਸਤਾਂ, ਤਾਂ ਉਹ ਇੱਕੋ ਜਿਹੀ ਰਫ਼ਤਾਰ ਨਾਲ ਡਿਗਣਗੀਆਂ।

ਗਲੀਲੀਓ ਦੇ ਪੈਮਾਨਿਆਂ ਨੂੰ ਨਿਊਟਨ ਨੇ ਰਫ਼ਤਾਰ ਦੇ ਨਿਯਮਾਂ ਦਾ ਆਧਾਰ ਬਣਾਇਆ ਸੀ। ਗਲੀਲੀਓ ਦੇ ਤਜਰਬਿਆਂ ਅਨੁਸਾਰ, ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਢਲਾਣ ਦੇ ਨਾਲ-ਨਾਲ ਰੋਹੜੀ ਜਾਂਦੀ ਸੀ, ਤਾਂ ਉਸ ਵਸਤੂ ਦਾ ਭਾਰ ਹੀ ਉਸ ਦੀ ਰਫ਼ਤਾਰ ਦਾ ਆਧਾਰ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ਅਤੇ ਉਹ ਰਫ਼ਤਾਰ ਲਗਾਤਾਰ ਵੱਧਦੀ ਰਹਿੰਦੀ ਸੀ। ਉਸ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਸੀ ਕਿ ਕਿਸੇ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਫ਼ਰਕ ਪਾਉਣ ਲਈ ਵਸਤੂ ਦਾ ਭਾਰ ਮੁਖ ਆਧਾਰ ਹੁੰਦਾ ਸੀ। ਨਾ ਕੇਵਲ ਉਸ ਨੂੰ ਰੋਹੜਨ ਲਈ ਹੀ, ਜਿਹਾ ਕਿ ਪਹਿਲਾਂ ਸੋਚਿਆ ਜਾਂਦਾ ਸੀ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਵੀ ਹੈ ਕਿ ਜੇ ਕਿਸੇ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਫ਼ਰਕ ਪਾਉਣ ਵਾਲੀ ਕੋਈ ਸ਼ਕਤੀ ਮੌਜੂਦ ਨਾ ਹੋਵੇ, ਤਾਂ ਉਹ ਵਸਤੂ ਇਕੋ ਸੇਧ ਵਿੱਚ, ਇੱਕੋ ਰਫ਼ਤਾਰ ਨਾਲ ਚਲਦੀ ਰਹੇਗੀ। ਇਹ ਵਿਚਾਰ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਨਿਊਟਨ ਨੇ ਆਪਣੀ ਪੁਸਤਕ ‘Principia Mathematicia’ ਵਿੱਚ ਪ੍ਰਗਟ ਕੀਤਾ ਸੀ। ਜੋ 1687 ਈਸਵੀਂ ਵਿੱਚ ਪ੍ਰਕਾਸ਼ਤ ਹੋਈ ਸੀ ਅਤੇ ਜਿਸ ਨੂੰ ਨਿਊਟਨ ਦਾ ਪ੍ਰਥਮ ਨਿਯਮ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ। ਨਿਊਟਨ ਦੇ ਦੂਜੇ ਨਿਯਮ ਵਿੱਚ ਦੱਸਿਆ ਗਿਆ ਹੈ ਕਿ ਜੇ ਕਿਸੇ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਉੱਤੇ ਅਸਰ ਪਾਉਣ ਵਾਲੀ ਕੋਈ ਵੀ ਸ਼ਕਤੀ ਨਾ ਹੋਵੇ, ਤਾਂ ਕੀ ਨਤੀਜਾ ਨਿਕਲਦਾ ਹੈ ? ਇਸ ਨਿਯਮ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਉਸ ਸ਼ਕਤੀ ਦੀ ਮਾਤਰਾ ਅਨੁਸਾਰ ਵਾਧਾ ਹੋਵੇਗਾ ਜਾਂ ਉਸ ਰਫ਼ਤਾਰ ਵਿੱਚ ਫ਼ਰਕ ਪੈ ਜਾਵੇਗਾ। (ਉਦਾਹਰਣ ਵਜੋਂ, ਜੇ ਸ਼ਕਤੀ ਦੀ ਮਾਤਰਾ ਦੁੱਗਣੀ ਹੋਵੇਗੀ ਤਾਂ ਰਫ਼ਤਾਰ ਵਿੱਚ ਵੀ ਦੁੱਗਣਾ ਵਾਧਾ ਹੋ ਜਾਵੇਗਾ।) ਵਸਤੂ ਦਾ ਆਕਾਰ ਵਡੇਰਾ ਹੋਣ ਦੀ ਸੂਰਤ ਵਿੱਚ ਵੀ, ਜਾਂ ਵਸਤੂਆਂ ਦੀ ਗਿਣਤੀ ਵੱਧ ਹੋਵੇ ਤਾਂ ਵੀ ਰਫ਼ਤਾਰ ਮਠੇਰੀ ਹੋਵੇਗੀ। ਦੁੱਗਣੇ ਆਕਾਰ ਵਾਲੀ ਵਸਤੂ ਉੱਤੇ ਇਕੋ ਜਿਹੀ ਸ਼ਕਤੀ ਨਾਲ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਅੱਧੀ ਰਹਿ ਜਾਵੇਗੀ। ਇਕ ਜਾਣੀ-ਪਛਾਣੀ ਮਿਸਾਲ, ਇਕ ਕਾਰ ਤੋਂ ਮਿਲਦੀ ਹੈ, ਅਧਿਕਤਰ ਸ਼ਕਤੀ ਵਾਲੇ ਇੰਜਣ ਨਾਲ ਰਫ਼ਤਾਰ ਵੀ ਤੇਜ਼ਤਰ ਹੋਵੇਗੀ ਪਰੰਤੂ ਜੇ ਉਸੇ ਇੰਜਣ ਨੂੰ ਵਧੇਰੇ ਭਾਰੀ ਕਾਰ ਚਲਾਉਣੀ ਪਵੇ, ਤਾਂ ਕਾਰ ਦੀ ਰਫ਼ਤਾਰ ਘੱਟ ਜਾਵੇਗੀ। ਰਫ਼ਤਾਰ ਦੇ ਨਿਯਮਾਂ ਤੋਂ ਇਲਾਵਾ, ਨਿਊਟਨ ਨੇ ਚੁੰਬਕ ਖਿੱਚ ਦੀ ਸ਼ਕਤੀ ਦਾ ਨਿਯਮ ਵੀ ਲੱਭ ਲਿਆ ਸੀ। ਉਸ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਹਰ ਇਕ ਵਸਤੂ ਦੂਜੀ ਵਸਤੂ ਨੂੰ ਆਪਣੇ ਵੱਲ ਉਤਨੀ ਖਿੱਚ ਪਾਉਂਦੀ ਹੈ, ਜਿੰਨਾ ਅਨੁਪਾਤ ਉਨ੍ਹਾਂ ਦੇ ਆਕਾਰਾਂ ਵਿੱਚ ਹੁੰਦਾ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਦੋ ਵਸਤੂਆਂ ਵਿਚਕਾਰ ਖਿੱਚ-ਸ਼ਕਤੀ ਦੁੱਗਣੀ ਹੋ ਜਾਂਦੀ ਹੈ, ਜੇ ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇਕ ਵਸਤੂ (ਭਾਵ ਵਸਤੂ ਓ) ਦਾ ਆਕਾਰ ਦੁਗਣਾ ਹੋਵੇ। ਅਜਿਹੀ ਅਵਸਥਾ ਦੀ ਤੁਸੀਂ ਸਹਿਜੇ ਹੀ ਉਮੀਦ ਵੀ ਕਰ ਸਕਦੇ ਹੋ ਕਿਉਂਕਿ ਦੇਖਣ ਵਾਲੇ ਨੂੰ ਨਵੀਂ ਵਸਤੂ “ਓ” ਮੁੱਢਲੇ ਆਕਾਰ ਵਾਲੀਆਂ ਦੋ ਵਸਤੂਆਂ ਦੇ ਆਕਾਰ ਦੀ ਬਣੀ ਹੋਈ ਨਜ਼ਰ ਆਵੇਗੀ। ਹਰ ਇਕ ਵਸਤੂ, ਵਸਤੂ “ਅ” ਨੂੰ ਆਪਣੀ-ਆਪਣੀ ਸ਼ਕਤੀ ਦੇ ਆਧਾਰ ‘ਤੇ ਖਿੱਚ ਪਾਵੇਗੀ। ਇਸ ਤਰ੍ਹਾਂ “ਓ” ਅਤੇ “ਅ” ਵਸਤੂਆਂ ਵਿਚਕਾਰ ਪਹਿਲੀ ਸ਼ਕਤੀ ਨਾਲੋਂ ਕੁੱਲ ਸ਼ਕਤੀ ਦੁੱਗਣੀ ਹੋ ਜਾਵੇਗੀ। ਜੇ ਮੰਨ ਲਓ ਕਿ ਇਕ ਵਸਤੂ ਦਾ ਆਕਾਰ ਦੁੱਗਣਾ ਹੋਵੇ ਅਤੇ ਦੂਜੀ ਵਸਤੂ ਦਾ ਆਕਾਰ ਤਿਗਣਾ ਹੋਵੇ, ਤਾਂ ਖਿੱਚ ਸ਼ਕਤੀ ਛੇ ਗੁਣਾ ਵੱਧ ਜਾਵੇਗੀ। ਹੁਣ ਤੁਸੀਂ ਦੇਖ ਸਕਦੇ ਹੋ ਕਿ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਇਕੋ ਰਫ਼ਤਾਰ ਨਾਲ ਕਿਉਂ ਡਿੱਗਦੀਆਂ ਹਨ। ਦੁੱਗਣ ਭਾਰ ਵਾਲੀ ਵਸਤੂ ਦੁੱਗਣੀ ਖਿੱਚ ਨਾਲ. ਧਰਤੀ ਉੱਤੇ ਡਿੱਗੇਗੀ। ਪਰੰਤੂ ਇਸ ਦਾ ਆਕਾਰ ਵੀ ਦੁੱਗਣਾ ਹੋਵੇਗਾ। ਨਿਊਟਨ ਦੇ ਦੂਜੇ ਨਿਯਮ ਅਨੁਸਾਰ, ਇਹ ਦੋਵੇਂ ਪ੍ਰਭਾਵ ਇਕ ਦੂਜੇ ਨੂੰ ਰੱਦ ਕਰ ਦਿੰਦੇ ਹਨ, ਇਸ ਲਈ ਸਾਰੇ ਹਾਲਾਤ ਵਿੱਚ, ਰਫ਼ਤਾਰ ਇਕੋ ਜਿੰਨੀ ਰਹੇਗੀ।

ਨਿਊਟਨ ਦਾ ਖਿੱਚ-ਸ਼ਕਤੀ ਦਾ ਗੁਰ ਸਾਨੂੰ ਇਹ ਵੀ ਦੱਸਦਾ ਹੈ ਕਿ ਵਸਤੂਆਂ ਵਿਚਕਾਰ ਦੂਰੀ ਜਿਤਨੀ ਵਧੇਰੇ ਹੋਵੇਗੀ, ਉਨ੍ਹਾਂ ਦੀ ਖਿੱਚ-ਸ਼ਕਤੀ ਘੱਟ ਹੋਵੇਗੀ। ਇਹ ਗੁਰ ਇਹ ਵੀ ਦੱਸਦਾ ਹੈ ਕਿ ਜੇ ਇਕੋ ਜਿਹੇ ਤਾਰਿਆਂ ਵਿਚਕਾਰ ਦੂਰੀ ਅੱਧੀ ਹੋ ਜਾਵੇ ਤਾਂ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਕਤੀ ਇੱਕ ਚੁਥਾਈ ਰਹਿ ਜਾਵੇਗੀ। ਇਹ ਗੁਰ ਧਰਤੀ, ਚੰਦ ਅਤੇ ਹੋਰ ਗ੍ਰਹਿ ਦੇ ਗੇੜਿਆਂ ਦਾ ਸਹੀ-ਸਹੀ ਵੇਰਵਾ ਦਿੰਦਾ ਹੈ। ਜੇ ਗੁਰ ਇਹ ਹੁੰਦਾ ਕਿ ਜੇ ਕਿਸੇ ਇਕ ਤਾਰੇ ਦੀ ਖਿੱਚ ਸ਼ਕਤੀ ਫ਼ਾਸਲਾ ਵਧਣ ਦੇ ਹਿਸਾਬ ਨਾਲ ਘੱਟ ਜਾਵੇਗੀ, ਤਾਂ ਗ੍ਰਹਿ ਦੇ ਗੇੜੇ ਵਿੰਗੇ ਟੇਢੇ (ਫੌੜ ਵਾਲੇ) ਨਾ ਹੁੰਦੇ ਅਤੇ ਉਹੋ ਸਿੱਧੇ ਸੂਰਜ ਵਲ ਧੂਏ ਜਾਂਦੇ। ਜੇ ਉਨ੍ਹਾਂ ਦੀ ਹੇਠਾਂ ਜਾਣ ਦੀ ਰਫ਼ਤਾਰ ਮਠੇਰੀ ਹੁੰਦੀ, ਤਾਂ ਦੂਰ-ਦੁਰਾਡੇ ਤਾਰਿਆਂ ਦੀ ਖਿੱਚ-ਸ਼ਕਤੀ, ਧਰਤੀ ਦੀ ਖਿੱਚ ਨਾਲੋਂ ਅਧਿਕਤਰ ਹੋਣੀ ਸੀ।

ਅਰਸਤੂ ਅਤੇ ਗਲੀਲੀਓ ਤੇ ਨਿਊਟਨ ਦੇ ਵਿਚਾਰਾਂ ਵਿੱਚ ਵੱਡਾ ਅੰਤਰ ਤਾਂ ਇਹ ਹੈ ਕਿ ਅਰਸਤੂ ਦਾ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਕੋਈ ਸ਼ਕਤੀ ਓਨਾ ਚਿਰ ਟਿਕਾਓ ਦੀ ਹਾਲਤ ਵਿੱਚ ਵਿਚਰਨਾ ਪਸੰਦ ਕਰਦੀ ਹੈ, ਜਿਤਨਾ ਚਿਰ ਉਸ ਨੂੰ ਕੋਈ ਹੋਰ ਸ਼ਕਤੀ ਧੱਕਾ ਨਹੀਂ ਦਿੰਦੀ। ਉਸ ਦਾ ਖ਼ਿਆਲ ਤਾਂ ਇਹ ਸੀ ਕਿ ਧਰਤੀ ਟਿਕਾਓ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਹੈ। ਪਰੰਤੂ ਨਿਊਟਨ ਦੇ ਨਿਯਮਾਂ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਟਿਕਾਓ ਦਾ ਕੋਈ ਨਿਵੇਕਲਾ ਪੱਧਰ ਨਹੀਂ ਹੈ। ਫੇਰ ਤਾਂ ਕੋਈ ਕਹਿ ਸਕਦਾ ਹੈ ਕਿ ਵਸਤੂ ‘ਉ’ ਟਿਕਾਓ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਸੀ ਅਤੇ ਵਸਤੂ ‘ਅ’ ਇਕ ਬਨ੍ਹਵੀਂ ਰਫ਼ਤਾਰ ਨਾਲ ਚਲ ਰਹੀ ਸੀ, ਜਾਂ ਵਸਤੂ ‘ਅ’ ਟਿਕਾਓ ਵਿੱਚ ਸੀ ਅਤੇ ਵਸਤੂ ‘ਓ’ ਚੱਲ ਰਹੀ ਸੀ। ਉਦਾਹਰਣ ਵਜੋਂ ਜੇ ਮੰਨ ਲਈਏ ਕਿ ਧਰਤੀ ਟਿਕਾਓ ਵਿੱਚ ਹੈ ਅਤੇ ਇਹ ਸੂਰਜ ਦੁਆਲੇ ਗੇੜੇ ਨਹੀਂ ਕੱਢਦੀ, ਤਾਂ ਇਹ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਧਰਤੀ ਤਾਂ ਟਿਕਾਓ ਵਿੱਚ ਹੈ ਅਤੇ ਇਹ ਕਿ ਇਕ ਰੇਲ ਗੱਡੀ ਧਰਤੀ ਉੱਤੇ ਨੱਬੇ ਮੀਲ ਪ੍ਰਤੀ ਘੰਟਾ ਦੀ ਰਫ਼ਤਾਰ ਨਾਲ ਉੱਤਰ ਵੱਲ ਜਾ ਰਹੀ ਹੈ, ਜਾਂ ਇਹ ਕਿ ਰੇਲ ਗੱਡੀ ਖਲੋਤੀ ਹੈ ਅਤੇ ਧਰਤੀ ਨੱਬੇ ਮੀਲ ਦੀ ਗਤੀ ਨਾਲ ਦੱਖਣ ਵੱਲ ਜਾ ਰਹੀ ਹੈ। ਜੇ ਕੋਈ ਵਸਤੂਆਂ ਸੰਬੰਧੀ ਤਜਰਬੇ ਕਰਕੇ ਦੇਖੀਏ ਤਾਂ ਨਿਊਟਨ ਦੇ ਗੁਰ ਕਾਇਮ ਰਹਿੰਦੇ ਹਨ। ਉਦਾਹਰਣ ਵਜੋਂ, ਰੇਲ ਗੱਡੀ ਵਿੱਚ ਬੈਠਿਆਂ ਪਿੰਗ ਪੌਂਗ ਖੇਡਣ ਵਾਲੇ ਦੇਖਣਗੇ ਕਿ ਗੇਂਦ ਨਿਊਟਨ ਦੇ ਨਿਯਮ ਦੀ ਪਾਲਣਾ ਕਰਦੀ ਹੈ ਜਿਵੇਂ ਟੇਬਲ ਉੱਤੇ ਗੇਂਦ ਚੱਲਦੀ ਹੈ। ਸੋ ਇਹ ਕਹਿਣਾ ਮੁਸ਼ਕਲ ਹੈ ਕਿ ਰੇਲ ਗੱਡੀ ਚੱਲਦੀ ਹੈ, ਜਾਂ ਧਰਤੀ। ਚੀਜ਼ਾਂ ਦੇ ਟਿਕਾਓ ਬਾਰੇ ਪੱਕਾ ਨਿਰਣਾ ਮੌਜੂਦ ਨਾ ਹੋਣ ਕਰਕੇ ਸਾਡੇ ਲਈ ਇਕ ਫ਼ੈਸਲਾ ਕਰ ਸਕਣਾ ਅਸੰਭਵ ਹੈ ਕਿ ਜੇ ਦੋ ਘਟਨਾਵਾਂ ਇਕੋ ਸਮੇਂ ਨਾ ਘਟੀਆਂ ਹੋਣ ਤਾਂ ਪੁਲਾੜ ਵਿੱਚ ਉਨ੍ਹਾਂ ਦਾ ਸਥਾਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਹਾਲਤ ਇੱਕੋ ਜਿਹੀ ਸੀ ਜਾਂ ਨਹੀਂ। ਉਦਾਹਰਣ ਵਜੋਂ ਫ਼ਰਜ਼ ਕਰ ਲਉ ਕਿ ਟਰੇਨ ਵਿੱਚ ਬੈਠਿਆਂ, ਸਾਡੀ ਪਿੰਗ ਪੌਂਗ ਗੇਂਦ ਦੂਜੇ ਪਾਸੇ ਜਾਣ ਵੇਲੇ ਅਤੇ ਉਧਰੋਂ ਮੁੜਨ ਵੇਲੇ ਸਿੱਧੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਇਕ ਸਕਿੰਟ ਦੇ ਵਕਫ਼ੇ ਮਗਰੋਂ, ਮੇਜ਼ ਦੇ ਇਕੋ ਨੁਕਰੇ ਨੂੰ ਛੂੰਹਦੀ ਹੈ। ਰੇਲ ਦੀ ਪਟੜੀ ਉੱਤੇ ਖਲੋਤੇ ਵਿਅਕਤੀ ਨੂੰ ਜਾਪੇਗਾ ਕਿ ਗੇਂਦ ਦੇ ਦੋਵੇਂ ਸਫ਼ਰ ਚਾਲੀ ਮੀਟਰ ਦੀ ਵਿੱਥ ਉੱਤੇ ਵਾਪਰੇ ਹਨ, ਕਿਉਂਕਿ ਦੋਹਾਂ ਸਫ਼ਰਾਂ ਦੇ ਵਕਫ਼ੇ ਵਿੱਚ ਟਰੇਨ ਚਾਲੀ ਮੀਟਰ ਦੂਰ ਚਲੀ ਗਈ ਹੋਵੇਗੀ। ਟਿਕਾਉ ਦਾ ਪੱਕਾ ਆਧਾਰ ਮੌਜੂਦ ਨਾ ਹੋਣ ਕਰਕੇ, ਕੋਈ ਵੀ ਪੁਲਾੜ ਵਿੱਚ ਵਾਪਰੀ ਕਿਸੇ ਵੀ ਘਟਨਾ ਦਾ ਪੱਕਾ ਠੀਹਾ ਨਹੀਂ ਦੱਸ ਸਕਦਾ, ਜਿਵੇਂ ਅਰਸਤੂ ਦਾ ਵਿਸ਼ਵਾਸ ਹੁੰਦਾ ਸੀ। ਘਟਨਾਵਾਂ ਦੇ ਵਾਪਰਨ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਵਿੱਚ ਠੀਹਿਆਂ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿਚਕਾਰਲੇ ਫ਼ਾਸਲਿਆਂ ਨੂੰ ਟਰੇਨ ਵਿੱਚ ਬੈਠੇ ਵਿਅਕਤੀ ਅਤੇ ਪਟੜੀ ਉੱਤੇ ਖਲੋਣ ਵਾਲੇ ਵਿਅਕਤੀ ਵੱਖਰੇ-ਵੱਖਰੇ ਥਾਵਾਂ ਉੱਤੇ ਪ੍ਰਤੀਤ ਹੋਣਗੇ। ਪੇਰ ਦੋਹਾਂ ਦੀਆਂ ਥਾਵਾਂ ਵਿੱਚੋਂ ਕਿਸੇ ਇਕ ਨੂੰ ਵਧੇਰੇ ਸਹੀ ਨਹੀਂ ਮੰਨਿਆ ਜਾਵੇਗਾ।

ਨਿਊਟਨ ਨੂੰ ਕਿਸੇ ਪੱਕੇ ਠਿਕਾਣੇ, ਜਾਂ ਪੁਲਾੜ, ਦੀ ਅਣਹੋਂਦ ਬਹੁਤ ਪਰੇਸ਼ਾਨ ਕਰਦੀ ਸੀ, ਕਿਉਂਕਿ ਇਹ ਅਵਸਥਾ ਉਸ ਦੇ ਇੱਕੋ ਇਕ ਈਸ਼ਵਰ ਵਾਲੇ ਵਿਸ਼ਵਾਸ ਨਾਲ ਮੇਲ ਨਹੀਂ ਸੀ ਖਾਂਦੀ। ਅਸਲ ਵਿੱਚੋਂ, ਉਹ ਨਿਸ਼ਚਿਤ ਪੁਲਾੜੀਂ ਠਿਕਾਣੇ ਦੀ ਅਣਹੋਂਦ ਨੂੰ ਸਵੀਕਾਰ ਨਹੀਂ ਸੀ ਕਰਦਾ, ਭਾਵੇਂ ਉਸ ਦੇ ਆਪਣੇ ਨਿਯਮ ਉਸ ਦੀ ਹਾਮੀਂ ਭਰਦੇ ਸਨ। ਬਹੁਤ ਸਾਰੇ ਲੋਕ ਉਸ ਦੇ ਇਸ ਬੇ-ਤੁਕੇ ਰਵੱਈਏ ਦਾ ਖੰਡਣ ਕਰਦੇ ਸਨ, ਵਿਸ਼ੇਸ਼ ਕਰਕੇ ਪਾਦਰੀ ਬਰਕਲੇ, ਜਿਹੜਾ ਇਸ ਵਿਸ਼ਵਾਸ ਦਾ ਧਾਰਨੀ ਦਾਰਸ਼ਨਿਕ ਸੀ ਕਿ ਸਾਰੇ ਪਦਾਰਥ, ਪੁਲਾੜ ਅਤੇ ਸਮਾਂ ਕੇਵਲ ਇਕ ਭਰਮ ਸਨ ਜਾਂ ਨਿਰਾ ਫ਼ਰੇਬ। ਜਦੋਂ ਬਿਸ਼ਪ ਡਾਕਟਰ ਜਾਨਸਨ ਨੂੰ ਬਰਕਲੇ ਦਾ ਮੱਤ ਦੱਸਿਆ ਗਿਆ, ਤਾਂ ਉਹ ਚਿੱਲਾ ਉੱਠੇ ਸਨ, “ਇਸ ਮਤ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਠੁਕਰਾ ਦਿਉ” ਅਤੇ ਉਸ ਨੇ ਇੱਕ ਵੱਡੇ ਪੱਥਰ ਵਿੱਚ ਠੁੱਡ ਮਾਰ ਦਿੱਤੀ ਸੀ।

ਅਰਸਤੂ ਅਤੇ ਨਿਊਟਨ ਦੋਵੇਂ ਸਮੇਂ ਨੂੰ ਪੱਕਾ ਸਮਝਦੇ ਸਨ। ਅਰਥਾਤ ਉਨ੍ਹਾਂ ਦਾ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਇਕ ਵਿਅਕਤੀ, ਦੋ ਘਟਨਾਵਾਂ ਦੇ ਆਪਸੀ ਸਮਿਆਂ ਦੇ ਵਕਫ਼ੇ ਨੂੰ ਸਹੀ-ਸਹੀ ਮਿਣ ਸਕਦਾ ਹੈ ਅਤੇ ਭਾਵੇਂ ਕੋਈ ਵੀ ਮਿਣ ਕੇ ਦੇਖੇ ਹਰ ਇਕ ਲਈ ਇਹ ਸਮਾਂ ਇਕੋ ਹੋਵੇਗਾ, ਜੇ ਘੜੀ ਹਰ ਪੱਖੋਂ ਚੰਗੀ ਹੋਵੇ। ਸਮਾਂ ਪੁਲਾੜ ਨਾਲੋਂ ਬਿਲਕੁਲ ਵੱਖਰਾ ਹੈ ਅਤੇ ਪੂਰੀ ਤਰ੍ਹਾਂ ਆਜ਼ਾਦ। ਇਹ ਵਿਚਾਰ ਆਮ ਆਦਮੀਆਂ ਦੀ ਸਮਝ ਵਿੱਚ ਆਉਣ ਵਾਲਾ ਸੀ। ਪਰੰਤੂ ਸਾਨੂੰ ਪੁਲਾੜ ਅਤੇ ਸਮੇਂ ਬਾਰੇ ਆਪਣਾ ਵਿਚਾਰ ਬਦਲਣਾ ਪੈ ਗਿਆ ਹੈ। ਭਾਵੇਂ ਜਦੋਂ ਅਸੀਂ ਸੇਬਾਂ ਅਤੇ ਗ੍ਰਹਿ ਵਰਗੀਆਂ ਚੀਜ਼ਾਂ ਨੂੰ ਮੁੱਖ ਰੱਖਦੇ ਹਾਂ, ਤਾਂ ਸਾਨੂੰ ਇਹ ਵਿਚਾਰ ਠੀਕ ਲੱਗਦਾ ਹੈ, ਕਿਉਂਕਿ ਇਹ ਵਸਤਾਂ ਬਹੁਤ ਹੀ ਮੱਠੀ ਚਾਲ ਚਲਦੀਆਂ ਹਨ, ਪਰ ਜਿਹੜੀਆਂ ਵਸਤਾਂ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਚੱਲਦੀਆਂ ਹਨ, ਉਨ੍ਹਾਂ ਪ੍ਰਤੀ ਇਹ ਵਿਚਾਰ ਕਿਸੇ ਕੰਮ ਨਹੀਂ ਆਉਂਦਾ।

ਇਹ ਗੱਲ ਕਿ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਸੀਮਤ, ਪਰੰਤੂ ਬਹੁਤ ਹੀ ਤੇਜ਼ ਹੈ, ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਡੈਨਮਾਰਕ ਦੇ ਤਾਰਕ ਦਾਰਸ਼ਨਿਕ ਓਲ ਕਰਿਸਟਸਨ ਰੋਮਰ (Ole Christensen Roemer) ਨੇ ਮਾਲੂਮ ਕੀਤੀ ਸੀ। ਉਸ ਨੇ ਦੇਖਿਆ ਕਿ ਜੁਪੀਟਰ ਗ੍ਰਹਿ ਦੇ ਦੁਆਲੇ ਘੁੰਮਣ ਵਾਲੇ ਚੰਨਾਂ ਦੇ ਸਮਿਆਂ ਵਿੱਚ ਇਕ-ਸੁਰਤਾ ਨਹੀਂ ਸੀ, ਜੋ ਕੇਵਲ ਉਦੋਂ ਹੀ ਸੰਭਵ ਹੋ ਸਕਦਾ ਸੀ ਜੇ ਉਨ੍ਹਾਂ ਚੰਨਾਂ ਦੇ ਵਿਚਕਾਰਲਾ ਫ਼ਾਸਲਾ ਇਕੋ ਜਿਹਾ ਹੁੰਦਾ। ਜਦੋਂ ਧਰਤੀ ਅਤੇ ਜੁਪੀਟਰ ਸੂਰਜ ਦੁਆਲੇ ਚੱਕਰ ਲਾਉਂਦੇ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਵਿਚਕਾਰ ਫ਼ਾਸਲਾ ਬਦਲਦਾ ਰਹਿੰਦਾ ਹੈ। ਰੋਮਰ ਨੇ ਦੇਖਿਆ ਕਿ ਜੁਪੀਟਰ ਦੇ ਚੰਨਾਂ ਦੇ ਗ੍ਰਹਿਣ ਜਿੰਨੇ ਉਹ ਜੁਪੀਟਰ ਤੋਂ ਦੁਰਾਡੇ ਹੁੰਦੇ ਸਨ, ਉਤਨੇ ਹੀ ਪੱਛੜ ਕੇ ਵਾਪਰਦੇ ਸਨ। ਉਸ ਦੀ ਦਲੀਲ ਇਹ ਸੀ ਕਿ ਕਿਉਂਕਿ ਜਿਤਨੇ ਅਸੀਂ ਚੰਦ ਤੋਂ ਦੂਰ ਹੁੰਦੇ ਹਾਂ, ਰੌਸ਼ਨੀ ਨੂੰ ਸਾਡੇ ਤੱਕ ਪਹੁੰਚਣ ਵਿੱਚ ਉਤਨਾ ਹੀ ਵੱਧ ਸਮਾਂ ਲੱਗਦਾ ਹੈ। ਉਸ ਵੱਲੋਂ ਕੀਤੀਆਂ ਗਈਆਂ ਧਰਤੀ ਤੋਂ ਜੁਪੀਟਰ ਦੇ ਫ਼ਾਸਲੇ ਦੇ ਫ਼ਰਕ ਦੀਆਂ ਮਿਣਤੀਆਂ ਬਹੁਤੀਆਂ ਦਰੁੱਸਤ ਨਹੀਂ ਸਨ, ਇਸ ਲਈ ਉਸ ਦੇ ਹਿਸਾਬ ਅਨੁਸਾਰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ 1,40,000 ਮੀਲ ਪ੍ਰਤੀ ਸਕਿੰਟ ਬਣਦੀ ਹੈ, ਜਿਸ ਦੇ ਟਾਕਰੇ ਵਿੱਚ ਮੌਜੂਦਾ ਰਫ਼ਤਾਰ 1,86,000 ਮੀਲ ਪ੍ਰਤੀ ਸਕਿੰਟ ਮੰਨੀ ਜਾਂਦੀ ਹੈ। ਫੇਰ ਵੀ ਰੋਮਰ ਦੀ ਇਹ ਪ੍ਰਾਪਤੀ ਕਿ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਸੀਮਿਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਰਫ਼ਤਾਰ ਦੀ ਮਿਣਤੀ ਕੀ ਹੈ, ਅਤਿ ਸ਼ਲਾਘਾ-ਯੋਗ ਹੈ ਅਤੇ ਇਹ ਜਾਣਕਾਰੀ ਨਿਊਟਨ ਦੀ ਰਚਨਾ Principia Mathematica ਤੋਂ ਸੱਤ ਸਾਲ ਪਹਿਲਾਂ ਪ੍ਰਾਪਤ ਹੋ ਚੁੱਕੀ ਸੀ।

ਰੌਸ਼ਨੀ ਦੇ ਪ੍ਰਚਾਰ ਸੰਬੰਧੀ ਮੰਨਣ-ਯੋਗ ਸਿਧਾਂਤ 1805 ਈਸਵੀ ਤੋਂ ਪਹਿਲਾਂ ਸਾਹਮਣੇ ਨਹੀਂ ਸੀ ਆਇਆ। ਜਦੋਂ ਤੱਕ ਬਰਤਾਨੀਆਂ ਦੇ ਫਿਜ਼ਿਕਸ ਦੇ ਵਿਗਿਆਨੀ James Clark Maxwell ਨੇ ਅੰਸ਼ਕ ਸਿਧਾਂਤਾਂ ਨੂੰ, ਜਿਹੜੇ ਹੁਣ ਤੱਕ ਵਰਤੇ ਜਾਂਦੇ ਸਨ, ਜੋੜ ਨਹੀਂ ਸੀ ਲਿਆ ਅਤੇ ਜਿਨ੍ਹਾਂ ਦਾ ਸੰਬੰਧ ਬਿਜਲੀ ਅਤੇ ਚੁੰਭਕ ਸ਼ਕਤੀ ਨਾਲ ਹੁੰਦਾ ਸੀ। ਮੈਕਸਵੈਲ ਦੀ ਖੋਜ ਨਾਲ ਪਤਾ ਲੱਗਦਾ ਸੀ ਕਿ ਬਿਜਲੀ ਚੁੰਭਕ ਦੀ ਜੀਵਿਤ ਸ਼ਕਤੀ ਦੇ ਪਿੜ ਵਿੱਚ ਯੁੱਧ ਵਰਗੀਆਂ ਗੜਬੜਾਂ ਪੈਂਦਾ ਹੋ ਸਕਦੀਆਂ ਹਨ ਅਤੇ ਉਹ ਬੰਨਵੀਂ ਰਫ਼ਤਾਰ ਨਾਲ ਚੱਲਣਗੀਆਂ ਜਿਵੇਂ ਟੋਭੇ ਵਿੱਚ ਲਹਿਰਾਂ ਚਲਿਆ ਕਰਦੀਆਂ ਹਨ। ਜੇ ਇਕ ਲਹਿਰ ਦਾ ਦੂਜੀ ਲਹਿਰ ਤੋਂ ਫ਼ਾਸਲਾ ਇਕ ਮੀਟਰ ਹੋਵੇ, ਜਾਂ ਉਸ ਤੋਂ ਅਧਿਕ, ਤਾਂ ਉਨ੍ਹਾਂ ਲਹਿਰਾਂ ਨੂੰ ਅਸੀਂ ਰੇਡੀਓ-ਲਹਿਰਾਂ (Radio waves) ਕਹਿੰਦੇ ਹਾਂ। ਇਸ ਤੋਂ ਘੱਟ ਫ਼ਾਸਲੇ ਵਾਲੀਆਂ ਲਹਿਰਾਂ ਨੂੰ ਅਸੀਂ ਮਾਈਕਰੋ-ਲਹਿਰਾਂ (Micro waves) ਕਹਿੰਦੇ ਹਾਂ। (ਕੁਝ ਸੈਂਟੀਮੀਟਰ, ਜਾਂ ਇਕ ਸੈਂਟੀਮੀਟਰ ਦਾ ਦਸ ਹਜ਼ਾਰਵਾਂ ਹਿੱਸਾ) ਜਿਹੜੀ ਰੌਸ਼ਨੀ ਸਾਨੂੰ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਉਸ ਦੀਆਂ ਲਹਿਰਾਂ ਦਾ ਫ਼ਾਸਲਾ ਇਕ ਸੈਂਟੀਮੀਟਰ ਦੇ ਚਾਰ ਸੌ ਅੱਠ ਕਰੋੜਵੇਂ ਹਿੱਸੇ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ। ਇਸ ਤੋਂ ਵੀ ਘੱਟ ਫ਼ਾਸਲੇ ਵਾਲੀਆਂ ਲਹਿਰਾਂ ਨੂੰ (Ultra Violet) ਐਕਸ-ਰੇਜ਼ ਜਾਂ ਗਾਮਾ (Gamma) ਰੇਜ਼ ਕਹਿੰਦੇ ਹਾਂ।

ਮੈਕਸਵੈਲ ਦੇ ਸਿਧਾਂਤ ਨੇ ਸਿੱਧ ਕਰ ਦਿੱਤਾ ਕਿ ਰੇਡੀਓ ਜਾਂ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਦੇ ਚੱਲਣ ਦੀ ਰਫ਼ਤਾਰ ਬੰਨ੍ਹਵੀਂ ਹੋਇਆ ਕਰਦੀ ਹੈ। ਪਰੰਤੂ ਨਿਊਟਨ ਪੱਕੇ ਟਿਕਾਓ ਵਾਲੇ ਸਿਧਾਂਤ ਤੋਂ ਸੁਰਖਰੂ ਹੋ ਗਿਆ ਸੀ। ਇਸ ਲਈ ਜੇ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਬੰਨ੍ਹਵੀਂ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਸ ਬੰਨ੍ਹਵੀਂ ਰਫ਼ਤਾਰ ਦੀ ਮਿਣਤੀ ਵੀ ਹੋ ਸਕਦੀ ਸੀ। ਇਸ ਲਈ ਇਹ ਸਮਝਿਆ ਜਾਣ ਲੱਗ ਪਿਆ ਕਿ ਇਕ ਪਦਾਰਥ ਜਿਸ ਨੂੰ Ether ਕਹਿੰਦੇ ਹਨ, ਹਰ ਇਕ ਥਾਂ ਮੌਜੂਦ ਹੈ, ਇੱਥੋਂ ਤੱਕ ਕਿ ਖ਼ਾਲੀ ਪੁਲਾੜ ਵਿੱਚ ਵੀ। ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਨੂੰ Ether ਵਿੱਚੀ ਲੰਘਣਾ ਪੈਂਦਾ ਹੈ, ਜਿਵੇਂ ਆਵਾਜ਼ ਦੀਆਂ ਲਹਿਰਾਂ ਹਵਾ ਵਿੱਚੋਂ ਲੰਘਦੀਆਂ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਰਫ਼ਤਾਰ ਦਾ ਅਨੁਪਾਤ Ether ਅਨੁਸਾਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਵੱਖਰੇ-ਵੱਖਰੇ ਦੇਖਣ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਨੂੰ Ether ਅਨੁਸਾਰ ਚੱਲਣ ਵੇਲੇ, ਐਉਂ ਅਨੁਭਵ ਹੋਵੇਗਾ ਕਿ ਰੌਸ਼ਨੀ ਉਨ੍ਹਾਂ ਵੱਲ ਵੱਖਰੀਆਂ ਰਫ਼ਤਾਰਾਂ ਨਾਲ ਆ ਰਹੀ ਹੈ, ਪਰੰਤੂ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ Ether ਅਨੁਸਾਰ ਬੰਨ੍ਹਵੀਂ ਅਤੇ ਇਕੋ ਜਿਹੀ ਰਹੇਗੀ। ਵਿਸ਼ੇਸ਼ ਕਰਕੇ, ਕਿਉਂਕਿ ਧਰਤੀ Ether ਵਿੱਚੀਂ ਲੰਘ ਕੇ, ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮਦੀ ਹੈ, ਇਸ ਲਈ ਰੌਸ਼ਨੀ ਦੀ ਧਰਤੀ ਵੱਲ ਆਉਣ ਦੀ ਰਫ਼ਤਾਰ Ether ਵਿਚੀਂ ਹੋ ਕੇ, ਜਦੋਂ ਅਸੀਂ ਰੌਸ਼ਨੀ ਦੇ ਸੋਮੇ ਵੱਲ ਜਾਈਏ, ਤਾਂ ਇਹ ਰਫ਼ਤਾਰ ਰੌਸ਼ਨੀ ਦੀ ਉਸ ਰਫ਼ਤਾਰ ਨਾਲੋਂ ਅਧਿਕ ਹੋਵੇਗੀ। ਜਦੋਂ ਅਸੀਂ ਰੌਸ਼ਨੀ ਦੇ ਸੋਮੇ ਵੱਲ 90° ਬਣਾ ਕੇ ਵੱਧ ਨਹੀਂ ਰਹੇ ਹੋਵਾਂਗੇ। 1887 ਈਸਵੀ ਵਿੱਚ ਅਲਬਰਟ ਮਾਈਕਾਲਸਨ, (Albert Michelson) ਜਿਹੜੇ ਫਿਜ਼ਿਕਸ ਲਈ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਨੋਬਲ ਪੁਰਸਕਾਰ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੇ ਅਮ੍ਰੀਕਨ ਸਨ ਅਤੇ (Edward Morley) ਐਡਵਰਡ ਮੌਰਲੀ ਨੇ (Cleveland) ਕਲੀਵਲੈਂਡ ਦੇ (Applied Science) ਦੇ ਕੇਸ ਸਕੂਲ ਵਿੱਚ ਕੁਝ ਕਾਰਆਮਦ ਤਜਰਬੇ ਕੀਤੇ ਸਨ। ਉਨ੍ਹਾਂ ਨੇ ਧਰਤੀ ਵੱਲ ਆਉਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਦਾ ਉਸ ਰਫ਼ਤਾਰ ਨਾਲ ਟਾਕਰਾ ਕੀਤਾ, ਜੋ ਧਰਤੀ ਵੱਲ ਨੂੰ ਐਨ ਸਿੱਧੀ ਸੇਧ (90°) ਕੋਣ ਵਾਲੀ ਸੀ। ਜਦੋਂ ਉਨ੍ਹਾਂ ਨੇ ਦੇਖਿਆ ਕਿ ਉਹ ਦੋਵੇਂ ਰਫ਼ਤਾਰਾਂ ਐਨ ਬਰਾਬਰ ਸਨ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੀ ਹੈਰਾਨੀ ਦੀ ਹੱਦ ਨਾ ਰਹੀ।

1887 ਅਤੇ 1905 ਈਸਵੀ ਦੇ ਵਿਚਕਾਰ, (Michelson) ਮੌਰਲੀ ਦੇ ਤਜਰਬਿਆਂ ਦੀ ਵਿਆਖਿਆ ਕਰਨ ਲਈ ਬਹੁਤ ਕੋਸ਼ਿਸ਼ਾਂ ਕੀਤੀਆਂ ਗਈਆਂ ਸਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਹਾਲੈਂਡ ਦੇ ਫਿਜ਼ਿਕਸ ਵਿਗਿਆਨੀ (Hendrik Lorentz) ਹੈਨਰਿਕ ਲੋਰੈਂਜ਼ ਦੀ ਕੋਸ਼ਿਸ਼ ਵਿਸ਼ੇਸ਼ ਤੌਰ ‘ਤੇ ਵਰਨਣ-ਯੋਗ ਹੈ। ਉਨ੍ਹਾਂ ਨੇ ਈਥਰ Ether ਵਿੱਚੀਂ ਲੰਘਣ ਵਾਲੀਆਂ ਵਸਤਾਂ, ਜੋ ਸੁੰਗੜ ਜਾਂਦੀਆਂ ਸਨ ਅਤੇ ਕਲਾਕ ਉਸ ਵੇਲੇ ਰਫ਼ਤਾਰ ਵਿੱਚ ਹੌਲੀ ਹੋ ਜਾਂਦੇ ਸਨ, ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਤਜਰਬਿਆਂ ਬਾਰੇ ਵਿਆਖਿਆ ਕੀਤੀ ਸੀ। ਪਰੰਤੂ 1905 ਈਸਵੀ ਵਿੱਚ ਸਵਿਟਜ਼ਰਲੈਂਡ ਦੇ Patent Office ਦੇ ਗੁੰਮਨਾਮ ਜਿਹੇ ਕਲਰਕਾਂ Albert Einstein ਨੇ ਰਾਏ ਦਿੱਤੀ ਕਿ Ether ਵਾਲੇ ਵਿਚਾਰ ਦੀ ਲੋੜ ਹੀ ਨਹੀਂ, ਜੇ ਕੋਈ ਨਿਸ਼ਚਿਤ (ਪੱਕੇ) ਸਮੇਂ ਦੇ ਵਿਚਾਰ ਨੂੰ ਤਿਆਗਣ ਲਈ ਰਜ਼ਾਮੰਦ ਹੋ ਜਾਵੇ। ਇਸੇ ਪ੍ਰਕਾਰ ਦਾ ਵਿਚਾਰ ਕੁਝ ਹੀ ਹਫ਼ਤਿਆਂ ਮਗਰੋਂ ਫ਼ਰਾਂਸ ਦੇ ਗਣਿਤ ਵਿਗਿਆਨੀ Henri Poincare ਨੇ ਵੀ ਪੇਸ਼ ਕਰ ਦਿੱਤਾ ਸੀ। ਆਈਨ ਸਟਾਈਨ ਦੀਆਂ ਦਲੀਲਾਂ, ਪੁਆਇਨਕੇਰ ਦੀਆਂ ਦਲੀਲਾਂ ਨਾਲੋਂ ਵਧੇਰੇ ਢੁੱਕਵੀਆਂ ਸਨ, ਜਿਹੜੇ ਇਸ ਸਮੱਸਿਆ ਨੂੰ ਗਣਿਤ- ਰੂਪੀ ਸਮਝਦੇ ਸਨ। ਨਵੇਂ ਸਿਧਾਂਤ ਦੇ ਮਾਮਲੇ ਵਿੱਚ ਆਈਨ ਸਟਾਈਨ ਨੂੰ ਵਧੇਰੇ ਮਾਨਤਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ। ਪਰ ਪੁਆਈਨਕੇਰ ਨੂੰ ਵੀ ਇਸ ਸਿਧਾਂਤ ਦੇ ਭਾਈਵਾਲ ਵਜੋਂ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।

ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਦਾ ਮੁੱਢਲਾ ਗੁਣ ਇਹ ਹੈ ਕਿ ਵਿਗਿਆਨ ਦੇ ਸਾਰੇ ਨਿਯਮਾਂ ਨੂੰ ਆਪ-ਮੁਹਾਰੀਆਂ ਚੱਲਣ ਵਾਲੀਆਂ ਵਸਤਾਂ ਲਈ ਇਕੋ ਅਤੇ ਬਰਾਬਰ ਸਮਝਣਾ ਚਾਹੀਦਾ ਹੈ, ਭਾਵੇਂ ਉਨ੍ਹਾਂ ਦੀਆਂ ਰਫ਼ਤਾਰਾਂ ਕੁਝ ਵੀ ਹੋਣ। ਚਾਲ ਸੰਬੰਧੀ ਤਾਂ ਨਿਊਟਨ ਦੇ ਨਿਯਮ ਸੱਚੇ ਹਨ, ਪਰੰਤੂ ਅੱਜ ਕੱਲ੍ਹ, ਮੈਕਸਵੈਲ ਦੇ ਸਿਧਾਂਤ ਨੂੰ ਵੀ ਉਨ੍ਹਾਂ ਨਿਯਮਾਂ ਵਿੱਚ ਸ਼ਾਮਿਲ ਕਰ ਲਿਆ ਗਿਆ ਹੈ ਅਤੇ ਰਫ਼ਤਾਰ ਦੇ ਸਿਧਾਂਤ ਨੂੰ ਵੀ। ਭਾਵੇਂ ਸਾਰੇ ਦਾਰਸ਼ਨਿਕਾਂ ਨੂੰ ਰਫ਼ਤਾਰ ਦਾ ਨਾਪ ਇਕੋ ਜਿਹਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਭਾਵੇਂ ਉਨ੍ਹਾਂ ਦੀ ਰਫ਼ਤਾਰ ਕਿੰਨੀ ਵੀ ਤੇਜ਼ ਹੋਵੇ। ਇਸ ਸਾਧਾਰਣ ਜਿਹੇ ਵਿਚਾਰ ਦੇ ਨਤੀਜੇ ਅਤਿ ਵੱਡਮੁੱਲੇ ਹਨ। ਸ਼ਾਇਦ ਸਭ ਤੋਂ ਕੀਮਤੀ ਨਤੀਜਾ, ਆਕਾਰ ਅਤੇ ਬਿਜਲੀ ਦੀ ਬਰਾਬਰ ਮਾਤਰਾ ਵਾਲਾ ਹੈ, ਜੋ ਆਈਨ ਸਟਾਈਨ ਦੇ ਬਰਾਬਰੀ ਦੇ ਗੁਰ ਵਿੱਚ ਦਰਜ ਹੈ, ਇਹ ਗੁਰ E mc’ ਹੈ, ਜਿਸ ਵਿੱਚ E ਬਿਜਲੀ ਲਈ ਹੈ, M ਆਕਾਰ ਲਈ ਅਤੇ C.ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਲਈ ਵਰਤਿਆ ਗਿਆ ਹੈ ਅਤੇ ਇਹ ਨਤੀਜਾ (ਨਿਯਮ) ਕਿ ਰੌਸ਼ਨੀ ਨਾਲੋਂ ਕਿਸੇ ਵੀ ਹੋਰ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਵੱਧ ਨਹੀਂ ਹੋ ਸਕਦੀ। ਕਿਉਂਕਿ ਬਿਜਲੀ ਅਤੇ ਆਕਾਰ ਬਰਾਬਰ ਹੋਣ ਦੀ ਸੂਰਤ ਵਿੱਚ, ਉਸ ਵਸਤੂ ਵਿਚਲੀ ਬਿਜਲੀ, ਰਫ਼ਤਾਰ ਫੜਨ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਉਸ ਵਸਤੂ ਦੇ ਆਕਾਰ ਵਿੱਚ ਵਾਧਾ ਕਰ ਦਿੰਦੀ ਹੈ ਅਤੇ ਨਤੀਜੇ ਵਜੋਂ ਉਸ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਵਿੱਚ ਵਾਧਾ ਨਹੀਂ ਹੋ ਸਕਦਾ। ਅਜਿਹਾ ਪ੍ਰਭਾਵ ਉਨ੍ਹਾਂ ਵਸਤਾਂ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਹੋਇਆ ਕਰਦਾ ਹੈ, ਜਿਹੜੀਆਂ ਵਸਤਾਂ ਦੀ ਰਫ਼ਤਾਰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ। ਉਦਾਹਰਣ ਵਜੋਂ, ਜੇ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਦੇ 10 ਪ੍ਰਤੀਸ਼ਤ ਹੋਣ ਵੇਲੇ ਉਸ ਵਸਤੂ ਦੇ ਆਕਾਰ ਵਿੱਚ, ਸਾਧਾਰਣ ਆਕਾਰ ਵਿੱਚ ਕੇਵਲ 0.5 ਪ੍ਰਤੀਸ਼ਤ ਵਾਧਾ ਹੋ ਸਕਦਾ ਹੈ, ਪਰੰਤੂ ਜੇ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ 90 ਪ੍ਰਤੀਸ਼ਤ ਹੋਵੇ, ਤਾਂ ਆਕਾਰ ਸਾਧਾਰਣ ਆਕਾਰ ਨਾਲੋਂ ਦੁੱਗਣੇ ਤੋਂ ਵੱਧ ਜਾਵੇਗਾ। ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਦੇ ਨੇੜੇ ਪਹੁੰਚਦੀ ਹੈ, ਤਾਂ ਉਸ ਵਸਤੂ ਦਾ ਆਕਾਰ ਹੋਰ ਵੀ ਤੇਜ਼ੀ ਨਾਲ ਵੱਧਣ ਲੱਗ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਨੂੰ ਅੱਗੇ ਲੈ ਜਾਣ ਲਈ ਵਾਧੂ ਬਿਜਲਈ ਸ਼ਕਤੀ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ। ਅਸਲ ਵਿੱਚ ਕਿਸੇ ਵੀ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਜਿਤਨੀ ਨਹੀਂ ਹੋ ਸਕਦੀ, ਕਿਉਂਕਿ ਉਸ ਵੇਲੇ ਤੱਕ ਇਸ ਦਾ ਆਕਾਰ ਸੀਮਾ-ਰਹਿਤ ਹੋ ਜਾਵੇਗਾ ਅਤੇ ਇਸ ਦੇ ਆਕਾਰ ਅਤੇ ਸ਼ਕਤੀ ਬਰਾਬਰ ਹੋ. ਜਾਣ ਤੇ, ਉਸ ਰਫ਼ਤਾਰ ‘ਤੇ ਪਹੁੰਚਣ ਲਈ ਅਸੀਮ ਸ਼ਕਤੀ ਦੀ ਲੋੜ ਪਵੇਗੀ। ਇਹੋ ਕਾਰਨ ਹੈ ਕਿ ਹਰ ਇਕ ਸਾਧਾਰਣ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਹਿਸਾਬ ਸਿਰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਨਾਲੋਂ ਮਠੇਰੀ ਹੀ ਰਹਿੰਦੀ ਹੈ। ਕੇਵਲ ਰੌਸ਼ਨੀ ਜਾਂ ਹੋਰ ਆਕਾਰ-ਰਹਿਤ ਲਹਿਰਾਂ ਹੀ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਫੜ ਸਕਦੀਆਂ ਹਨ।

ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਦਾ ਇਕ ਗਿਣਤੀ ਯੋਗ ਨਤੀਜਾ ਇਹ ਵੀ ਹੈ ਕਿ ਇਸ ਨਾਲ ਸਾਡੇ ਦੇਸ਼ ਅਤੇ ਕਾਲ ਬਾਰੇ ਵਿਚਾਰਾਂ ਵਿੱਚ ਪ੍ਰੀਵਰਤਨ ਆ ਗਿਆ ਹੈ। ਨਿਊਟਨ ਦੇ ਸਿਧਾਂਤ ਅਨੁਸਾਰ, ਜੇ ਰੌਸ਼ਨੀ ਦੀ ਇਕ ਲਿਸ਼ਕੋਰ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਭੇਜੀ ਜਾਵੇ, ਤਾਂ ਵੱਖੋ-ਵੱਖਰੇ ਦਰਸ਼ਕ ਇਸ ਗੱਲ ‘ਤੇ ਸਹਿਮਤ ਹੋ ਜਾਣਗੇ ਕਿ ਉਸ ਲਿਸ਼ਕੋਰ ਨੇ ਕਿਤਨਾ ਸਮਾਂ ਲਿਆ ਹੈ (ਕਿਉਂਕਿ ਸਮਾਂ ਤਾਂ ਨਿਸ਼ਚਿਤ ਹੈ, ਪਰੰਤੂ ਉਹ ਇਹ ਮੰਨਣ ਲਈ ਸਹਿਮਤ ਨਹੀਂ ਹੋਣਗੇ ਕਿ ਉਸ ਲਿਸ਼ਕੋਰ ਨੇ ਪੈਂਡਾ ਕਿਤਨਾ ਤੈਅ ਕੀਤਾ ਹੈ (ਕਿਉਂਕਿ ਪੁਲਾੜ ਨਿਸ਼ਚਿਤ ਨਹੀਂ ਹੈ)। ਕਿਉਂਕਿ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਤੈਅ ਕੀਤੇ ਫ਼ਾਸਲੇ ਉਸ ਨੂੰ ਲੱਗੇ ਸਮੇਂ ਨਾਲ ਵੰਡਣ ਨਾਲ ਕੱਢੀ ਜਾ ਸਕਦੀ ਹੈ, ਇਸ ਲਈ ਵੱਖਰੇ- ਵੱਖਰੇ ਦਰਸ਼ਕਾਂ ਨੂੰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਵੱਖਰੀ-ਵੱਖਰੀ ਪ੍ਰਤੀਤ ਹੋਵੇਗੀ। ਇਸ ਲਈ ਫ਼ਾਸਲਾ ਤੈਅ ਕਰਨ ਵਿੱਚ ਲੱਗੇ ਸਮੇਂ ਬਾਰੇ ਵੀ ਉਹ ਸਹਿਮਤ ਨਹੀਂ ਹੋਣਗੇ। ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਅਨੁਸਾਰ, ਦੂਜੇ ਬੰਨੇ ਸਾਰੇ ਦੇ ਸਾਰੇ ਦਰਸ਼ਕ ਇਸ ਗੱਲ ਉੱਤੇ ਸਹਿਮਤ ਹੋ ਜਾਣਗੇ ਕਿ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਕਿਤਨੀ ਹੁੰਦੀ ਹੈ। ਪਰੰਤੂ ਉਹ ਹਾਲੇ ਵੀ ਉਸ ਫ਼ਾਸਲੇ ਬਾਰੇ ਸਹਿਮਤ ਨਹੀਂ ਹੋਣਗੇ, ਜਿਹੜਾ ਰੌਸ਼ਨੀ ਨੇ ਤੈਅ ਕੀਤਾ ਹੈ। ਇਸ ਲਈ ਉਹ ਉਸ ਸਮੇਂ ਬਾਰੇ ਵੀ ਸਹਿਮਤ ਨਹੀਂ ਹੋਣਗੇ। ਜਿਹੜਾ ਰੌਸ਼ਨੀ ਨੇ ਫ਼ਾਸਲਾ ਤੋਅ ਕਰਨ ਵਿੱਚ ਲਿਆ ਹੈ। (ਸਮਾਂ ਨਿਸ਼ਚਿਤ ਕਰਨ ਲਈ ਉਹ ਫ਼ਾਸਲਾ ਹੁੰਦਾ ਹੈ ਜੋ ਰੌਸ਼ਨੀ ਨੇ ਤੈਅ ਕੀਤਾ ਹੈ-ਜਿਸ ਬਾਰੇ ਦਰਸ਼ਕ ਸਹਿਮਤ ਨਹੀਂ ਹੁੰਦੇ, ਉਸ ਨੂੰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਨਾਲ ਵੰਡਣਾ ਪੈਂਦਾ ਹੈ, ਜਿਸ ਉੱਤੇ ਦਰਸ਼ਕ ਸਹਿਮਤ ਹਨ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਨੇ ਸਮੇਂ ਦੇ ਨਿਸ਼ਚਿੰਤ ਹੋਣ ਵਾਲੇ ਵਿਚਾਰ ਨੂੰ ਰੱਦ ਕਰ ਦਿੱਤਾ ਹੈ। ਐਉਂ ਜਾਪਦਾ ਹੈ, ਕਿ ਹਰ ਇਕ ਦਰਸ਼ਕ ਕੋਲ ਸਮਾਂ ਨਾਪਣ ਦਾ ਆਪਣਾ-ਆਪਣਾ ਨਾਪ ਹੋਣਾ। ਚਾਹੀਦਾ ਹੈ, ਜਿਹੜਾ ਉਸ ਦੀ ਘੜੀ ਪ੍ਰਗਟ ਕਰਦੀ ਹੋਵੇ ਅਤੇ ਇਹ ਕਿ ਦਰਸ਼ਕਾਂ ਕੋਲ ਜੇ ਇਕੋ ਜਿਹੜੀਆਂ ਘੜੀਆਂ ਹੋਣ ਤਾਂ ਵੀ ਉਨ੍ਹਾਂ ਦੇ ਪ੍ਰਗਟ ਸਮੇਂ ਬਰਾਬਰ ਨਹੀਂ ਹੋ ਸਕਦੇ।

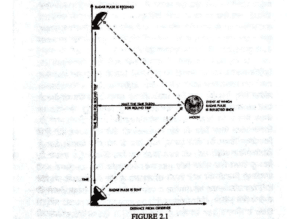
ਸਮਾਂ ਹੇਠ ਤੋਂ ਉੱਪਰ ਵੱਲ ਖਲੋਤੀ ਰੇਖਾ ਮਿਣਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਦਰਸ਼ਕ ਤੋਂ ਦੂਰੀ ਖੱਬਿਓਂ ਸੱਜੇ ਲੇਟਵੀਂ ਰੇਖਾ ਨਾਲ ਮਿਣਿਆ ਜਾਂਦਾ ਹੈ। ਦਰਸ਼ਕ ਦਾ ਰਸਤਾ ਰਾਡਾਰ ਦੀ ਨਬਜ਼ ਦੀ ਲਿਸ਼ਕ ਬਿੰਦੂ ਤੋਂ ਟੇਢੀਆਂ ਰੇਖਾਵਾਂ ਦੁਆਰਾ, ਦਿਖਾਇਆ ਗਿਆ ਹੈ।

ਹਰ ਇਕ ਦਰਸ਼ਕ ਅਜਿਹੇ ਰਾਡਾਰ ਦੀ ਵਰਤੋਂ ਕਰ ਸਕਦਾ ਹੈ, ਜਿਸ ਤੋਂ ਪਤਾ ਲਗ ਸਕੇ ਕਿ ਕੋਈ ਘਟਨਾ ਕਿੱਥੇ ਅਤੇ ਕਦੋਂ ਵਾਪਰੀ ਹੈ। ਅਜਿਹਾ ਕਰਨ ਲਈ ਉਸ ਨੂੰ ਰੌਸ਼ਨੀ ਦੀ ਲਿਸ਼ਕੋਰ ਜਾਂ ਰੇਡੀਆਈ ਲਹਿਰ ਭੇਜਣੀ ਪਵੇਗੀ। ਅਜਿਹੀ ਲਿਸ਼ਕੋਰ ਅੰਸ਼ਕ ਤੌਰ ‘ਤੇ ਉਸ ਥਾਂ ਅਨੁਭਵ ਕੀਤੀ ਜਾਵੇਗੀ, ਜਿੱਥੋਂ ਭੇਜੀ ਗਈ ਸੀ ਅਤੇ ਦਰਸ਼ਕ ਉਸ ਵੇਲੇ ਆਵਾਜ਼ ਸੁਣਨ ਸਾਰ ਸਮਾਂ ਨਾਪ ਸਕਦਾ ਹੈ। ਘਟਨਾ ਵਾਪਰਨ ਦਾ ਸਮਾਂ ਲਿਸ਼ਕੋਰ ਭੇਜਣ ਅਤੇ ਮੁੜਵੀਂ ਲਿਸ਼ਕ ਦੇ ਸਮੇਂ ਦੇ ਅੱਧ ਦੇ ਬਰਾਬਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ। ਫ਼ਾਸਲਾ ਇਸ ਪੂਰੇ ਮੁੜਵੇਂ ਸਮੇਂ ਦੇ ਅੱਧ ਦੇ ਬਰਾਬਰ ਹੋਇਆ ਕਰਦਾ ਹੈ, ਜਿਸ ਨੂੰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਨਾਲ ਗੁਣਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। (ਇਸ ਪੱਖ ਤੋਂ ਘਟਨਾ ਪੁਲਾੜ ਵਿੱਚ, ਕਿਸੇ ਇਕੱਲੇ ਬਿੰਦੂ ਉੱਤੇ ਘਟਿਆ ਕਰਦੀ ਹੈ ਅਤੇ ਸਮੇਂ ਦੇ ਨਿਸ਼ਚਿਤ ਪਲ ਉੱਤੇ)। ਇਹ ਗੁਰ ਤਸਵੀਰ ਨੰ. 2.1 ਵਿੱਚ ਸਿੱਧ ਕੀਤਾ ਗਿਆ ਹੈ, ਜਿਹੜੀ ਪੁਲਾੜ ਸਮੇਂ ਦੇ ਨਕਸ਼ੇ ਦੀ ਉਦਾਹਰਣ ਹੈ। ਇਹ ਨਤੀਜਾ ਵਰਤਣ ਵਾਲੇ ਦਰਸ਼ਕ, ਜੋ ਇਕ-ਦੂਜੇ ਨਾਲ ਸੰਬੰਧ ਕਾਇਮ ਰੱਖ ਕੇ ਚੱਲਣਗੇ, ਉਹ ਉਸ ਘਟਨਾ ਦੇ ਵੱਖਰੇ ਸਮੇਂ ਅਤੇ ਵੱਖਰੀਆਂ ਸਥਿਤੀਆਂ ਦੱਸਣਗੇ। ਕਿਸੇ ਇਕ ਦਰਸ਼ਕ ਦਾ ਨਾਪ, ਕਿਸੇ ਦੂਜੇ ਦਰਸ਼ਕ ਦੇ ਨਾਪ ਨਾਲੋਂ ਵਧੇਰੇ ਸਹੀ ਨਹੀਂ ਮੰਨਿਆ ਜਾ ਸਕਦਾ, ਪਰੰਤੂ ਸਾਰੇ ਨਾਪ ਆਪੋ ਵਿੱਚ ਜੁੜੇ ਹੋਏ ਹਨ। ਇਕ ਦਰਸ਼ਕ, ਦੂਜੇ ਦਰਸ਼ਕ ਵੱਲੋਂ ਘਟਨਾ ਪ੍ਰਤੀ ਮਿੱਥੇ ਸਮੇਂ ਅਤੇ ਸਥਿਤੀ ਦਾ ਪੂਰਾ ਅੰਦਾਜ਼ਾ ਲਾ ਸਕਦਾ ਹੈ, ਜੇ ਦੂਜੇ ਦਰਸ਼ਕ ਦੀ ਰਫ਼ਤਾਰ ਜਾਣਦਾ ਹੋਵੇ।

ਅੱਜ ਕੱਲ੍ਹ ਅਸੀਂ ਫ਼ਾਸਲਿਆਂ ਦੀ ਸਹੀ ਮਿਣਤੀ ਲਈ ਇਹੋ ਢੰਗ ਵਰਤਦੇ ਹਾਂ, ਕਿਉਂਕਿ ਅਸੀਂ ਫ਼ਾਸਲੇ ਦੀ ਲੰਬਾਈ ਨਾਲੋਂ ਸਮੇਂ ਦੀ ਮਿਣਤੀ ਜ਼ਿਅਆਦਾ ਨਹੀਂ ਮਿਣ ਸਕਦੇ ਹਾਂ। ਅਸਲ ਵਿੱਚ ਰੌਸ਼ਨੀ ਵੱਲੋਂ ਜਿਹੜਾ ਫ਼ਾਸਲਾ 0.000000003335640 ਸਕਿੰਟਾਂ ਵਿੱਚ ਤੈਅ ਹੋਵੇ, ਉਹ ਇਕ ਮੀਟਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ। ਜੇ ਉਸ ਦੀ ਮਿਣਤੀ Cesium ਕਲਾਕ ਨਾਲ ਕੀਤੀ ਜਾਵੇ। (ਇਸ ਅੰਕ ਨੂੰ ਵਿਸ਼ੇਸ਼ ਤੌਰ ‘ਤੇ ਮੰਨਣ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਇਸ ਨਾਲ ਮੀਟਰ ਦੀ ਇਤਿਹਾਸਿਕ ਪਰਿਭਾਸ਼ਾ ਹੋ ਜਾਂਦੀ ਹੈ, ਜਿਹੜਾ ਮੀਟਰ ਪੈਰਿਸ ਵਿੱਚ ਰੱਖੇ ਹੋਏ Platinum ਦੀ ਰੱਖੀ ਹੋਈ ਵਿਸ਼ੇਸ਼ ਫੱਟੀ ਉੱਤੇ ਵਿਖਾਇਆ ਗਿਆ ਹੈ।) ਇਸੇ ਪ੍ਰਕਾਰ, ਅਸੀਂ ਇਸ ਤੋਂ ਵੀ ਸੌਖੀ ਇਕਾਈ ਜਿਸ ਨੂੰ ਰੌਸ਼ਨੀ-ਸਕਿੰਟ- ਕਹਿੰਦੇ ਹਨ, ਵੀ ਵਰਤ ਸਕਦੇ ਹਾਂ। ਇਹ ਇਕਾਈ ਉਹ ਫ਼ਾਸਲਾ ਹੈ, ਜਿਸ ਨੂੰ ਰੌਸ਼ਨੀ ਇਕ ਸਕਿੰਟ ਵਿੱਚ ਮੁਕਾ ਲਵੇ। ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਅਨੁਸਾਰ, ਅਸੀਂ ਫ਼ਾਸਲੇ ਦੀ ਮਿਣਤੀ ਸਮੇਂ ਅਤੇ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਮੁੱਖ ਰੱਖ ਕੇ ਕਰਦੇ ਹਾਂ। ਇਸ ਲਈ ਇਹ ਗੱਲ ਆਪਣੇ ਆਪ ਸਪੱਸ਼ਟ ਹੋ ਜਾਂਦੀ ਹੈ ਕਿ ਹਰ ਇਕ ਦਰਸ਼ਕ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਇੱਕੋ ਦੱਸੇਗਾ, (ਇਕ ਮੀਟਰ ਪ੍ਰਤੀ 0.000000003335640952 ਸਕਿੰਟ)। Ether ਦਾ ਵਿਚਾਰ ਕਰਨ ਦੀ ਲੋੜ ਹੀ ਨਹੀਂ ਹੈ, ਕਿਉਂਕਿ ਉਸ ਦੀ ਹੋਂਦ ਦਾ ਪਤਾ ਹੀ ਨਹੀਂ ਲੱਗ ਸਕਦਾ, ਜਿਵੇਂ ਕਿ Michelson-Morley ਦੇ ਤਜਰਬੇ ਤੋਂ ਸਿੱਧ ਹੋ ਚੁੱਕਾ ਹੈ। ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਸਾਨੂੰ ਪੁਲਾੜ ਅਤੇ ਸਮੇਂ ਨਾਲ ਬਣੇ ਵਿਚਾਰਾਂ ਨੂੰ ਬਦਲਣ ਲਈ ਮਜਬੂਰ ਜ਼ਰੂਰ ਕਰਦਾ ਹੈ। ਸਾਨੂੰ ਇਹ ਗੱਲ ਮੰਨ ਹੀ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ ਕਿ ਸਮੇਂ ਨੂੰ ਪੁਲਾੜ ਤੋਂ ਨਾ ਨਿਖੇੜਿਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਨਾ ਹੀ ਸਮਾਂ ਪੁਲਾੜ ਤੋਂ ਆਜ਼ਾਦ ਹੋ ਸਕਦਾ ਹੈ, ਸਗੋਂ ਇਹ ਤਾਂ ਉਸ ਨਾਲ ਜੁੜਿਆ ਹੋਇਆ ਹੈ ਅਤੇ ਨਤੀਜੇ ਵਜੋਂ ਪੁਲਾੜ ਸਮਾਂ ਪ੍ਰਵਾਨ ਹੁੰਦਾ ਹੈ।

ਇਹ ਗੱਲ ਬੜੀ ਸਾਧਾਰਣ ਹੈ ਕਿ ਪੁਲਾੜ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ਦੀ ਵਿਆਖਿਆ ਤਿੰਨ ਅੰਕਾਂ ਜਾਂ ਜੋੜਾਂ ਨਾਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਉਦਾਹਰਣ ਵਜੋਂ, ਕੋਈ ਕਹਿ ਸਕਦਾ ਹੈ ਕਿ ਇਕ ਕਮਰੇ ਦਾ ਇਕ ਬਿੰਦੂ, ਇਕ ਕੰਧ ਤੋਂ ਸੱਤ ਫੁੱਟ ਦੂਰ ਹੈ, ਦੂਜੀ ਕੰਧ ਤੋਂ ਤਿੰਨ ਫੁੱਟ ਅਤੇ ਫ਼ਰਸ਼ ਤੋਂ ਪੰਜ ਫੁੱਟ ਉੱਚਾ ਹੈ। ਜਾਂ ਕੋਈ ਕਹਿ ਸਕਦਾ ਹੈ ਕਿ ਇਕ ਬਿੰਦੂ ਸਾਗਰ ਡੱਟ ਤੋਂ ਉੱਤਰ-ਪੂਰਬ ਵੱਲ ਕਿਤਨੀ ਦੂਰ ਹੈ, ਪੂਰਬ-ਪੱਛਮ ਵੱਲ ਕਿਤਨੀ ਦੂਰ ਅਤੇ ਸਾਗਰ-ਤੱਟ ਤੋਂ ਕਿਤਨਾ ਉੱਚਾ ਹੈ। ਇਨ੍ਹਾਂ ਤਿੰਨਾਂ ਅੰਕਾਂ ਜਾਂ ਜੋੜਾਂ ਵਿੱਚੋਂ, ਕੋਈ ਵੀ ਅੰਕ ਵਰਤਣ ਦੀ ਖੁੱਲ੍ਹ ਹੈ। ਭਾਵੇਂ ਉਨ੍ਹਾਂ ਦੀ ਮਾਣਤਾ ਸੀਮਤ ਜਿਹੀ ਹੀ ਹੈ। ਕੋਈ ਚੰਦ ਦੀ ਸਥਿਤੀ ਦੱਸਣ ਲਈ, ਇਹ ਨਹੀਂ ਕਹਿ ਸਕਦਾ ਕਿ ਉਹ (Piccadilly) ਪਿਕਾਡਿਲੀ ਸਰਕਸ ਤੋਂ ਉੱਤਰ ਜਾਂ ਪੱਛਮ ਵੱਲ ਕਿਤਨੇ ਅੰਕ ਹੈ ਅਤੇ ਸਾਗਰ-ਤੱਟ ਤੋਂ ਕਿਤਨੇ ਫੁੱਟ ਉੱਚਾ ਹੈ। ਇਸ ਦੇ ਉਲਟ, ਕੋਈ ਇਹ ਦੱਸ ਸਕਦਾ ਹੈ, ਕਿ ਚੰਦ ਸੂਰਜ ਤੋਂ ਕਿਤਨੀ ਦੂਰ ਹੈ, ਦੂਜੇ ਗ੍ਰਹਿ ਦੇ ਘੇਰੇ ਤੋਂ ਕਿਤਨੀ ਦੂਰ ਹੈ ਅਤੇ ਚੰਦ ਅਤੇ ਸੂਰਜ ਵਿਚਾਲੇ ਕਿਤਨੀ ਡਿਗਰੀ ਦਾ ਕੋਣ ਹੈ ਅਤੇ (Alpha Centuri) ਅਲਫਾ ਸਟਾਓਰੀ ਵਰਗੇ ਤਾਰੇ ਦੇ ਪੰਧ ਵਿਚਲੀ ਕਿਤਨੀ ਡਿਗਰੀ ਦਾ ਕੋਣ ਹੈ! ਇਹ ਅੰਕ ਵੀ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਸੂਰਜ ਦੀ ਸਥਿਤੀ ਜਾਂ ਇਸ ਬ੍ਰਹਿਮੰਡ ਦੀ ਸਮੁੱਚੀ ਸ੍ਰਿਸ਼ਟੀ ਵਿੱਚ ਸਥਿਤੀ ਦੱਸਣ ਦੇ ਕੰਮ ਨਹੀਂ ਆ ਸਕਦੇ। ਸਮੁੱਚੀ ਸ੍ਰਿਸ਼ਟੀ ਦੀ ਵਿਆਖਿਆ ਕਰਨ ਲਈ ਇਕ-ਦੂਜੇ ਵਿੱਚ ਰਲੇ ਮਿਲੇ ਟੁਕੜਿਆਂ ਦੇ ਸਮੂਹ ਵੱਲੋਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਹਰ ਇਕ (ਟੁਕੜੇ) ਵਿੱਚ ਕਿਸੇ ਬਿੰਦੂ ਦੀ ਸਥਿਤੀ ਦੱਸਣ ਲਈ ਤਿੰਨ ਵੱਖਰੇ-ਵੱਖਰੇ ਅੰਕਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।

ਕੋਈ ਵੀ ਘਟਨਾ ਪੁਲਾੜ ਦੇ ਇਕ ਵਿਸ਼ੇਸ਼ ਬਿੰਦੂ ਉੱਤੇ ਅਤੇ ਕਿਸੇ ਖ਼ਾਸ ਸਮੇਂ ਵਾਪਰਦੀ ਹੁੰਦੀ ਹੈ। ਉਸ ਦੀ ਵਿਆਖਿਆ ਚਾਰ ਅੰਕਾਂ ਜਾਂ ਜੋੜਾਂ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਫੇਰ ਜੋੜਾਂ ਦੀ ਚੋਣ ਆਪਣੀ ਮਰਜ਼ੀ ਅਨੁਸਾਰ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਕੋਈ ਪੁਲਾੜ ਦੇ ਕੋਈ ਵੀ ਤਿੰਨ ਸਪੱਸ਼ਟ ਹੋ ਚੁੱਕੇ ਜੋੜਾਂ ਦੀ ਵਰਤੋਂ ਕਰ ਸਕਦਾ ਹੈ ਅਤੇ ਕੋਈ ਵੀ ਪੈਮਾਨਾ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਵਿੱਚ ਸਮੇਂ ਅਤੇ ਪੁਲਾੜ ਦੇ ਜੋੜਾਂ ਵਿੱਚ ਕੋਈ ਅੰਤਰ ਨਹੀਂ ਦੱਸਿਆ ਗਿਆ ਜਿਵੇਂ ਪੁਲਾੜ ਦੇ ਕਿਸੇ ਵੀ ਦੋ ਜੋੜਾਂ ਵਿੱਚ ਕੋਈ ਫ਼ਰਕ ਨਹੀਂ ਹੋਇਆ ਕਰਦਾ। ਕੋਈ ਜੋੜਾਂ ਦੇ ਕਿਸੇ ਵੀ ਸਮੂਹ ਦੀ ਚੋਣ ਕਰ ਸਕਦਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਮੰਨ ਲਓ, ਕਿ ਪੁਲਾੜ ਦਾ ਪਹਿਲਾ ਜੋੜ, ਪੁਲਾੜ ਦੇ ਪਹਿਲੇ ਅਤੇ ਦੂਜੇ ਜੋੜਾਂ ਦਾ ਮਿਸ਼ਰਣ ਮੰਨਿਆ ਜਾਂਦਾ ਸੀ। ਉਦਾਹਰਣ ਵਜੋਂ ਪਿਕਾਡਿੱਲੀ ਦੇ ਉੱਤਰ ਵਿਚਲੇ ਅਤੇ ਇਸ ਦੇ ਪੱਛਮ ਵੱਲ ਧਰਤੀ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ਨੂੰ ਮੀਲਾਂ ਵਿੱਚ ਨਾਪਣ ਦੀ ਥਾਂ, ਪਿਕਾਡਿਲੀ ਦੇ ਉੱਤਰ ਅਤੇ ਪਿਕਾਡਿਲੀ ਦੇ ਉੱਤਰ-ਪੱਛਮੀ ਦਿਸ਼ਾ ਵਿੱਚ ਮੀਲਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਇਸੇ ਪ੍ਰਕਾਰ ਅਨੁਪਾਤ ਵਿੱਚ ਵੀ ਸਮੇਂ ਦਾ ਕੋਈ ਵੀ ਨਵਾਂ ਜੋੜ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਹੜੇ ਬੀਤੇ ਸਮੇਂ ਵਿੱਚ ਪ੍ਰਾਚੀਨ (ਸਕਿੰਟਾਂ ਵਾਲਾ) ਸਮਾਂ ਹੁੰਦਾ ਸੀ, ਇਸ ਦੇ ਨਾਲ-ਨਾਲ ਪਿਕਾਡਿਲੀ ਦੇ ਉੱਤਰ ਵੱਲ ਦੇ ਫ਼ਾਸਲੇ ਨੂੰ (ਰੌਸ਼ਨੀ ਦੇ ਸਕਿੰਟਾਂ ਵਾਲੇ) ਨੂੰ ਵੀ ਵਰਤ ਸਕਦਾ ਹੈ। ਕਈ ਵਾਰ, ਚਾਰ-ਦਿਸ਼ੀ ਪੁਲਾੜ ਵਿੱਚ, ਜਿਸ ਨੂੰ ਪੁਲਾੜ-ਸਮਾਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ। ਕਿਸੇ ਘਟਨਾ ਵਾਪਰਨ ਦੇ ਬਿੰਦੂ ਦੀ ਵਿਆਖਿਆ ਕਰਨ ਵੇਲੇ ਇਸ ਦੇ ਚਾਰ ਜੋੜਾਂ ਨੂੰ ਵਿਚਾਰਨ ਨਾਲ ਸਹਾਇਤਾ ਮਿਲ ਜਾਂਦੀ ਹੈ। ਚਾਰ-ਦਿਸ਼ੀ ਪੁਲਾੜ ਦੀ ਕਲਪਨਾ ਕਰਨੀ ਸੰਭਵ ਨਹੀਂ ਹੈ। ਪਰੰਤੂ, ਧਰਤੀ ਦੀ ਸਤਾਹ ਵਰਗੇ ਦੋ-ਦਿਸ਼ੀ ਪੁਲਾੜਾਂ ਦੇ ਖ਼ਾਕੇ ਉਲੀਕੇ ਜਾ ਸਕਦੇ ਹਨ। (ਧਰਤੀ ਦੀ ਸਤਾਹ ਦੋ-ਦਿਸ਼ੀ ਹੈ, ਕਿਉਂਕਿ ਕਿਸੇ ਬਿੰਦੂ ਦੀ ਸਥਿਤੀ ਨੂੰ ਦੋ ਜੋੜਾਂ, ਅਰਥਾਤ ਲੈਟੀਚਿਊਡ ਅਤੇ ਲੌਂਗੀਚਿਊਡ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਨਿਸ਼ਚਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।) ਮੈਂ ਸਾਧਾਰਣ ਤੌਰ ‘ਤੇ ਅਜਿਹੇ ਖ਼ਾਕੇ ਉਲੀਕਾਂਗਾ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਸਮਾਂ ਉੱਪਰ ਨੂੰ ਵੱਧਦਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਪੁਲਾੜ ਦੀਆਂ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚੋਂ ਇਕ ਦਿਸ਼ਾ ਨੂੰ ਧਰਤੀ ਦੇ ਬਰਾਬਰ-ਬਰਾਬਰ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਪੁਲਾੜ ਦੀਆਂ ਦੂਜੀਆਂ ਦੋ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚੋਂ ਇਕ ਦਿਸ਼ਾ ਨੂੰ ਧਰਤੀ ਦੇ ਬਰਾਬਰ-ਬਰਾਬਰ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਪੁਲਾੜ ਦੀਆਂ ਦੂਜੀਆਂ ਦੋ ਦਿਸ਼ਾਵਾਂ ਨੂੰ ਨਜ਼ਰ-ਅੰਦਾਜ਼ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ, ਜਾਂ ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇਕ ਨੂੰ Perspective ਵਜੋਂ ਦਿਖਾਇਆ ਜਾਂਦਾ ਹੈ। ਇਨ੍ਹਾਂ ਨੂੰ ਪੁਲਾੜ- ਸਮਾਂ ਖ਼ਾਕੇ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਜਿਵੇਂ ਖ਼ਾਕਾ ਨੰ: 2.1)। ਉਦਾਹਰਣ ਵਜੋਂ ਖ਼ਾਕਾ ਨੰ: 2.2

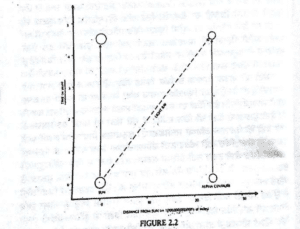
ਵਿੱਚ, ਸਮਾਂ ਉੱਪਰ ਨੂੰ ਨਾਪਿਆ ਗਿਆ ਸਾਲਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਅਤੇ ਸੂਰਜ ਤੋਂ ਅਲਫਾ Alpha Centuari ਤੱਕ ਦੇ ਫ਼ਾਸਲੇ ਨੂੰ ਧਰਤੀ ਦੇ ਨਾਲ-ਨਾਲ ਮੀਲਾਂ ਵਿੱਚ ਨਾਪਿਆ ਗਿਆ ਹੈ। ਸੂਰਜ ਅਤੇ ਅਲਫਾ ਸੰਤੋਰੀ ਦੇ ਰਸਤਿਆਂ ਨੂੰ ਪੁਲਾੜ-ਸਮੇਂ ਵਿਚੀਂ, ਹੇਠਾਂ ਤੋਂ ਉੱਪਰ ਨੂੰ ਖਿੱਚੀਆਂ ਲਾਈਨਾਂ ਨਾਲ ਵਿਖਾਇਆ ਗਿਆ ਹੈ, ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਖ਼ਾਕੇ ਦੇ ਖੱਬੇ ਪਾਸੇ ਹੈ ਅਤੇ ਦੂਜੀ ਸੱਜੇ ਪਾਸੇ ਹੈ। ਸੂਰਜ ਦੀ ਕਿਰਨ ਇਕ ਟੇਢੀ ਲਾਈਨ ਦੇ ਨਾਲ- ਨਾਲ ਚੱਲਦੀ ਹੈ ਅਤੇ ਉਸ ਨੂੰ ਸੂਰਜ ਤੋਂ ਅਲਫਾ ਸੰਤੋਰੀ ਤੱਕ ਪਹੁੰਚਣ ਵਿੱਚ ਚਾਰ ਸਾਲ ਲੱਗਦੇ ਹਨ:

ਜਿਹਾ ਕਿ ਅਸੀਂ ਦੇਖ ਚੁੱਕੇ ਹਾਂ ਕਿ ਮੈਕਸਵੈਲ ਦੀਆਂ ਮੁਸਾਵੀਆਂ ਤੋਂ ਪਤਾ ਲੱਗ ਗਿਆ ਸੀ ਕਿ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਇਕੋ ਰਹਿੰਦੀ ਹੈ, ਭਾਵੇਂ ਰੌਸ਼ਨੀ ਕਿਸੇ ਵੀ ਸੋਮੇ ਤੋਂ ਆਈ ਹੋਵੇ ਅਤੇ ਮਿਣਤੀਆਂ ਕਰਕੇ ਇਸ ਗੱਲ ਦੀ ਸਹੀ-ਸਹੀ ਪੁਸ਼ਟੀ ਹੋ ਚੁੱਕੀ ਹੈ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਜੇ ਰੌਸ਼ਨੀ ਦੀ ਕਿਰਨ ਪੁਲਾੜ ਦੇ ਕਿਸੇ ਖ਼ਾਸ ਬਿੰਦੂ ਉੱਤ ਅਤੇ ਕਿਸੇ ਖ਼ਾਸ ਸਮੇਂ ਨਿਕਲੀ ਹੋਵੇ, ਤਾਂ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਰੌਸ਼ਨੀ ਦੀ ਕਿਰਨ ਚਲ ਕੇ, ਜਿਸ ਦੇ ਆਕਾਰ ਅਤੇ ਸਥਿਤੀ ਦਾ ਕਿਰਨ ਦੇ ਸੋਮੇਂ ਨਾਲ ਕੋਈ ਸੰਬੰਧ ਨਹੀਂ ਹੋਵੇਗਾ। ਇਕ ਸਕਿੰਟ ਦੇ ਦਸ ਲਖਵੇਂ ਹਿੱਸੇ ਵਿੱਚ ਰੌਸ਼ਨੀ ਇਕ ਗੋਲੇ ਦਾ ਰੂਪ ਧਾਰ ਚੁੱਕੀ ਹੋਵੇਗੀ, ਜਿਸ ਦਾ ਘੇਰਾ ਬਿੰਦੂ ਤੋਂ 300 ਮੀਟਰ ਦੂਰ ਹੋਵੇਗਾ ਅਤੇ ਵੀਹ ਲਖਵੇਂ ਸਕਿੰਟ ਵਿੱਚ ਇਹ ਦੂਰੀ ਬਿੰਦੂ ਤੋਂ 600 ਮੀਟਰ ਹੈ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਵੱਧਦੀ ਜਾਵੇਗੀ। ਇਹ ਉਨ੍ਹਾਂ ਲਹਿਰਾਂ ਵਾਂਗ ਹੋਵੇਗਾ, ਜੋ ਟੋਭੇ ਵਿੱਚ, ਪੱਥਰ ਸੁੱਟਣ ਨਾਲ ਪਾਣੀ ਦੀ ਸਤਾਹ ਉੱਤੇ ਲਹਿਰਾਂ ਫੈਲ ਜਾਇਆ ਕਰਦੀਆਂ ਹਨ। ਇਹ ਲਹਿਰਾਂ ਗੋਲ ਘੇਰੇ ਵਿੱਚ ਫੈਲਦੀਆਂ ਹਨ ਅਤੇ ਘੇਰਾ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਵੱਡਾ ਹੁੰਦਾ ਜਾਂਦਾ ਹੈ। ਜੇ ਕੋਈ ਟੋਭੇ ਦੀ ਦੋ-ਦਿਸ਼ੀ ਸਤਾਹ ਦੇ ਤਿੰਨ-ਦਿਸ਼ੀ ਖ਼ਾਕੇ ਨੂੰ ਵਿਚਾਰਨ ਲੱਗੇ ਅਤੇ ਉਸ ਦੇ ਨਾਲ-ਨਾਲ ਇਕ ਦਿਸ਼ੀ ਸਮੇਂ ਨੂੰ ਵੀ ਦੇਖੇ, ਤਾਂ ਲਹਿਰਾਂ ਦਾ ਵੱਧ ਰਿਹਾ ਘੇਰਾ ਇਕ ਤਿਕੋਨ ਦਾ ਰੂਪ ਧਾਰ ਲਵੇਗਾ ਜਿਸ ਦੀ ਨੁੱਕਰ ਉਸ ਥਾਂ ਅਤੇ ਉਸ ਸਮੇਂ ਉੱਤੇ ਸਥਿਤ ਹੋਵੇਗੀ। ਜਿੱਥੇ ਪਾਣੀ ਵਿੱਚ ਪੱਥਰ ਦਾ ਰੋੜਾ ਸੁੱਟਿਆ ਗਿਆ ਸੀ। (ਦੇਖੋ ਚਿੱਤਰ 2.3)। ਇਸੇ ਤਰ੍ਹਾਂ ਰੌਸ਼ਨੀ ਜੋ ਘਟਨਾ ਸਥਾਨ ਤੋਂ

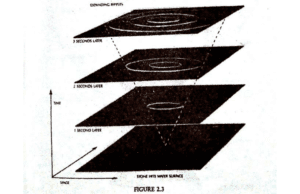
ਫੈਲਣ ਵੇਲੇ ਚਾਰ ਦਿਸ਼ੀ ਸਥਾਨ/ਸਮਾਂ ਵਿੱਚ, ਇਕ ਤਿੰਨ ਦਿਸ਼ੀ ਕੋਣ ਬਣਾ ਲੈਂਦੀ ਹੈ। ਇਸ ਕੋਣ ਨੂੰ ਵਾਪਰਨ ਵਾਲੀ ਘਟਨਾ ਦੀ ਕੋਣ ਕਹਿੰਦੇ ਹਨ। ਇਸੇ ਤਰ੍ਹਾਂ ਅਸੀਂ ਇੱਕ ਹੋਰ ਕੋਣ ਉਲੀਕ ਸਕਦੇ ਹਾਂ, ਜਿਸ ਨੂੰ ਆ ਚੁੱਕੀ ਰੌਸ਼ਨੀ-ਕੋਣ ਕਹਿੰਦੇ ਹਨ, ਜਿਹੜਾ ਕਿ ਘਟਨਾਵਾਂ ਦਾ ਉਹ ਸਮੂਹ ਹੈ, ਜਿੱਥੋਂ ਚੱਲ ਕੇ ਰੌਸ਼ਨੀ ਦੀ ਕਿਰਨ ਘਟਨਾ ਸਥਾਨ ‘ਤੇ ਪਹੁੰਚ ਸਕਦੀ ਹੈ। (ਦੇਖੋ ਖਾਕਾ 2.4)।

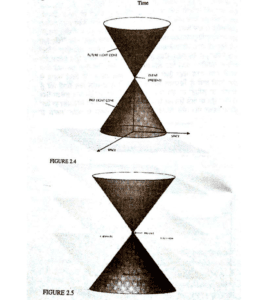
ਘਟਨਾ ਦੀਆਂ ਆ ਚੁੱਕੀਆਂ ਅਤੇ ਆਉਣ ਵਾਲੀਆਂ ਰੌਸ਼ਨੀ-ਕੋਣਾਂ, ਸਥਾਨ, ਸਮੇਂ ਨੂੰ ਤਿੰਨ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡ ਦਿੰਦੀਆਂ ਹਨ। (ਦੇਖੋ ਖ਼ਾਕਾ 2.5)। ਆਉਣ ਵਾਲੀ ਘਟਨਾ ਦਾ ਭਵਿੱਖ ਆਉਣ ਵਾਲੀ P ਨਾਮੀ ਰੌਸ਼ਨੀ-ਕੋਣ ਵਾਲੇ ਹਿੱਸੇ ਵਿੱਚ ਹੁੰਦੀ ਹੈ। ਇਹ ਸਾਰੀਆਂ ਘਟਨਾਵਾਂ ਦਾ ਉਹ ਸਮੂਹ ਹੈ, ਜਿਸ ਉੱਤੇ ‘P’ ਬਿੰਦੂ ਉੱਤੇ ਵਾਪਰਨ ਵਾਲੀਆਂ ਘਟਨਾਵਾਂ ਦਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ। ਜੇ ਕਿਸੇ ਨੂੰ ਇਹ ਪਤਾ ਲੱਗ ਜਾਵੇ, ਪੁਲਾੜ ਦੇ ਖਿੱਤੇ ਵਿਚਲੇ ਹਰ ਇੱਕ ਥਾਂ, ਕਿਸੇ ਖ਼ਾਸ ਸਮੇਂ ਕੀ ਵਾਪਰ ਰਿਹਾ ਹੈ, ਜਿਹੜਾ ਖਿੱਤਾ ‘p’ ਦੇ ਬੀਤ ਚੁੱਕੇ ਰੌਸ਼ਨੀ-ਕੋਣ ਵਿੱਚ ਸਥਿਤ ਹੋਵੇ, ਤਾਂ ਉਸ ਵਿਅਕਤੀ ਨੂੰ ਇਹ ਵੀ ਗਿਆਨ ਹੋ ਜਾਵੇਗਾ ਕਿ ‘P’ ਬਿੰਦੂ ਉੱਤੇ ਕੀ ਵਾਪਰ ਰਿਹਾ ਹੈ। ਪੁਲਾੜ ਦੇ ਖਿੱਤੇ ਵਿਚਲੇ ਹੋਰ ਸਾਰੇ ਸਥਾਨ ਉਹ ਹੁੰਦੇ ਹਨ, ਜਿਹੜੇ ‘P’ ਬਿੰਦੂ ਦੇ ਬੀਤ ਚੁੱਕੇ ਜਾਂ ਆਉਣ ਵਾਲੇ ਰੌਸ਼ਨ ਕੋਣਾਂ ਵਿੱਚ ਸਥਿਤ ਨਹੀਂ ਹੋਇਆ ਕਰਦੇ। ਹੋਰ ਸਥਾਨਾਂ ਉੱਤੇ ਵਾਪਰਨ ਵਾਲੀਆਂ ਘਟਨਾਵਾਂ ਦਾ ‘P’ ਉੱਤੇ ਵਾਪਰਨ ਵਾਲੀਆਂ ਘਟਨਾਵਾਂ ਉੱਤੇ ਕੋਈ ਅਸਰ ਨਹੀਂ ਪੈਂਦਾ।

ਉਦਾਹਰਣ ਵਜੋਂ, ਜੇ ਸੂਰਜ ਇਸੇ ਵੇਲੇ ਚਮਕਣੋਂ ਰੁਕ ਜਾਵੇ, ਉਸ ਦਾ ਇਸੇ ਵੇਲੇ ਧਰਤੀ ਉਤਲੀਆਂ ਵਸਤਾਂ ਉੱਤੇ ਕੋਈ ਅਸਰ ਨਹੀਂ ਪਵੇਗਾ, ਕਿਉਂਕਿ ਉਹ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਵੇਲੇ ਪੁਲਾੜ ਦੇ ਹੋਰ ਸਥਾਨਾਂ ਉੱਤੇ ਸਥਿਤ ਹੋਣਗੀਆਂ। (ਖ਼ਾਕਾ 2.6) ਦੇਖੋ। ਇਸ

 

ਘਟਨਾ ਦਾ ਸਾਨੂੰ ਪਤਾ 8 ਮਿੰਟਾਂ ਮਗਰੋਂ ਲੱਗੇਗਾ, ਜਿਹੜਾ ਸਮਾਂ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਨੂੰ ਧਰਤੀ ਉੱਤੇ ਪਹੁੰਚਣ ਲਈ ਲੱਗ ਜਾਂਦਾ ਹੈ। ਕੇਵਲ ਉਸ ਵੇਲੇ ਹੀ ਧਰਤੀ ਉਤਲੀਆਂ ਘਟਨਾਵਾਂ ਰੌਸ਼ਨੀ ਦੀ ਆਉਣ ਵਾਲੀ ਕੋਣ ਵਿੱਚ ਮੰਨੀਆਂਜਾਣਗੀਆਂ, ਜਿੱਥੇ ਸੂਰਜ ਬੁਝ ਗਿਆ ਸੀ। ਇਸੇ ਪ੍ਰਕਾਰ, ਸਾਨੂੰ ਇਹ ਪਤਾ ਨਹੀਂ ਹੈ ਕਿ ਧਰਤੀ ਉੱਤੇ ਹੋਰ ਦੂਰ ਦੁਰਾਡੇ ਕੀ ਕੁਝ ਵਾਪਰ ਰਿਹਾ ਹੈ ? ਜਿਹੜੀ ਰੌਸ਼ਨੀ ਦੂਜੇ ਗ੍ਰਹਿਆਂ ਵੱਲੋਂ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਉਹ ਲੱਖਾਂ ਵਰ੍ਹੇ ਪਹਿਲਾਂ ਤੋਂ ਚੱਲੀ ਹੋਈ ਹੈ ਅਤੇ ਜਿਹੜਾ ਸਭ ਤੋਂ ਦੁਰਾਡਾ ਗ੍ਰਹਿ ਅਸੀਂ ਹੁਣੇ ਦੇਖਿਆ ਹੈ, ਉਸ ਦੀ ਰੌਸ਼ਨੀ ਨੂੰ ਚੱਲਿਆਂ ਕੋਈ 8 ਖਰਬ ਸਾਲ (ਅੱਠ ਹਜ਼ਾਰ ਮਿਲੀਅਨ ਸਾਲ) ਹੋ ਚੁੱਕੇ ਹਨ। ਇਸ ਤਰ੍ਹਾਂ ਜਿਹੜੀ ਧਰਤੀ ਅਸੀਂ ਦੇਖ ਰਹੇ ਹਾਂ, ਉਸ ਦਾ ਬੀਤ ਚੁੱਕੇ ਸਮੇਂ ਵਾਲਾ ਰੂਪ ਹੈ।

ਜੇ ਕੋਈ ਚੁੰਭਕ ਸ਼ਕਤੀ ਦਾ ਧਿਆਨ ਨਾ ਰੱਖੇ, ਜਿਹਾ ਕਿ ਆਈਨ ਸਟਾਈਨ ਅਤੇ Poincare ਨੇ 1905 ਈਸਵੀ ਵਿੱਚ ਕੀਤਾ ਸੀ, ਤਾਂ ਉਸ ਨੂੰ ਇਸ ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਦਾ ਅਨੁਭਵ ਹੋਵੇਗਾ। ਸਥਾਨੀ ਸਮੇਂ ਦੀ ਤਰ੍ਹਾਂ ਇਕ ਘਟਨਾ ਲਈ ਸਾਨੂੰ ਇਕ ਰੌਸ਼ਨੀ ਕੋਣ ਉਲੀਕਣੀ ਪਵੇਗੀ। ਉਸ ਵੇਲੇ ਹੀ ਤਾਂ ਸਥਾਨ/ਸਮੇਂ ਵਿਚਲੀ ਰੌਸ਼ਨੀ ਦੇ ਸਾਰੇ ਹੀ ਸੰਭਵ ਰਸਤੇ ਉਭਰੇ ਸਨ। ਅਤੇ ਹਰ ਇਕ ਘਟਨਾ ਵੇਲੇ ਅਤੇ ਹਰ ਪਾਸੇ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਇਕੋ ਜਿਹੀ ਹੋਇਆ ਕਰਦੀ ਹੈ। ਇਸ ਲਈ ਰੌਸ਼ਨੀ ਦੀਆਂ ਸਭ ਕੋਣਾਂ ਇਕੋ ਜਿਹੀਆਂ ਹੋਣਗੀਆਂ ਅਤੇ ਸਾਰੀਆਂ ਦੀ ਦਿਸ਼ਾ ਵੀ ਇਕੋ ਹੋਵੇਗੀ। ਸਿਧਾਂਤ ਤਾਂ ਸਾਨੂੰ ਇਹੋ ਦੱਸਦਾ ਹੈ ਕਿ ਕੋਈ ਚੀਜ਼ ਵੀ ਰੌਸ਼ਨੀ ਨਾਲੋਂ ਤੇਜ਼ ਰਫ਼ਤਾਰ ਨਹੀਂ ਹੋ ਸਕਦੀ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੋਇਆ ਕਿ ਸਥਾਨ ਅਤੇ ਸਮੇਂ ਦੇ ਘੇਰੇ ਵਿੱਚ ਆਉਣ ਵਾਲੀ ਹਰ ਇਕ ਵਸਤੂ ਦੇ ਰਸਤੇ ਦਾ ਪ੍ਰਗਟਾਅ ਉਹ ਲਕੀਰ ਕਰੇਗੀ ਜਿਹੜੀ ਹਰ ਇਕ ਘਟਨਾ ਨਾਲ ਸੰਬੰਧ ਰੱਖਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਕੋਣ ਵਿੱਚ ਖਿੱਚੀ ਜਾਵੇਗੀ (ਦੇਖੋ ਖ਼ਾਕਾ 2.7)।

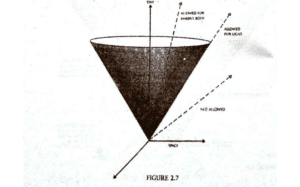
ਅਨੁਪਾਤ ਦੇ ਵਿਸ਼ੇਸ਼ ਸਿਧਾਂਤ ਨੂੰ ਇਹ ਗੱਲ ਦੱਸਣ ਵਿੱਚ ਬਹੁਤ ਸਫ਼ਲਤਾ ਮਿਲੀ ਕਿ ਸਾਰੇ ਦਰਸ਼ਕਾਂ ਨੂੰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਇਕੋ ਪ੍ਰਤੀਤ ਹੋਵੇਗੀ (ਜਿਹਾ ਕਿ ਮਿਚਲਸਨ ਮੌਰਲੀ ਦੇ ਤਜਰਬੇ ਨੇ ਸਿੱਧ ਕਰ ਦਿੱਤਾ ਸੀ) ਅਤੇ ਇਹ ਵੀ ਦੱਸ ਦਿੱਤਾ ਸੀ ਕਿ ਉਸ ਵੇਲੇ ਕੀ ਕੁਝ ਵਾਪਰਦਾ ਹੈ। ਜਦੋਂ ਵਸਤਾਂ ਦੀ ਰਫ਼ਤਾਰ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਦੇ ਨੇੜੇ- ਤੇੜੇ ਹੋ ਜਾਂਦੀ ਹੈ। ਪਰੰਤੂ ਇਹ ਸਿਧਾਂਤ ਨਿਊਟਨ ਦੇ ਖਿੱਚ ਵਾਲੇ ਸਿਧਾਂਤ ਨਾਲ ਮੇਲ ਨਹੀਂ ਖਾਂਦਾ, ਜਿਸ ਅਨੁਸਾਰ ਸਾਰੀਆਂ ਵਸਤੂਆਂ ਉਨ੍ਹਾਂ ਵਿਚਲੇ ਫ਼ਾਸਲੇ ਦੇ ਹਿਸਾਬ ਨਾਲ, ਇਕ ਦੂਜੀ ਵੱਲ ਖਿੱਚੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੋਇਆ ਕਿ ਜੇ ਕੋਈ ਕਿਸੇ ਵੀ ਵਸਤੂ ਨੂੰ ਚਲਾ ਦੇਵੇ, ਤਾਂ ਦੂਜੀ ਵਸਤੂ ਦੀ ਸ਼ਕਤੀ ਫੌਰਨ ਹੀ ਬਦਲ ਜਾਂਦੀ ਹੈ। ਜਾਂ ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਖਿੱਚ-ਪਾਊ ਪ੍ਰਭਾਵ ਅਥਾਹ ਸ਼ਕਤੀ (ਰਫ਼ਤਾਰ) ਨਾਲ ਚੱਲਣੇ ਚਾਹੀਦੇ ਹਨ, ਨਾ ਕਿ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਦੇ ਬਰਾਬਰ ਜਾਂ ਉਸ ਤੋਂ ਘੱਟ ਰਫ਼ਤਾਰ ਨਾਲ। ਜਿਹਾ ਕਿ ਅਨੁਪਾਤ ਦੇ ਵਿਸ਼ੇਸ਼ ਸਿਧਾਂਤ ਅਨੁਸਾਰ ਹੁੰਦਾ ਹੈ। ਨਿਊਟਨ ਨੇ 1908 ਅਤੇ 1914 ਵਿਚਕਾਰ ਜਾਣਨ ਲਈ ਕਿ ਖਿੱਚ ਵਾਲਾ ਸਿਧਾਂਤ ਅਨੁਪਾਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਨਾਲ ਮਿਲਦਾ-ਜੁਲਦਾ ਹੋਵੇ, ਕਈ ਨਾਕਾਮ ਕੋਸ਼ਿਸ਼ਾਂ ਕੀਤੀਆਂ ਸਨ। ਆਖ਼ਰ 1915 ਵਿੱਚ ਉਸ ਨੇ ਉਹ ਸਿਧਾਂਤ ਪੇਸ਼ ਕਰ ਦਿੱਤਾ ਸੀ, ਜਿਸ ਨੂੰ ਅਸੀਂ ਅਨੁਪਾਤ ਦਾ ਵਿਸ਼ੇਸ਼ ਸਿਧਾਂਤ ਕਹਿੰਦੇ ਹਾਂ।

ਆਈਨਸਟਾਈਨ ਨੇ ਇਕ ਜੁਗ-ਪਲਟਾਊ ਸੁਝਾਉ ਦਿੱਤਾ ਕਿ ਖਿੱਚ ਦੂਜੀਆਂ ਸ਼ਕਤੀਆਂ ਵਰਗੀ ਸ਼ਕਤੀ ਨਹੀਂ ਹੈ, ਸਗੋਂ ਇਹ ਤਾਂ ਇਸ ਗੱਲ ਦਾ ਸਿੱਟਾ ਹੈ ਕਿ ਸਥਾਨੀ ਸਮਾਂ ਚਪਟਾ ਨਹੀਂ ਹੈ, ਜਿਵੇਂ ਕਿ ਪਹਿਲਾਂ ਮੰਨਿਆ ਜਾਂਦਾ ਸੀ। ਇਹ ਤਾਂ ਮੁੜਿਆ ਹੋਇਆ, ਜਾਂ ਟੇਢਾ ਮੇਢਾ ਹੈ ਅਤੇ ਇਸ ਦਾ ਕਾਰਨ ਇਸ ਵਿਚਲੀਆਂ ਸ਼ਕਤੀਆਂ ਅਤੇ

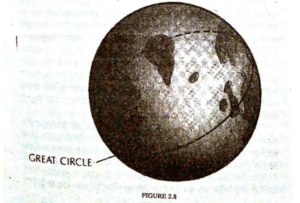
ਆਕਾਰ ਸਦਕਾ ਪਈਆਂ ਹੋਈਆਂ ਵੰਡੀਆਂ ਹਨ। ਧਰਤੀ ਵਰਗੀਆਂ ਪਦਾਰਥਕ ਵਸਤੂਆਂ ਖਿੱਚ ਰੂਪੀ ਸ਼ਕਤੀ ਸਦਕਾ ਟੇਢੇ ਘੇਰੇ (ਚੱਕਰ) ਲਾਉਣ ਵਾਲੀਆਂ ਨਹੀਂ ਹਨ, ਇਸ ਦੇ ਉਲਟ, ਉਹ ਤਾਂ ਟੇਢੇ ਪੁਲਾੜ ਵਿਚਲੀ ਸੜਕ ਦੇ ਨੇੜਲੀ ਵਸਤੂ ਦੇ ਪਿੱਛੇ-ਪਿੱਛੇ ਤੁਰਦੀਆਂ ਹਨ, ਜਿਸ ਨੂੰ Geodesic (ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਦੋ ਟੇਢੀਆਂ ਵਸਤਾਂ ਵਿਚਕਾਰ ਲਕੀਰ) ਕਹਿੰਦੇ ਹਨ। ਇਹ ਦੋ ਬਿੰਦੂਆਂ ਵਿਚਕਾਰਲੀ ਛੋਟੀ ਤੋਂ ਛੋਟੀ (ਜਾਂ ਲੰਮੀ) ਲਕੀਰ ਹੁੰਦੀ ਹੈ। ਉਦਾਹਰਣ ਵਜੋਂ, ਧਰਤੀ ਦੀ ਸਤਾਹ ਦੋ-ਦਿਸ਼ੀ ਟੇਢਾ ਪੁਲਾੜ ਹੈ। ਧਰਤੀ ਉੱਤੇ ਇਸ ਲਕੀਰ ਨੂੰ ਇਕ ਵੱਡਾ ਗੋਲ ਚੱਕਰ ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਇਹ ਦੋ ਬਿੰਦੂਆਂ ਵਿਚਾਲੇ ਛੋਟੇ ਤੋਂ ਛੋਟਾ ਫ਼ਾਸਲਾ ਹੈ । (ਦੇਖੋ ਖ਼ਾਕਾ 2.8)। ਦੋ ਹਵਾਈ ਅੱਡਿਆਂ ਦੇ ਵਿਚਾਲੇ ਇਹ ਛੋਟੇ ਤੋਂ ਛੋਟਾ ਰਸਤਾ ਹੁੰਦਾ ਹੈ, (ਇਸ ਲਈ ਜਹਾਜ਼ਾਂ ਦਾ ਮਾਹਿਰ ਚਾਲਕ ਇਸ ਰਸਤੇ ਜਹਾਜ਼ ਚਲਾਉਣ ਲਈ ਕਹੇਗਾ। ਆਮ ਅਨੁਪਾਤ ਵਿੱਚ, ਵਸਤਾਂ ਚਾਰ-ਦਿਸ਼ੀ ਸਥਾਨ/ ਸਮੇਂ ਵਿਚਲੀਆਂ ਸਿੱਧੀਆਂ ਲਕੀਰਾਂ ਉੱਤੇ ਚੱਲਦੀਆਂ ਹਨ, ਪਰੰਤੂ ਸਾਨੂੰ ਐਉਂ ਜਾਪਦਾ ਹੈ ਕਿ ਉਹ ਸਾਡੇ ਤਿੰਨ-ਦਿਸ਼ੀ ਪੁਲਾੜ ਦੇ ਵਿੰਗੇ ਟੇਢੇ ਰਸਤਿਆਂ ਉੱਤੇ ਚੱਲਦੀਆਂ ਹਨ। ਇਹ ਤਾਂ ਪਰਬਤੀ ਧਰਤੀ ਉੱਤੇ ਉੱਡਣ ਵਾਲੇ ਹਵਾਈ ਜਹਾਜ਼ ਨੂੰ ਦੇਖਣ ਵਾਲੀ ਗੱਲ ਹੈ। ਭਾਵੇਂ ਇਹ ਤਿੰਨ-ਦਿਸ਼ੀ ਪੁਲਾੜ ਵਿਚਲੀ ਸਿੱਧੀ ਲਕੀਰ ਤੇ ਉੱਡਦਾ ਹੁੰਦਾ ਹੈ, ਇਸ ਦਾ ਪਰਛਾਵਾਂ, ਦੋ-ਦਿਸ਼ੀ ਧਰਤੀ ਉੱਤੇ ਟੇਢੇ ਰਸਤੇ ਉੱਤੇ ਪੈਂਦਾ ਹੈ। ਸੂਰਜ ਦਾ ਆਕਾਰ ਸਥਾਨ/ਸਮੇਂ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਟੇਢੀ ਕਰ ਦਿੰਦਾ ਹੈ ਕਿ ਭਾਵੇਂ ਧਰਤੀ ਚਾਰ ਦਿਸ਼ੀ ਪੁਲਾੜ ਵਿੱਚ ਇਕ ਸਿੱਧੀ ਲਕੀਰ ‘ਤੇ ਚਲਦੀ ਹੈ, ਪਰ ਜਾਪਦੀ ਐਉਂ ਹੈ, ਜਿਵੇਂ ਤਿੰਨ ਦਿਸ਼ੀ ਪੁਲਾੜ ਵਿੱਚ, ਇਹ ਗੋਲ ਚੱਕਰ ਲਾਉਂਦੀ ਹੋਵੇ। ਅਸਲ ਵਿੱਚ, ਅਨੁਪਾਤ ਦੇ ਸਿਧਾਂਤ ਵੱਲੋਂ ਦੱਸੇ ਸਾਂਝੇ ਗ੍ਰਹਿਆਂ ਦੇ ਗੋਲ ਚੱਕਰ ਐਨ ਉਨ੍ਹਾਂ ਚੱਕਰਾਂ ਵਰਗੇ ਹੀ ਹਨ, ਜਿਹੜੇ ਨਿਊਟਨ ਦਾ ਖਿੱਚ ਵਾਲਾ ਸਿਧਾਂਤ ਪ੍ਰਗਟਾਉਂਦਾ ਹੈ। ਪਰੰਤੂ ਸੂਰਜ ਦੇ ਸਭ ਤੋਂ ਨੇੜਲੇ ਮਰਕਰੀ ਗ੍ਰਹਿ ਉੱਤੇ ਖਿੱਚ ਦੇ ਸਭ ਤੋਂ ਵੱਧ ਜ਼ਬਰਦਸਤ ਅਸਰ ਪੈਂਦੇ ਹਨ ਅਤੇ ਇਸ ਦਾ ਚੱਕਰ ਵਿੰਗਾ ਟੇਢਾ ਹੈ, ਅਨੁਪਾਤ ਦਾ ਆਮ ਸਿਧਾਂਤ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਕਿ ਇਸ ਗ੍ਰਹਿ ਦਾ ਲੰਮਾ ਧੁਰਾ, ਸੂਰਜ ਦੁਆਲੇ ਦਸ ਹਜ਼ਾਰ ਸਾਲ ਵਿੱਚ ਇਕ ਡਿਗਰੀ ਦੇ ਹਿਸਾਬ ਨਾਲ ਘੁੰਮਣਾ ਚਾਹੀਦਾ ਹੈ। ਇਹ ਅਸਰ ਭਾਵੇਂ ਅਤਿ ਮਾਮੂਲੀ ਜਿਹਾ ਹੈ। ਇਸ ਦਾ ਅਨੁਭਵ 1915 ਈਸਵੀ ਵਿੱਚ ਹੋ ਗਿਆ ਸੀ ਅਤੇ ਇਹ ਆਈਨ ਸਟਾਈਨ ਦੇ ਸਿਧਾਂਤ ਦੀਆਂ ਪੁਸ਼ਟੀਆਂ ਵਿੱਚੋਂ ਇਕ ਸੀ। ਹੁਣੇ-ਹੁਣੇ ਬੀਤੇ ਸਾਲਾਂ ਵਿੱਚ, ਨਿਊਟਨ ਦੇ ਸਿਧਾਂਤ ਅਨੁਸਾਰ, ਦੂਜੇ ਗ੍ਰਹਿਆਂ ਦੇ ਚੱਕਰਾਂ ਵਿਚਲੇ ਇਸ ਤੋਂ ਛੋਟੇ ਅਸਰਾਂ ਨੂੰ ਜਦੋਂ ਰਾਡਾਰ ਸਦਕਾ ਮਿਣਿਆ ਗਿਆ, ਤਾਂ ਉਹ ਵੀ ਅਨੁਪਾਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਵੱਲੋਂ ਦਰਸਾਏ ਨਤੀਜਿਆਂ ਨਾਲ ਮੇਲ ਖਾਂਦੇ ਪਾਏ ਗਏ।

ਰੌਸ਼ਨੀ ਦੀਆਂ ਕਿਰਨਾਂ ਨੂੰ ਵੀ ਸਥਾਨ/ਸਮੇਂ ਵਿਚਲੇ ਛੋਟੇ ਤੋਂ ਛੋਟੇ ਰਸਤੇ ਉੱਤੇ ਸ਼ੱਲਣਾ ਚਾਹੀਦਾ ਹੈ। ਫੇਰ, ਪੁਲਾੜ ਦੇ ਟੇਢ ਦਾ ਅਰਥ ਹੈ ਕਿ ਰੌਸ਼ਨੀ ਪੁਲਾੜ ਦੀਆਂ ਸਿੱਧੀਆਂ ਲਕੀਰਾਂ ਅਨੁਸਾਰ ਸਫ਼ਰ ਨਹੀਂ ਕਰਦੀ। ਇਸ ਲਈ ਅਨੁਪਾਤ ਦਾ ਆਮ ਸਿਧਾਂਤ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਕਿ ਰੌਸ਼ਨੀ ਖਿੱਚ ਪਾਊ ਪਿੜ ਸਦਕਾ ਟੇਢੀ ਹੋ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ। ਉਦਾਹਰਣ ਵਜੋਂ, ਇਹ ਸਿਧਾਂਤ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਕਿ ਸੂਰਜ ਦੇ ਨਜ਼ਦੀਕੀ ਰੌਸ਼ਨੀ ਕੋਣਾਂ ਦੇ ਬਿੰਦੂ ਅੰਦਰ ਵੱਲ ਝੁਕ ਜਾਣੇ ਚਾਹੀਦੇ ਹਨ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਇਕ ਦੁਰਾਡੇ ਤਾਰੇ ਤੋਂ ਆਉਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਵਿੱਚ ਸੂਰਜ ਦੇ ਨੇੜਿਉਂ ਲੰਘਣ ਸਮੇਂ, ਇਕ ਕੋਣ ਬਣ ਜਾਵੇਗਾ ਅਤੇ ਧਰਤੀ ਉਤਲੇ ਦਰਸ਼ਕ ਨੂੰ ਉਸ ਤਾਰੇ ਦੀ ਸਥਿਤੀ ਵੱਖਰੀ ਨਜ਼ਰ ਆਵੇਗੀ (ਦੇਖੋ ਖਾਕਾ 29)।

ਹਾਂ ਜੇ ਤਾਰੇ ਤੋਂ ਆਉਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਨੂੰ ਸੂਰਜ ਦੇ ਨੇੜਿਉਂ ਲੰਘਣਾ ਹੀ ਪੈਂਦਾ. ਹੈ, ਤਾਂ ਅਸੀਂ ਇਹ ਨਹੀਂ ਦੱਸ ਸਕਾਂਗੇ ਕਿ ਰੌਸ਼ਨੀ ਨੂੰ ਟੇਢਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ; ਜਾਂ ਨਹੀਂ। ਜਾਂ ਇਸ ਦੇ ਉਲਟ, ਇਹ ਕਿ ਤਾਰਾ ਸੱਚੀ-ਮੁੱਚੀ ਉਸੇ ਥਾਂ ਹੈ, ਜਿੱਥੇ ਸਾਨੂੰ ਨਜ਼ਰ ਆ ਰਿਹਾ ਹੈ। ਪਰੰਤੂ, ਕਿਉਂਕਿ ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮ ਰਹੀ ਹੈਂ, ਭਿੰਨ-ਭਿੰਨ ਤਾਰੇ ਸੂਰਜ ਦੇ ਪਰਲੇ ਪਾਸਿਉਂ ਲੰਘਦੇ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਰੌਸ਼ਨੀ ਸਾਵੀਂ ਨਹੀਂ ਰਹਿੰਦੀ। ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਦੀ ਜ਼ਾਹਰੀ ਸਥਿਤੀ ਦੂਜੇ ਤਾਰਿਆਂ ਪ੍ਰਤੀ ਬਦਲ ਜਾਂਦੀ ਹੈ। ਅਜਿਹਾ ਪ੍ਰਭਾਵ ਦੇਖਣਾ ਬਹੁਤ ਕਠਿਨ ਹੈ, ਕਿਉਂਕਿ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਵਿੱਚ ਉਹ ਤਾਰੇ ਦੇਖ ਸਕਣਾ ਅਸੰਭਵ ਹੋ ਜਾਂਦਾ ਹੈ, ਜਿਹੜੇ ਆਕਾਸ਼ ਵਿੱਚ ਸੂਰਜ ਦੇ ਨੇੜੇ ਹੁੰਦੇ ਹਨ। ਪਰੰਤੂ ਅਜਿਹੇ ਤਾਰੇ ਸੂਰਜ ਗ੍ਰਹਿਣ ਸਮੇਂ ਦੇਖ ਸਕਣਾ ਸੰਭਵ ਹੈ, ਜਦੋਂ ਚੰਦ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਨੂੰ ਰੋਕ ਲੈਂਦਾ ਹੈ। 1915 ਈਸਵੀ ਵਿੱਚ, ਆਈਨ ਸਟਾਈਨ ਵੱਲੋਂ ਦਰਸਾਈ ਗਈ ਰੌਸ਼ਨੀ ਦੇ ਟੇਢੇਪਣ ਦੀ ਪਰਖ ਨਹੀਂ ਸੀ ਹੋ ਸਕਦੀ ਕਿਉਂਕਿ ਪਹਿਲਾ ਵਿਸ਼ਵ ਯੁੱਧ ਚੱਲ ਰਿਹਾ ਸੀ, ਅਤੇ 1919 ਈਸਵੀ ਤੱਕ ਵੀ ਨਹੀਂ ਸੀ ਪਰਖੀ ਜਾ ਸਕੀ ਸੀ, ਜਦੋਂ ਤੱਕ ਪੱਛਮੀ ਅਫ਼ਰੀਕਾ ਵਿੱਚ, ਇਕ ਫਰੰਗੀਆਂ ਦੀ ਟੋਲੀ ਨੇ ਗ੍ਰਹਿਣ ਸਮੇਂ ਇਹ ਜ਼ਾਹਰ ਕੀਤਾ ਸੀ ਕਿ ਰੌਸ਼ਨੀ ਸੱਚੀਮੁੱਚੀ ਟੇਢੀ ਹੋ ਜਾਂਦੀ ਹੈ ਜੋ ਕਿ ਸਿਧਾਂਤ ਦੀ ਖੋਜ ਦੇ ਅਨੁਸਾਰ ਸੀ। ਜਰਮਨਾਂ ਦੇ ਅਜਿਹੇ ਸਿਧਾਂਤ ਦਾ ਸਬੂਤ, ਬਰਤਾਨਵੀ ਵਿਗਿਆਨੀਆਂ ਨੇ ਬਹੁਤ ਪਸੰਦ ਕੀਤਾ ਸੀ ਅਤੇ ਇਸ ਨੂੰ ਯੁੱਧ ਸਮਾਪਤ ਹੋਣ ਉਪਰੰਤ ਦੋਹਾਂ ਦੇਸ਼ਾਂ ਦੇ ਸਹਿਯੋਗ ਨੂੰ ਬਹੁਤ ਸ਼ਲਾਘਾਯੋਗ ਮੰਨਿਆ ਸੀ। ਮੰਦ-ਭਾਗੀ ਗੱਲ ਤਾਂ ਇਹ ਹੈ ਕਿ ਉਸ ਮੁਹਿੰਮ ਦੀਆਂ ਮੂਰਤਾਂ ਦੀ ਪਛੜ ਕੇ ਕੀਤੀ ਪੜਤਾਲ ਤੋਂ ਪਤਾ ਲੱਗਿਆ ਸੀ ਕਿ ਪ੍ਰਾਪਤ ਕੀਤੇ ਸਿੱਟਿਆਂ ਵਿੱਚ ਬਹੁਤ ਗੰਭੀਰ ਭੁੱਲਾਂ ਸਨ। ਉਨ੍ਹਾਂ ਵੱਲੋਂ ਕੀਤੀ ਮਿਣਤੀ, ਇਕ ਨਿਰੋਲ ਕਿਸਮਤ ਵਾਲੀ ਗੱਲ ਸੀ ਅਤੇ ਪਹਿਲੇ ਸਿੱਟੇ ਨੂੰ ਜਾਣਨ ਤੱਕ ਸੀਮਿਤ ਸੀ ਅਤੇ ਵਿਗਿਆਨ ਦੇ ਖੇਤਰ ਵਿੱਚ ਇਹ ਕੋਈ ਅਦਭੁੱਤ ਪ੍ਰਾਪਤੀ ਨਹੀਂ ਸੀ। ਪਰੰਤੂ ਰੌਸ਼ਨੀ ਦੇ ਟੇਢੇਪਣ ਨੂੰ ਅੱਗੇ ਜਾ ਕੇ ਕਈ ਦਰਸ਼ਕਾਂ ਨੇ ਬਿਲਕੁਲ ਸਹੀ-ਸਹੀ ਨਾਪ ਲਿਆ ਸੀ।

ਅਨੁਪਾਤ ਦੇ ਸਾਧਾਰਣ ਸਿਧਾਂਤ ਤੋਂ ਇਕ ਹੋਰ ਗਿਆਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ਕਿ ਧਰਤੀ ਵਰਗੇ ਬਹੁ-ਆਕਾਰੀ ਗ੍ਰਹਿ ਦੇ ਨੇੜੇ ਸਮੇਂ ਦੀ ਰਫ਼ਤਾਰ ਮਠੇਰੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ। ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਰੌਸ਼ਨੀ ਦੀ ਸ਼ਕਤੀ ਅਤੇ ਇਸ ਦੇ ਵਾਰ-ਵਾਰ ਆਉਣ ਦੀ ਗਤੀ ਵਿਚਕਾਰ ਇਕ ਸੰਬੰਧ ਹੈ (ਅਰਥਾਤ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਦੀ ਇਕ ਸਕਿੰਟ ਪ੍ਰਤੀ ਮਿਣਤੀ) ਜਿਤਨੀ ਵੱਧ ਸ਼ਕਤੀ ਹੋਵੇਗੀ, ਉਤਨੀ ਹੀ ਲਹਿਰਾਂ ਦੀ ਗਤੀ ਵੱਧ ਹੋਵੇਗੀ। ਜਦੋਂ ਰੌਸ਼ਨੀ ਧਰਤੀ ਦੇ ਖਿੱਚ-ਪਾਊ ਪਿੜ ਵਿੱਚ, ਉੱਪਰ ਨੂੰ ਜਾਂਦੀ ਹੈ, ਇਸ ਦੀ ਸ਼ਕਤੀ ਘੱਟ ਜਾਂਦੀ ਹੈ ਅਤੇ ਨਾਲ ਦੀ ਨਾਲ ਇਸ ਦੀ ਗਤੀ ਵੀ ਘੱਟ ਜਾਂਦੀ ਹੈ।

(ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੋਇਆ ਕਿ ਲਹਿਰਾਂ ਵਿਚਲੇ ਸਮੇਂ ਵਿੱਚ ਵਾਧਾ ਹੋ ਜਾਂਦਾ ਹੈ।) ਉੱਚਾਈ ਉੱਤੇ ਬੈਠੇ ਵਿਅਕਤੀ ਨੂੰ ਐਉਂ ਜਾਪੇਗਾ ਕਿ ਹੇਠਾਂ ਘਨਟਾਵਾਂ ਨੂੰ ਵਾਪਰਨ ਵਿੱਚ ਵਧੇਰੇ ਸਮਾਂ ਲੱਗਦਾ ਹੈ, ਜਾਂ ਉਹ ਹੌਲੀ-ਹੌਲੀ ਹੀ ਵਾਪਰ ਰਹੀਆਂ ਹਨ। ਇਸ ਪ੍ਰਾਪਤੀ ਦੀ ਪਰਖ, 1962 ਵਿੱਚ, ਇਕ ਪਾਣੀ ਦੀ ਟੈਂਕੀ ਦੇ ਸਿਖਰ ਅਤੇ ਉਸ ਦੇ ਥੱਲੇ ਦੋ ਸਹੀ ਹਾਲਤ ਵਾਲੇ ਕਲਾਕ ਵਰਤ ਕੇ ਕੀਤੀ ਗਈ ਸੀ। ਹੇਠਲਾ ਕਲਾਕ ਜੋ ਧਰਤੀ ਦੇ ਨੇੜੇ ਸੀ, ਹੌਲੀ-ਹੌਲੀ ਚੱਲਦਾ ਪ੍ਰਤੀਤ ਹੋਇਆ, ਜੋ ਅਨੁਪਾਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਨਾਲ ਮੇਲ ਖਾਂਦਾ ਸੀ। ਧਰਤੀ ਤੋਂ ਭਿੰਨ-ਭਿੰਨ ਕਲਾਕਾਂ ਦੀ ਰਫ਼ਤਾਰ ਦਾ ਅੰਤਰ ਅੱਜ ਕੱਲ੍ਹ ਅਮਲੀ ਤੌਰ ਤੇ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਹੈ, ਜਦੋਂ ਕਿ ਸੈਟਲਾਈਟਾਂ ਤੋਂ ਮਿਲੇ ਇਸ਼ਾਰਿਆਂ ਅਨੁਸਾਰ, ਸਮੁੰਦਰੀ ਜਹਾਜ਼ ਸਹੀ ਢੰਗ ਨਾਲ ਚੱਲਣ ਲੱਗ ਪਏ ਹਨ। ਜੇ ਕੋਈ ਅਨੁਪਾਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਦਾ ਧਿਆਨ ਨਾ ਰੱਖੇ, ਤਾਂ ਉਸ ਦੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਸਥਿਤੀ ਵਿੱਚ ਕਈ ਮੀਲਾਂ ਦੀ ਗ਼ਲਤੀ ਹੋ ਜਾਵੇਗੀ।

ਨਿਊਟਨ ਦੇ ਗਤੀ ਵਾਲੇ ਨਿਯਮਾਂ ਨਾਲ ਪੁਲਾੜ ਵਿੱਚ ਨਿਸ਼ਚਿਤ ਸ਼ਕਤੀ ਦੇ ਵਿਚਾਰ ਦਾ ਅੰਤ ਹੋ ਜਾਂਦਾ ਹੈ। ਅਨੁਪਾਤ ਦਾ ਸਿਧਾਂਤ ਪੱਕੇ ਸਮੇਂ ਦੇ ਵਿਚਾਰ ਤੋਂ ਸ਼ਕਤੀ ਪਾਉਂਦਾ ਹੈ। ਦੋ ਜੋੜਿਆਂ ਨੂੰ ਵਿਚਾਰ ਕੇ ਦੇਖੋ। ਫ਼ਰਜ਼ ਕਰ ਲਓ ਕਿ ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇਕ ਪਰਬਤ ਦੀ ਟੀਸੀ ਉੱਤੇ ਰਹਿਣ ਲੱਗ ਜਾਂਦਾ ਹੈ ਅਤੇ ਦੂਜਾ ਸਾਗਰ ਦੀ ਪੱਧਰ ਉੱਤੇ ਹੀ ਟਿਕ ਗਿਆ ਹੈ। ਪਹਿਲੇ ਦੀ ਉਮਰ ਵਿੱਚ, ਦੂਜੇ ਦੀ ਉਮਰ ਨਾਲੋਂ ਛੇਤੀ ਵਾਧਾ ਹੋ ਜਾਵੇਗਾ। ਇਸ ਤਰ੍ਹਾਂ ਜਦੋਂ ਉਹ ਦੋਬਾਰਾ ਮਿਲਣਗੇ, ਤਾਂ ਪਹਿਲਾ ਦੂਜੇ ਨਾਲੋਂ ਉਮਰ ਵਿੱਚ ਵੱਡਾ ਹੋ ਜਾਵੇਗਾ। ਇਸ ਹਾਲਤ ਵਿੱਚ, ਉਨ੍ਹਾਂ ਦੀ ਉਮਰ ਵਿਚਲਾ ਅੰਤਰ ਮਾਮੂਲੀ ਹੋਵੇਗਾ, ਪਰੰਤੂ ਜੇ ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇਕ ਪੁਲਾੜ ਜਹਾਜ਼ ਵਿੱਚ, ਜੋ ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਦੇ ਨੇੜੇ-ਤੇੜੇ ਉੱਡਦਾ ਹੋਵੇ, ਲੰਮੇ ਸਮੇਂ ਲਈ ਚਲਿਆ ਜਾਵੇ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੀ ਉਮਰ ਵਿਚਲਾ ਅੰਤਰ ਬਹੁਤ ਲੰਮਾ ਹੋ ਜਾਵੇਗਾ। ਜਦੋਂ ਉਹ ਵਾਪਸ ਪਰਤੇਗਾ, ਉਹ ਹੇਠਾਂ ਰਹਿਣ ਵਾਲੇ ਨਾਲੋਂ ਉਮਰ ਵਿੱਚ ਛੋਟਾ ਪ੍ਰਤੀਤ ਹੋਵੇਗਾ। ਇਸ ਨੂੰ ਜੋੜਿਆਂ ਦਾ ਅਚੰਭਾ ਕਹਿੰਦੇ ਹਨ। ਪਰੰਤੂ ਇਹ ਅਚੰਭਾ ਤਾਂ ਅਨੁਭਵ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ ਕਿਸੇ ਦੇ ਮਨ ਵਿੱਚ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਦਾ ਵਿਚਾਰ ਮੌਜੂਦ ਹੋਵੇ। ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਵਿੱਚ, ਕੋਈ ਨਿਸ਼ਚਿਤ ਸਮਾਂ ਨਹੀਂ ਮੰਨਿਆ ਜਾਂਦਾ, ਪਰੰਤੂ ਇਸ ਦੇ ਉਲਟ, ਹਰ ਇਕ ਵਿਅਕਤੀ ਲਈ ਆਪਣਾ-ਆਪਣਾ ਸਮਾਂ ਹੋਇਆ ਕਰਦਾ ਹੈ, ਇਸ ਗੱਲ ਦੇ ਆਧਾਰ ‘ਤੇ ਕਿ ਉਹ ਕਿੱਥੇ ਹੈ ਅਤੇ ਉਹ ਕਿਵੇਂ ਚੱਲ ਰਿਹਾ ਹੈ?

1915 ਤੋਂ ਪਹਿਲਾਂ, ਸਥਾਨ ਅਤੇ ਸਮੇਂ ਨੂੰ ਇਕ ਜਕੜਿਆ ਹੋਇਆ ਅਖਾੜਾ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ, ਜਿਸ ਵਿੱਚ ਘਟਨਾਵਾਂ ਵਾਪਰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਸਨ, ਪਰੰਤੂ ਇਨ੍ਹਾਂ ਘਟਨਾਵਾਂ ਦਾ ਉਸ ਅਖਾੜੇ ਉੱਤੇ ਕੋਈ ਅਸਰ ਨਹੀਂ ਸੀ ਹੁੰਦਾ। ਇਹ ਗੱਲ ਅਨੁਪਾਤ ਦੇ ਖ਼ਾਸ ਸਿਧਾਂਤ ਅਨੁਸਾਰ ਵੀ ਸੱਚੀ ਮੰਨੀ ਜਾਂਦੀ ਸੀ । ਵਸਤੂਆਂ ਚਲਦੀਆਂ ਫਿਰਦੀਆਂ, ਸ਼ਕਤੀਆਂ ਨੂੰ ਖਿੱਚ ਪੈਂਦੀ ਰਹਿੰਦੀ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਰੁਕਾਵਟਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ, ਫੇਰ ਵੀ ਸਮਾਂ ਅਤੇ ਸਥਾਨ ਜਾਰੀ ਰਹਿੰਦੇ ਅਤੇ ਉਨ੍ਹਾਂ ਉੱਤੇ ਕਿਸੇ ਪ੍ਰਕਾਰ ਦਾ ਅਸਰ ਨਹੀਂ ਸੀ ਪਿਆ ਕਰਦਾ। ਇਹ ਸੋਚਣਾ ਸੁਭਾਵਿਕ ਹੀ ਸੀ ਕਿ ਸਥਾਨ ਅਤੇ ਸਮਾਂ ਸਦਾ ਹੀ ਚੱਲਦੇ ਅਤੇ ਜਾਰੀ ਰਹਿੰਦੇ ਸਨ।

ਪਰੰਤੂ, ਅਨੁਪਾਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਵਿੱਚ ਸਥਿਤੀ ਉੱਕਾ ਹੀ ਵੱਖਰੀ ਹੈ। ਅੱਜ ਕੱਲ੍ਹ ਸਥਾਨ ਅਤੇ ਸਮਾਂ ਹਰ ਸਮੇਂ ਬਦਲਦੇ ਰਹਿਣ ਵਾਲੇ ਮੰਨੇ ਜਾਂਦੇ ਹਨ। ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਹਰਕਤ ਵਿੱਚ ਆਉਂਦੀ ਹੈ ਜਾਂ ਕੋਈ ਕਾਰਜ-ਸ਼ੀਲ ਹੋ ਜਾਂਦੀ ਹੈ, ਸਥਾਨ ਅਤੇ ਸਮੇਂ ਵਿੱਚ ਫੈੜ ਪੈ ਜਾਂਦੇ ਹਨ। ਇਸ ਦੇ ਨਾਲ-ਨਾਲ, ਸਥਾਨ/ਸਮਾਂ ਉਨ੍ਹਾਂ ਵਸਤੂਆਂ ਦੀ ਹਰਕਤ ਨੂੰ ਅਤੇ ਸ਼ਕਤੀ ਦੀ ਕਾਰਜ-ਕੁਸ਼ਲਤਾ ਉੱਤੇ ਅਸਰ-ਅੰਦਾਜ਼ ਹੋ ਜਾਂਦੇ ਹਨ। ਸਥਾਨ ਅਤੇ ਸਮਾਂ ਹੀ ਕੇਵਲ ਅਸਰ-ਅੰਦਾਜ਼ ਨਹੀਂ ਹੁੰਦੇ ਸਗੋਂ ਧਰਤੀ ਉੱਤੇ ਵਾਪਰਨ ਵਾਲੀ ਹਰ ਇਕ ਘਟਨਾ ਦਾ ਉਨ੍ਹਾਂ ਉੱਤੇ ਵੀ ਅਸਰ ਪੈਂਦਾ ਹੈ। ਜਿਵੇਂ ਕੋਈ ਇਹ ਨਹੀਂ ਕਹਿ ਸਕਦਾ ਕਿ ਧਰਤੀ ਦੀਆਂ ਘਟਨਾਵਾਂ ਸਥਾਨ/ਸਮੇਂ ਦੀ ਹਰਕਤ ਤੋਂ ਬਿਨਾਂ ਹੀ ਵਾਪਰ ਰਹੀਆਂ ਹਨ, ਇਸ ਲਈ, ਅਨੁਪਾਤ ਦੇ ਖ਼ਾਸ ਸਿਧਾਂਤ ਅਨੁਸਾਰ ਇਹ ਕਹਿਣਾ ਵਿਅਰਥ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿ ਸਥਾਨ ਅਤੇ ਸਮਾਂ ਧਰਤੀ ਦੀਆਂ ਹੱਦਾਂ ਤੋਂ ਬਾਹਰ ਹਨ।

ਆਉਣ ਵਾਲੇ ਦਹਾਕਿਆਂ ਵਿੱਚ, ਸਥਾਨ ਅਤੇ ਸਮੇਂ ਬਾਰੇ ਇਸ ਸੋਚ ਸਦਕਾ ਧਰਤੀ ਬਾਰੇ ਸਾਡੇ ਵਿਚਾਰਾਂ ਵਿੱਚ ਪਰਿਵਰਤਨ ਲਿਆਉਣਾ ਸੀ। ਪੁਰਾਣਾ ਇਹ ਵਿਚਾਰ ਕਿ ਧਰਤੀ ਅਦਲਾ-ਬਦਲੀ ਤੋਂ ਰਹਿਤ, ਜਿਹੜੀ ਪਹਿਲਾਂ ਤੋਂ ਹੀ ਮੌਜੂਦ ਰਹੀ ਹੈ ਅਤੇ ਅੱਗੋਂ ਲਈ ਵੀ ਮੌਜੂਦ ਰਹੇਗੀ, ਬਦਲ ਗਿਆ ਅਤੇ ਇਸ ਦੀ ਥਾਂ ਇਸ ਵਿਚਾਰ ਨੇ ਮੱਲ ਲਈ ਕਿ ਧਰਤੀ ਗਤੀਸ਼ੀਲ ਹੈ, ਇਹ ਫੈਲ ਰਹੀ ਹੈ ਅਤੇ ਇਸ ਦਾ ਅਰੰਭ ਕੁਝ ਸਮਾਂ ਪਹਿਲਾਂ, ਇਕ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਹੋਇਆ ਹੈ ਅਤੇ ਇਹ ਕਿ ਭਵਿੱਖ ਵਿੱਚ ਕਿਸੇ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਇਸ ਦਾ ਅੰਤ ਵੀ ਹੋ ਸਕਦਾ ਹੈ। ਅਜਿਹਾ ਪਰਿਵਰਤਨ ਅਗਲੇ ਕਾਂਡ ਦਾ ਵਿਸ਼ਾ ਹੈ ਅਤੇ ਕਈ ਸਾਲਾਂ ਮਗਰੋਂ, ਮੇਰੇ ਵੱਲੋਂ ਸਿਧਾਂਤਕ ਫਿਜ਼ਿਕਸ ਦਾ ਕਾਰਜ ਵੀ ਇਸੇ ਸਮੇਂ ਤੋਂ ਸ਼ੁਰੂ ਹੋਵੇਗਾ। ਰੋਜਰ ਪੈਨਰੋਜ (Roger Pencrose) ਅਤੇ ਮੈਂ ਇਹ ਪ੍ਰਗਟ ਕਰ ਚੁੱਕੇ ਹਾਂ ਕਿ ਆਈਨਸਟਾਈਨ ਦੇ ਅਨੁਪਾਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਤੋਂ ਐਉਂ ਪ੍ਰਤੀਤ ਹੁੰਦਾ ਹੈ ਕਿ ਧਰਤੀ ਦਾ ਮੁੱਢ ਵੀ ਕਿਸੇ ਸਮੇਂ ਬੱਝਿਆ ਹੋਵੇਗਾ ਅਤੇ ਇਸ ਦੇ ਅੰਤ ਦੀ ਸੰਭਾਵਨਾ ਵੀ ਹੈ।

ਫੈਲ ਰਹੀ ਧਰਤੀ

ਜੇ ਕੋਈ ਸਾਫ਼ ਅਤੇ ਨ੍ਹੇਰੀ ਰਾਤ ਨੂੰ ਆਕਾਸ਼ ਵੱਲ ਤੱਕੇ ਤਾਂ ਉਹ ਸਭ ਤੋਂ ਵੱਧ ਚਮਕਦਾਰ ਗ੍ਰਹਿ ਵੀਨਸ, ਮਾਰੀਸ਼, ਜੁਪੀਟਰ ਅਤੇ ਸੈਚਰਨ ਦੇਖੇਗਾ। ਆਕਾਸ਼ ਵਿੱਚ ਹੋਰ ਵੀ ਬਹੁਤ ਸਾਰੇ ਤਾਰੇ ਨਜ਼ਰ ਆਉਣਗੇ; ਜਿਹੜੇ ਸਾਡੇ ਸੂਰਜ ਵਰਗੇ ਹੀ ਹਨ, ਪਰ ਸਾਥੋਂ ਬਹੁਤ ਹੀ ਦੂਰ ਹਨ। ਇਨ੍ਹਾਂ ਵਿੱਚ ਕੁੱਝ ਜੋ ਅਚਲ ਤਾਰੇ ਹਨ, ਉਹ ਆਪਣੇ ਅਸਥਾਨ ਬਦਲਦੇ ਪ੍ਰਤੀਤ ਹੁੰਦੇ ਹਨ ਜਦੋਂ ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਚੱਕਰ ਕੱਟਦੀ ਹੈ, ਪਰ ਉੱਨਾ ਦੀ ਆਪਸੀ ਸਥਿਤੀ ਵਿੱਚ ਬਹੁਤ ਅਮੂਲੀ ਤਬਦੀਲੀ ਹੁੰਦੀ ਹੈ। ਅਸਲ ਵਿੱਚ ਉਹ ਬਿਲਕੁਲ ਅਚੱਲ ਤਾਰੇ ਨਹੀਂ ਹਨ। ਉਕਤ ਤਬਦੀਲੀ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਉਹ ਦੂਜਿਆਂ ਨਾਲੋਂ ਸਾਡੇ ਕੁਝ ਨੇੜੇ ਹਨ। ਜਦੋਂ ਧਰਤੀ ਘੁੰਮ ਰਹੀ ਹੁੰਦੀ ਹੈ, ਅਸੀਂ ਉਨ੍ਹਾਂ ਤਾਰਿਆਂ ਨੂੰ ਬਹੁਤ ਦੁਰਾਡੇ ਤਾਰਿਆਂ ਦੀ ਪਛੋਕੜ ਭਿੰਨ-ਭਿੰਨ ਥਾਂਵਾਂ ਤੋਂ ਦੇਖ ਰਹੇ ਹੁੰਦੇ ਹਾਂ। ਇਹ ਖ਼ੁਸ਼ ਕਿਸਮਤੀ ਵਾਲੀ ਗੱਲ ਹੈ ਕਿਉਂਕਿ ਇਸੇ ਕਾਰਨ ਕਰਕੇ ਅਸੀਂ ਤਾਰਿਆਂ ਦੀ ਸਾਥੋਂ ਦੂਰੀ ਨੂੰ ਸਿੱਧੇ ਤੌਰ ‘ਤੇ ਨਾਪਣ ਦੇ ਯੋਗ ਹੋ ਜਾਂਦੇ ਹਾਂ, ਉਹ ਜਿਤਨੇ ਨੇੜੇ ਹੁੰਦੇ ਹਨ, ਉਹ ਚੱਲ ਰਹੇ ਪ੍ਰਤੀਤ ਹੁੰਦੇ ਹਨ। ਸਭ ਤੋਂ ਨੇੜਲਾ ਤਾਰਾ, ਪਰੌਕਸੀਆ ਸੰਤੌਰੀ ਹੈ। ਉਹ ਧਰਤੀ ਤੋਂ ਰੌਸ਼ਨੀ ਦੇ ਚਾਰ ਸਾਲਾਂ ਦੀ ਦੂਰੀ ਉੱਤੇ ਹੈ। (ਇਸ ਤੋਂ ਆਉਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਨੂੰ ਧਰਤੀ ਉੱਤੇ ਪਹੁੰਚਣ ਲਈ ਚਾਰ ਸਾਲ ਲੱਗਦੇ ਹਨ) ਜਾਂ ਦੋ ਕਰੋੜ ਤੀਹ ਲੱਖ ਮਿਲੀਅਨ ਮੀਲ ਦੂਰ ਹੈ। ਹੋਰ ਬਹੁਤ ਸਾਰੇ ਤਾਰੇ, ਜੋ ਆਸਾਨੀ ਨਾਲ ਦੇਖੇ ਜਾ ਸਕਦੇ ਹਨ, ਰੌਸ਼ਨੀ ਦੇ ਕੁਝ ਸੈਂਕੜੇ ਸਾਲਾਂ ਦੀ ਦੂਰੀ ਉੱਤੇ ਹਨ। ਸਾਡਾ ਸੂਰਜ, ਟਾਕਰੇ ਵਜੋਂ, ਕੇਵਲ ਰੌਸ਼ਨੀ ਦੇ ਅੱਠ ਮਿੰਟਾਂ ਦੀ ਦੂਰੀ ‘ਤੇ ਹੈ। ਨਜ਼ਰ ਆਉਣ ਵਾਲੇ ਤਾਰੇ ਆਕਾਸ਼ ਵਿੱਚ ਸਾਰੇ ਆਕਾਸ਼ ਵਿੱਚ ਖਿਲਰੇ ਹੋਏ ਪ੍ਰਤੀਤ ਹੁੰਦੇ ਹਨ, ਪਰੰਤੂ ਉਹ ਤਾਂ ਖ਼ਾਸ ਤੌਰ ‘ਤੇ ਇੱਕ ਪੱਟੀ ਵਿੱਚ ਇਕੱਠੇ ਹੀ ਹਨ, ਜਿਸ ਨੂੰ ਅਸੀਂ Milky Way ਕਹਿੰਦੇ ਹਾਂ। 1750 ਈਸਵੀ ਵਿੱਚ ਕੁਝ ਨਜ਼ੂਮੀਂ ਦੱਸਦੇ ਸਨ ਕਿ ਮਿਲਕੀ ਵੇ ਦਾ ਵੇਰਵਾ ਤਾਂ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਜੇ ਨਜ਼ਰ ਆ ਰਹੇ ਤਾਰਿਆਂ ਵਿੱਚੋਂ ਬਹੁਤੇ ਇੱਕੋ ਤਖ਼ਤੀ ਵਿੱਚ ਸਥਿਤ ਹੋਣ, ਜਿਸ ਦੀ ਉਦਾਹਰਣ ਵਜੋਂ ਸਾਡਾ ਅਜੋਕਾ ਪੇਚਦਾਰ ਬਹਿਮੰਡ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ। ਕੁਝ ਹੀ ਦਹਾਕਿਆਂ ਉਪਰੰਤ, ਵਿਲੀਅਮ ਹਰਸ਼ਲ (Sir Wiliam Herschel) ਨਜੂਮੀ ਨੇ ਅਣਥਕ ਮਿਹਨਤ ਕਰਕੇ, ਆਪਣੇ ਵਿਚਾਰ ਦੀ ਪੁਸ਼ਟੀ ਝਹੁਤ ਸਾਰੇ ਤਾਰਿਆਂ ਦੀਆਂ ਸਥਿਤੀਆਂ ਅਤੇ ਦੂਰੀਆਂ ਦੀ ਸੂਚੀ ਤਿਆਰ ਕਰਕੇ ਕੀਤੀ ਸੀ। ਫੇਰ ਵੀ, ਇਸ ਵਿਚਾਰ ਨੂੰ ਚਾਲੂ ਸ਼ਤਾਬਦੀ ਦੇ ਅਰੰਭ ਵਿੱਚ ਹੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੋਈ ਸੀ। ਬ੍ਰਹਿਮੰਡ ਦੀ ਆਧੁਨਿਕ ਤਸਵੀਰ ਦਸੰਬਰ, 1924 ਈ: ਵਿੱਚ ਹੀ ਬਣੀ ਸੀ, ਜਦੋਂ ਅਮਰੀਕਾ ਦੇ ਨਜੂਮੀ ਐਡਵਿਨ ਹੁਬੱਲ (Edwin Humble) ਨੇ ਜਦੋਂ ਇਹ ਸਾਬਤ ਕਰ ਦਿਖਾਇਆ ਸੀ ਕਿ ਕੇਵਲ ਸਾਡਾ ਬ੍ਰਹਿਮੰਡ ਹੀ ਮੌਜੂਦ ਨਹੀਂ ਹੈ। ਅਸਲ ਵਿੱਚ ਹੋਰ ਵੀ ਬ੍ਰਹਿਮੰਡ ਮੌਜੂਦ ਸਨ, ਜਿਨ੍ਹਾਂ ਦੇ ਵਿਚਕਾਰ ਵਿਸ਼ਾਲ ਖ਼ਾਲੀ ਪੁਲਾੜ ਸਨ। ਇਹ ਸਾਬਤ

ਕਰਨ ਲਈ, ਉਸ ਨੂੰ ਇਨ੍ਹਾਂ ਦੂਜੇ ਬ੍ਰਹਿਮੰਡਾਂ ਵਿਚਲੇ ਫ਼ਾਸਲੇ ਨਿਸ਼ਚਿਤ ਕਰਨ ਦੀ ਲੋੜ ਪਈ ਸੀ, ਜਿਹੜੇ ਬਹੁਤ ਹੀ ਦੂਰ-ਦੁਰਾਡੇ ਹਨ, ਤਾਰਿਆਂ ਵਾਂਗੂੰ ਨਹੀਂ, ਉਹ ਸਾਰੇ ਇਕੋ ਥਾਂ ਟਿਕੇ ਹੋਏ ਜਾਪਦੇ ਹਨ। ਇਸ ਲਈ ਹੁਬੱਲ ਨੂੰ ਇਹ ਫ਼ਾਸਲੇ ਲੰਘਣ ਲਈ ਕਈ ਅਸਿੱਧੇ ਢੰਗ ਵਰਤਣੇ ਪਏ ਸਨ। ਹੁਣ ਇਕ ਤਾਰੇ ਦੀ ਚਮਕ ਦੋ ਗੱਲਾਂ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ, ਇਸ ਵਿੱਚੋਂ ਕਿਤਨੀ ਰੌਸ਼ਨੀ ਉਪਜਦੀ ਹੈ ਅਤੇ ਇਹ ਸਾਥੋਂ ਕਿਤਨੀ ਦੂਰੀ ‘ਤੇ ਹੈ। ਨਜ਼ਦੀਕੀ ਤਾਰਿਆਂ ਤੋਂ ਉਨ੍ਹਾਂ ਦੀ ਜ਼ਾਹਰਾ ਚਮਕ ਨੂੰ ਮਿਣ ਸਕਦੇ ਹਾਂ ਅਤੇ ਉਸ ਦੇ ਫ਼ਾਸਲੇ ਨੂੰ ਵੀ ਨਾਪ ਸਕਦੇ ਹਾਂ; ਤਾਂ ਜੋ ਉਨ੍ਹਾਂ ਦੀ ਚਮਕ ਦਾ ਨਿਰਣਾ ਕਰ ਸਕੀਏ। ਇਸ ਦੇ ਉਲਟ, ਜੇ ਸਾਨੂੰ ਦੂਜੇ ਬ੍ਰਹਿਮੰਡਾਂ ਦੇ ਤਾਰਿਆਂ ਦੀ ਰੌਸ਼ਨੀ ਦਾ ਪਤਾ ਹੁੰਦਾ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੀ ਜ਼ਾਹਰਾ ਚਮਕ ਦੇ ਆਧਾਰ ‘ਤੇ ਅਸੀਂ ਉਨ੍ਹਾਂ ਦੇ ਫ਼ਾਸਲੇ ਵੀ ਨਾਪ ਸਕਦੇ ਸੀ। ਹੁਬੱਲ ਨੇ ਦੇਖ ਲਿਆ ਕਿ ਕੁਝ ਤਾਰਿਆਂ ਦੀ ਚਮਕ ਇਕੋ ਜਿਹੀ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ, ਜਦੋਂ ਉਸ ਨੂੰ ਮਿਣਨ ਲਈ ਉਹ ਸਾਡੇ ਨੇੜੇ ਹੋਣ, ਇਸ ਲਈ ਉਸ ਦੀ ਦਲੀਲ ਸੀ ਕਿ ਜੇ ਸਾਨੂੰ ਦੂਜੇ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਇਸੇ ਪ੍ਰਕਾਰ ਦੇ ਤਾਰਿਆਂ ਦਾ ਪਤਾ ਲੱਗ ਜਾਵੇ, ਤਾਂ ਅਸੀਂ ਅਨੁਭਵ ਕਰ ਸਕਦੇ ਹਾਂ ਕਿ ਉਨ੍ਹਾਂ ਦੀ ਚਮਕ ਵੀ ਬਰਾਬਰ ਹੀ ਹੈ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਬ੍ਰਹਿਮੰਡ ਦਾ ਫ਼ਾਸਲਾ ਵੀ ਨਾਪ ਸਕਦੇ ਹਾਂ। ਜੇ ਅਸੀਂ ਉਸੇ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਕਈ ਤਾਰਿਆਂ ਦਾ ਇਸੇ ਪ੍ਰਕਾਰ ਪਤਾ ਲਾ ਸਕੀਏ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਫ਼ਾਸਲੇ ਵੀ ਇਕੋ ਜਿੰਨੇ ਹੋਣ, ਤਾਂ ਸਾਡੇ ਅੰਦਾਜ਼ੇ ਸਹੀ ਹੋਣ ਬਾਰੇ ਸਾਨੂੰ ਵਿਸ਼ਵਾਸ ਹੋ ਸਕਦਾ ਹੈ।

ਇਹ ਢੰਗ ਵਰਤ ਕੇ, ਹੁਬੱਲ ਨੇ ਨੌਂ ਵੱਖਰੇ-ਵੱਖਰੇ ਬ੍ਰਹਿਮੰਡਾਂ ਦੇ ਫ਼ਾਸਲਿਆਂ ਦਾ ਨਿਰਣਾ ਕਰ ਲਿਆ ਸੀ। ਹੁਣ ਸਾਨੂੰ ਪਤਾ ਹੈ ਕਿ ਸਾਡਾ ਬ੍ਰਹਿਮੰਡ ਲੱਖਾਂ ਕਰੋੜਾਂ ਬ੍ਰਹਿਮੰਡਾਂ ਵਿੱਚੋਂ ਇਕ ਹੈ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਆਧੁਨਿਕ ਦੂਰਬੀਨਾਂ ਨਾਲ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਹਰ ਇਕ ਬ੍ਰਹਿਮੰਡ ਵਿੱਚ ਅਰਬਾਂ ਹੀ ਤਾਰੇ ਮੌਜੂਦ ਹਨ। ਖ਼ਾਕਾ ਨੰ. 3.1 ਵਿੱਚ ਇਕ ਪੇਚ-ਦਾਰ ਬ੍ਰਹਿਮੰਡ ਦੀ ਤਸਵੀਰ ਹੈ, ਜਿਹੜਾ ਐਨ ਉਸ ਤਸਵੀਰ ਵਰਗਾ ਜਾਪਦਾ ਹੈ, ਜਿਸ ਪ੍ਰਕਾਰ ਦੀ ਕਿਸੇ ਹੋਰ ਬ੍ਰਹਿਮੰਡ ਤੋਂ ਦੇਖਿਆਂ ਸਾਡੇ ਬ੍ਰਹਿਮੰਡ ਦੀ ਤਸਵੀਰ ਨਜ਼ਰ ਆਏਗੀ। ਅਸੀਂ ਅਜਿਹੇ ਬ੍ਰਹਿਮੰਡ ਦੇ ਵਸਨੀਕ ਹਾਂ, ਜਿਹੜਾ ਰੌਸ਼ਨੀ ਦੇ ਇਕ ਲੱਖ ਸਾਲਾਂ ਜਿਤਨਾ ਵਿਸ਼ਾਲ ਹੈ ਅਤੇ ਹੌਲੀ-ਹੌਲੀ ਘੁੰਮ ਰਿਹਾ ਹੈ ਅਤੇ ਇਸ ਦੀਆਂ ਪੇਚਦਾਰ ਬਾਂਹਾਂ ਵਿਚਲੇ ਤਾਰੇ ਇਸ ਦੇ ਕੇਂਦਰ ਬਿੰਦੂ ਦੁਆਲੇ, ਕਈ ਅਰਬ ਸਾਲਾਂ ਵਿੱਚ, ਕੇਵਲ ਇਕ ਚੱਕਰ ਲਾਉਂਦੇ ਹਨ। ਸਾਡਾ ਸੂਰਜ ਇਕ ਮਾਮੂਲੀ ਔਸਤ ਦਰਜੇ ਦੇ ਆਕਾਰ ਵਾਲਾ ਪੀਲਾ ਤਾਰਾ ਹੈ ਅਤੇ ਪੇਚਦਾਰ ਬਾਂਹਾਂ ਵਿੱਚ ਇਕ ਨੁੱਕਰ ਉੱਤੇ ਸਥਿਤ ਹੈ। ਅਸੀਂ ਅਰਸਤੂ ਅਤੇ ਟੌਮੀ (Ptolemy) ਦੇ ਸਮੇਂ ਤੋਂ ਬਹੁਤ ਅੱਗੇ ਲੰਘ ਚੁੱਕੇ ਹਾਂ, ਜਦੋਂ ਸਾਡਾ ਖ਼ਿਆਲ ਸੀ ਕਿ ਸਾਡੀ ਧਰਤੀ ਬ੍ਰਹਿਮੰਡ ਦਾ ਕੇਂਦਰ ਸੀ।

ਤਾਰੇ ਸਾਥੋਂ ਇਤਨੇ ਦੂਰ ਹਨ ਕਿ ਉਹ ਸਾਨੂੰ ਰੌਸ਼ਨੀ ਦੀਆਂ ਸੂਈਆਂ (ਪਿਨਾਂ) ਦੇ ਸਿਰਿਆਂ ਜਿੰਨੇ ਜਾਪਦੇ ਹਨ। ਅਸੀਂ ਉਨ੍ਹਾਂ ਦਾ ਆਕਾਰ ਜਾਂ ਰੂਪ ਦੇਖ ਨਹੀਂ ਸਕਦੇ। ਫੇਰ ਅਸੀਂ ਵੱਖਰੇ-ਵੱਖਰੇ ਤਾਰਿਆਂ ਦਾ ਵੇਰਵਾ ਕਿਵੇਂ ਦੱਸ ਸਕਦੇ ਹਾਂ ? ਤਾਰਿਆਂ ਦੀ ਬਹੁ- ਗਿਣਤੀ ਵਿੱਚ ਇਕ ਸਾਂਝਾ ਲੱਛਣ ਇਹ ਜ਼ਰੂਰ ਹੈ, ਕਿ ਉਨ੍ਹਾਂ ਦੀ ਰੌਸ਼ਨੀ ਦਾ ਰੰਗ ਇਕੋ ਜਿਹਾ ਹੈ। ਨਿਊਟਨ ਨੇ ਇਹ ਪਤਾ ਕਰ ਲਿਆ ਸੀ ਕਿ ਜੇ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਤਿਕੋਣ ਸ਼ੀਸ਼ੇ ਵਿੱਚੀਂ ਲੰਘੇ ਤਾਂ ਇਹ ਆਪਣੇ ਮਿਲੇ-ਜੁਲੇ ਰੰਗਾਂ ਵਿੱਚ ਖਿੰਡ ਜਾਂਦੀ ਹੈ। ਜਿਵੇਂ ਕਿ ਸਤਰੰਗੀ ਪੀਂਘ ਵੇਲੇ ਹੋਇਆ ਕਰਦਾ ਹੈ। ਕਿਸੇ ਇਕੱਲੇ ਤਾਰੇ ਜਾਂ ਗ੍ਰਹਿ ਵੱਲ ਦੂਰਬੀਨ ਨਾਲ ਤੱਕਿਆ, ਤਾਂ ਦਰਸ਼ਕ ਤਾਰੇ ਜਾਂ ਗ੍ਰਹਿ ਦੀ ਰੌਸ਼ਨੀ ਦੇ ਮਿਸ਼ਰਤ ਰੰਗਾਂ ਨੂੰ ਦੇਖ ਸਕੇਗਾ। ਭਿੰਨ-ਭਿੰਨ ਤਾਰਿਆਂ ਦੇ ਵੱਖਰੇ ਰੰਗ ਹੋਇਆਂ ਕਰਦੇ ਹਨ; ਪਰੰਤੂ ਵੱਖਰੇ-ਵੱਖਰੇ ਰੰਗਾਂ ਦੀ ਅਨੁਪਾਤਕ ਚਮਕ, ਐਨ ਉਸ ਰੰਗ ਵਰਗੀ ਹੀ ਹੋਵੇਗੀ, ਜਿਹੜੀ ਸੁਲਘ ਰਹੀ ਅੱਗ ਵਰਗੀ ਤੱਤੀ ਚਮਕ ਰਹੀ ਜਾਪਦੀ ਹੋਵੇ। (ਅਸਲ ਵਿੱਚ, ਕਿਸੇ Opaque ਵਸਤੂ ਵਿੱਚੋਂ ਆਉਣ ਵਾਲੀ ਅੱਗ ਵਰਗੀ ਗਰਮ ਰੌਸ਼ਨੀ ਵਿੱਚ ਰੰਗਾਂ ਦਾ ਮਿਸ਼ਰਨ ਉਸ ਦੇ ਤਾਪਮਾਨ ਉੱਤੇ ਨਿਰਭਰ ਹੁੰਦਾ ਹੈ—A Thermal Spectrum) ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਅਸੀਂ ਕਿਸੇ ਵੀ ਤਾਰੇ ਦੇ ਤਾਪਮਾਨ ਨੂੰ ਉਸ ਦੀ ਰੌਸ਼ਨੀ ਦੇ ਮਿਸ਼ਰਤ ਰੰਗਾਂ ਨੂੰ ਮੁਖ ਰੱਖ ਕੇ ਨਾਪ ਸਕਦੇ ਹਾਂ। ਪਰੰਤੂ ਕਈ ਵਾਰ ਤਾਰਿਆਂ ਦੇ ਰੰਗਾਂ ਦੇ ਮਿਸ਼ਰਨ ਵਿੱਚੋਂ ਕੁਝ ਵਿਸ਼ੇਸ਼ ਰੰਗ ਗੁਆਚੇ ਮਹਿਸੂਸ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਹ ਗੁਆਚੇ ਹੋਏ ਰੰਗ ਵੱਖਰੇ-ਵੱਖਰੇ ਹੁੰਦੇ ਹਨ। ਕਿਉਂਕਿ ਸਾਨੂੰ ਪਤਾ ਹੈ ਕਿ ਹਰ ਇਕ ਕੈਮੀਕਲ ਤੱਤ, ਖ਼ਾਸ ਮਿਸ਼ਰਤ ਰੰਗਾਂ ਦੇ ਸਮੂਹ ਨੂੰ ਜਜ਼ਬ ਕਰ ਸਕਦਾ ਹੈ, ਅਜਿਹੇ ਰੰਗਾਂ ਦਾ ਗੁਆਚੇ ਰੰਗਾਂ ਨਾਲ ਮਿਲਾਨ ਕਰਕੇ ਅਸੀਂ ਇਹ ਨਿਰਣਾ ਕਰ ਸਕਦੇ ਹਾਂ ਕਿ ਉਸ ਤਾਰੇ ਦੇ ਚੁਗਿਰਦੇ ਵਿੱਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਰੰਗ ਮੌਜੂਦ ਹਨ ? 1920 ਵਿੱਚ, ਜਦੋਂ ਨਜੂਮੀਆਂ ਨੇ ਦੂਜੇ ਗ੍ਰਹਿਆਂ ਦੇ ਤਾਰਿਆਂ ਦੇ ਰੰਗਾਂ ਨਾਲ ਦੇਖਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਸੀ, ਉਨ੍ਹਾਂ ਨੂੰ ਕੁਝ ਅਜਿਹੀ ਚੀਜ਼ ਦਾ ਪਤਾ ਲੱਗਿਆ : ਉਨ੍ਹਾਂ ਤਾਰਿਆਂ ਦੇ ਰੰਗਾਂ ਦਾ ਲੱਛਣ ਸਾਡੇ ਗੁਪਤ ਤਾਰਿਆਂ ਦੇ ਰੰਗਾਂ ਵਰਗਾ ਹੀ ਸੀ; ਪਰੰਤੂ ਉਹ ਵੀ ਉਸੇ ਅਨੁਪਾਤਕ ਮਾਤਰਾ ਵਿੱਚੋਂ ਰੰਗਾਂ ਦੇ ਸਿਰੇ ਵੱਲ ਧੱਕੇ ਜਾਂਦੇ ਸਨ। ਇਸ ਗੁੰਝਲ ਨੂੰ ਸਮਝਣ ਲਈ, ਸਾਨੂੰ ਪਹਿਲਾਂ Doppler Effect ਸਮਝਣਾ ਪਵੇਗਾ। ਜਿਵੇਂ ਅਸੀਂ ਦੇਖ ਚੁੱਕੇ ਹਾਂ ਕਿ ਨਜ਼ਰ ਆਉਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਵਿੱਚ ਹਿਲ-ਜੁਲ ਹੁੰਦੀ ਰਹਿੰਦੀ ਹੈ, ਜਾਂ (ਉਸ ਵਿੱਚ ਸਕਿੰਟ ਪ੍ਰਤੀ ਲਹਿਰਾਂ ਪੈਦਾ ਹੁੰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ)। ਬਹੁਤ ਹੀ ਤੇਜ਼ ਰਫ਼ਤਾਰ ਹੁੰਦੀਆਂ ਹਨ, ਚਾਰ ਤੋਂ ਲੈ ਕੇ ਸੱਤ (Hundred million million per second) ਰੌਸ਼ਨੀ ਦੀਆਂ ਵੱਖਰੀਆਂ ਰਫ਼ਤਾਰਾਂ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਹੜੀਆਂ ਮਨੁੱਖ ਨੂੰ ਵੱਖਰੇ ਰੰਗ ਪ੍ਰਤੀਤ ਹੁੰਦੇ ਹਨ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਰਫ਼ਤਾਰ ਸੱਤ-ਰੰਗੀ ਪੀਪ ਦੇ ਨਾਲ ਸਿਰੇ ਉੱਤੇ ਨਜ਼ਰ ਆਵੇ ਅਤੇ ਸਭ ਤੋਂ ਤੇਜ਼ ਰਫ਼ਤਾਰਾਂ ਨੀਲੇ ਸਿਰੇ ਉੱਤੇ ਹੁੰਦੀਆਂ ਹਨ। ਹੁਣ ਆਪਣੇ ਆਪ ਤੋਂ ਇਕ ਨਿਸ਼ਚਿਤ ਫ਼ਾਸਲੇ ਤੋਂ ਆਉਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਦੇ ਸੋਮੇ ਦੀ ਕਲਪਨਾ ਕਰੋ, ਜਿਵੇਂ ਕਿ ਕੋਈ ਅਜਿਹੇ ਤਾਰੇ ਦੀ, ਜਿਸ ਵਿੱਚੋਂ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਦੀ ਰਫ਼ਤਾਰ ਬੰਨ੍ਹਵੀਂ ਹੋਵੇ। ਜ਼ਾਹਰ ਹੈ ਕਿ ਸਾਡੇ ਨੇੜੇ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਦੀ ਰਫ਼ਤਾਰ ਐਨ ਉਸ ਰਫ਼ਤਾਰ ਦੇ ਬਰਾਬਰ ਜਾਪੇਗੀ, ਜਿਹੜੀ ਉਸ ਦੇ ਸੋਮੇਂ ਕੋਲ ਹੋਵੇਗੀ। (ਉਸ ਗ੍ਰਹਿ ਦਾ ਖਿਚ-ਪਾਊ ਪਿੜ ਬਹੁਤਾ ਵੱਡਾ ਨਹੀਂ ਹੋਵੇਗਾ, ਜਿਸ ਨਾਲ ਕੋਈ ਫ਼ਰਕ ਪੈ ਸਕਦਾ ਹੋਵੇ।) ਹੁਣ ਫ਼ਰਜ਼ ਕਰ ਲਓ ਕਿ ਸੋਮੇਂ ਵਾਲਾ ਤਾਰਾ ਸਾਡੇ ਵੱਲ ਆ ਰਿਹਾ ਹੈ। ਇਸ ਸੋਮੇ ਵਿੱਚੋਂ ਜਿਹੜੀ ਲਹਿਰ ਹੁਣ ਨਿਕਲੇਗੀ, ਉਹ ਸਾਡੇ ਨੇੜੇ ਹੋਵੇਗੀ। ਇਸ ਲਈ ਅਜਿਹੀ ਹਾਲਤ ਵਿੱਚ ਇਸ ਲਹਿਰ ਨੂੰ ਸਾਡੇ ਕੋਲ ਪਹੁੰਚਣ ਵਿੱਚ, ਇਕੋ ਥਾਂ ਟਿਕੇ ਹੋਏ ਤਾਰੇ ਵਿੱਚੋਂ ਆਉਣ ਵਾਲੀ ਲਹਿਰ ਦੇ ਟਾਕਰੇ ਵਿੱਚ ਘੱਟ ਸਮਾਂ ਲੱਗੇਗਾ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਦੋ ਲਹਿਰਾਂ ਦੇ ਟਾਕਰੇ ਵਿੱਚ ਘੱਟ ਸਮਾਂ ਲੱਗੇਗਾ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਦੋ ਲਹਿਰਾਂ ਦੇ ਪਹੁੰਚਣ ਵਾਲਾ ਸਮਾਂ ਬਹੁਤ ਵੱਡਾ ਹੈ, ਇਸ ਲਈ ਹਰ ਸਕਿੰਟ ਵਿੱਚ ਪਹੁੰਚਣ ਵਾਲੀਆਂ ਲਹਿਰਾਂ ਦੀ ਗਿਣਤੀ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੈ, ਇਕ ਟਿਕੇ ਹੋਏ ਤਾਰੇ ਦੀਆਂ ਲਹਿਰਾਂ ਦੇ ਟਾਕਰੇ ਵਿੱਚ। ਇਸ ਦੇ ਉਲਟ, ਜੇ ਰੌਸ਼ਨੀ ਦਾ ਸੋਮਾ ਸਾਥੋਂ ਦੂਰ ਜਾ ਰਿਹਾ ਹੋਵੇ, ਤਾਂ ਲਹਿਰਾਂ ਜੋ ਸਾਡੇ ਵੱਲ ਆ ਰਹੀਆਂ ਹਨ, ਉਨ੍ਹਾਂ ਦੀ ਰਫ਼ਤਾਰ ਘੱਟ ਹੋਵੇਗੀ। ਇਸ ਲਈ ਰੌਸ਼ਨੀ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਅਰਥ ਇਹ ਹੋਇਆ ਕਿ ਸਾਥੋਂ ਦੂਰ ਜਾਣ ਵਾਲੇ ਤਾਰਿਆਂ ਦੇ ਰੰਗ ਸੱਤਰੰਗੀ ਪੀਂਘ ਦੇ ਲਾਲ ਸਿਰੇ ਵੱਲ ਨਜ਼ਰ ਆਉਣਗੇ ਅਤੇ ਜਿਹੜੇ ਤਾਰੇ ਸਾਡੇ ਨੇੜੇ ਆ ਰਹੇ ਹੋਣਗੇ, ਉਨ੍ਹਾਂ ਦੇ ਰੰਗ ਨੀਲੇ ਸਿਰੇ ਵੱਲ ਨਜ਼ਰ ਆਉਣਗੇ, ਜਿਸ ਨੂੰ Doppler Effect ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਇਹ ਰੋਜ਼ਾਨਾ ਦੀ ਖੇਡ ਹੈ। ਸੜਕ ਉੱਤੇ ਜਾ ਰਹੀ ਕਾਰ ਦੀ ਗੂੰਜ ਸੁਣੋ; ਜਿਉਂ ਕਾਰ ਸਾਡੇ ਨੇੜੇ ਆ ਰਹੀ ਹੋਵੇ, ਇਹ ਗੂੰਜ ਬਹੁਤ ਉੱਚੀ ਹੋਵੇਗੀ (ਆਵਾਜ਼ ਦੀਆਂ ਲਹਿਰਾਂ ਦੀ ਰਫ਼ਤਾਰ ਵਾਂਗ) ਅਤੇ ਜਦੋਂ ਕਾਰ ਲੰਘ ਕੇ ਦੂਰ ਚਲੀ ਜਾਂਦੀ ਹੈ, ਇਸ ਦੀ ਗੂੰਜ ਮੱਧਮ ਹੁੰਦੀ ਜਾਂਦੀ ਹੈ। ਰੌਸ਼ਨੀ ਜਾਂ ਰੇਡੀਓ ਲਹਿਰਾਂ ਦਾ ਸੁਭਾਉ ਵੀ ਇਸ ਪ੍ਰਕਾਰ ਦਾ ਹੈ। ਅਸਲ ਵਿੱਚ ਪੁਲੀਸ ਕਾਰਾਂ ਦੀ ਸਪੀਡ ਦਾ ਨਿਰਣਾ Doppler Effect ਦੀ ਵਰਤੋਂ ਕਰਕੇ, ਅਰਥਾਤ ਰੇਡੀਓ ਲਹਿਰਾਂ ਨੂੰ ਮਿਣ ਕੇ ਕਰ ਲੈਂਦੀ ਹੈ। ਹੁਬੱਲ ਨੇ ਦੂਜੇ ਬ੍ਰਹਿਮੰਡਾਂ ਦੀ ਹੋਂਦ ਸਾਬਤ ਕਰਠ ਉਪਰੰਤ, ਆਪਣਾ ਸਮਾਂ ਉਨ੍ਹਾਂ ਦੇ ਫ਼ਾਸਲੇ ਅਤੇ ਸਤਰੰਗੀ ਪੀਂਘਾਂ ਦੀ ਸੂਚੀ ਤਿਆਰ ਕਰਨ ਲਈ ਵਰਤਿਆ। ਉਸ ਵੇਲੇ, ਬਹੁਤੇ ਲੋਕ, ਇਹ ਜਾਣਨ ਦੀ ਉਮੀਦ ਕਰਦੇ ਸਨ ਕਿ ਬ੍ਰਹਿਮੰਡ ਬਿਨਾਂ ਕਿਸੇ ਤਰਤੀਬ ਦੇ ਇਧਰ ਉਧਰ ਘੁੰਮਦੇ ਸਨ ਅਤੇ ਇਸ ਲਈ ਪੀਂਘਾਂ ਦੇ ਨੀਲੇ ਅਤੇ ਲਾਲ ਸਿਰੇ ਵੀ ਉਤਨੇ ਹੀ ਹੋਣਗੇ। ਇਸ ਲਈ, ਇਹ ਪਤਾ ਲੱਗਣ ਉੱਤੇ ਬਹੁਤੀ ਹੈਰਾਨੀ ਹੋਈ ਕਿ ਬਹੁਤੇ ਬ੍ਰਹਿਮੰਡ ਲਾਲ ਸਿਰੇ ਵੱਲ ਜਾਣ ਵਾਲੇ ਸਨ। ਤਕਰੀਬਨ ਸਾਰੇ ਹੀ ਸਾਥੋਂ ਦੂਰ ਜਾ ਸੀ ਸਨ। ਇਹ ਜਾਣ ਕੇ ਹੋਰ ਵੀ ਹੈਰਾਨੀ ਹੋਈ ਜਦੋਂ ਹੁਬੱਲ ਨੇ ਇਹ ਜਾਣਕਾਰੀ 1929 ਈ. ਵਿੱਚ ਪ੍ਰਕਾਸ਼ਤ ਕਰ ਦਿੱਤੀ। ਕਿਸੇ ਵੀ ਬ੍ਰਹਿਮੰਡ ਦੇ ਨਾਲ ਝੁਕਾਉ ਦਾ ਆਕਾਰ ਵੀ ਬੇਤਰਤੀਬਾ ਨਹੀਂ ਸੀ। ਸਗੋਂ ਇਹ ਆਕਾਰ ਉਸ ਬ੍ਰਹਿਮੰਡ ਦੀ ਸਾਥੋਂ ਦੂਰੀ (ਫ਼ਾਸਲੇ) ਉੱਤੇ ਨਿਰਭਰ ਸੀ। ਜਾਂ ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਕੋਈ ਬ੍ਰਹਿਮੰਡ ਸਾਥੋਂ ਜਿਤਨਾ ਜ਼ਿਆਦਾ ਦੂਰ ਹੈ, ਉਤਨੀ ਹੀ ਤੇਜ਼ ਰਫ਼ਤਾਰ ਨਾਲ ਦੂਰ ਜਾ ਰਿਹਾ ਹੈ। ਅਤੇ ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਸਾਡੀ ਧਰਤੀ ਇਕੋ ਥਾਂ ਟਿਕੀ ਹੋਈ ਨਹੀਂ ਹੈ, ਜਿਵੇਂ ਕਿ ਜਣਾ-ਖਣਾ ਐਉਂ ਸੋਚਦਾ ਹੁੰਦਾ ਸੀ। ਸਗੋਂ ਅਸਲ ਵਿੱਚ, ਇਹ ਤਾਂ ਫੈਲ ਰਹੀ ਹੈ—ਹਰ ਪਲ, ਭਿੰਨ-ਭਿੰਨ ਬ੍ਰਹਿਮੰਡਾਂ ਵਿਚਕਾਰ ਫ਼ਾਸਲੇ ਵੱਧ ਰਹੇ ਹਨ।

ਇਹ ਜਾਣਕਾਰੀ ਕਿ ਧਰਤੀ ਫੈਲ ਰਹੀ ਹੈ, ਵੀਹਵੀਂ ਸ਼ਤਾਬਦੀ ਦੇ ਮਹਾਨ ਬੋਧੀ ਪਰਿਵਰਤਨਾਂ ਵਿੱਚੋਂ ਇਕ ਸੀ। ਸਾਧਾਰਣ ਦ੍ਰਿਸ਼ਟੀ ਨਾਲ ਤਕਿਆਂ, ਇਹ ਖ਼ੁਸ਼ੀ ਭਰੀ ਹੈਰਾਨੀ ਹੈ ਕਿ ਇਹ ਗੱਲ ਪਹਿਲਾਂ ਕਿਸੇ ਨੇ ਵੀ ਕਿਉਂ ਨਹੀਂ ਸੀ ਸੋਚੀ। ਨਿਊਟਨ ਅਤੇ ਹੋਰਨਾਂ ਨੂੰ ਇਹ ਸਮਝ ਪੈ ਜਾਣੀ ਚਾਹੀਦੀ ਸੀ ਕਿ ਇਕੋ ਥਾਂ ਟਿਕੀ ਹੋਈ ਧਰਤੀ ਤਾਂ ਛੇਤੀ, ਖਿੱਚ-ਪਾਊ ਸ਼ਕਤੀ ਸਦਕਾ ਸੁੰਘੜਨੀ ਸ਼ੁਰੂ ਹੋ ਜਾਣੀ ਚਾਹੀਦੀ ਸੀ। ਪਰੰਤੂ ਧਰਤੀ ਤਾਂ ਫੈਲ ਰਹੀ ਹੈ। ਜੇ ਇਹ ਹੌਲੀ-ਹੌਲੀ ਫੈਲ ਰਹੀ ਹੈ ਤਾਂ ਖਿੱਚ-ਪਾਊ ਸ਼ਕਤੀ ਸਦਕਾ ਇਹ ਫੈਲਣੀ ਬੰਦ ਹੋ ਜਾਂਦੀ ਅਤੇ ਸੁੰਗੜਨੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀ। ਪਰੰਤੂ ਜੇ ਇਕ ਖ਼ਾਸ ਰਫ਼ਤਾਰ ਨਾਲੋਂ ਤੇਜ਼ੀ ਨਾਲ ਫੈਲ ਰਹੀ ਹੈ, ਖਿੱਚ-ਸ਼ਕਤੀ ਇਸ ਨੂੰ ਵਧਣੋਂ ਰੋਕਣ ਜੋਗੀ ਕਦੇ ਵੀ ਬਲਵਾਨ ਨਹੀਂ ਹੋ ਸਕੇਗੀ ਅਤੇ ਧਰਤੀ ਸਦਾ ਹੀ ਫੈਲਦੀ ਰਹੇਗੀ। ਜਦੋਂ ਧਰਤੀ ਦੀ ਸਤਹ ਤੋਂ ਕੋਈ ਇਕ ਰੌਕਟ ਉੱਪਰ ਨੂੰ ਚੜ੍ਹਦਾ ਹੈ, ਤਾਂ ਇਹੋ ਕੁਝ ਵਾਪਰਿਆ ਕਰਦਾ ਹੈ। ਜੇ ਇਸ ਦੇ ਵਧਣ ਦੀ ਰਫ਼ਤਾਰ ਮੱਧਮ ਹੈ, ਤਾਂ ਖਿੱਚ-ਸ਼ਕਤੀ ਉਸ ਰੌਕਟ ਨੂੰ ਰੋਕ ਲਵੇਗੀ ਅਤੇ ਉਹ ਧਰਤੀ ਵੱਲ ਡਿੱਗਣਾ ਸ਼ੁਰੂ ਕਰ ਦੇਵੇਗਾ। ਦੂਜੇ ਬੰਨੇ, ਜੇ ਰੌਕਟ ਇਕ ਖ਼ਾਸ ਰਫ਼ਤਾਰ ਨਾਲੋਂ ਵੀ ਤੇਜ਼ੀ ਨਾਲ ਜਾ ਰਿਹਾ ਹੋਵੇ, (ਤਕਰੀਬਨ ਸੱਤ ਮੀਲ ਪ੍ਰਤੀ ਸਕਿੰਟ), ਤਾਂ ਖਿੱਚ-ਸ਼ਕਤੀ ਉਸ ਨੂੰ ਥੱਲੇ ਖਿੱਚਣ ਜੋਗੀ ਬਲਵਾਨ ਨਹੀਂ ਹੋਵੇਗੀ ਅਤੇ ਉਹ ਸਦਾ ਧਰਤੀ ਤੋਂ ਦੂਰ ਜਾਂਦਾ ਰਹੇਗਾ। ਧਰਤੀ ਦੇ ਇਸ ਸੁਭਾ ਦਾ ਪਤਾ ਤਾਂ ਨਿਊਟਨ ਦੀ ਖਿੱਚ-ਸ਼ਕਤੀ ਦੇ ਸਿਧਾਂਤ ਸਦਕਾ, ਉੱਨੀਵੀਂ, ਅਠਾਰਵੀਂ ਜਾਂ ਸਤਾਰ੍ਹਵੀਂ ਸ਼ਤਾਬਦੀ ਦੇ ਅੰਤ ਵਿੱਚ ਕਿਸੇ ਵੇਲੇ ਵੀ ਜਾਣਿਆ ਜਾ ਸਕਦਾ ਸੀ। ਪਰੰਤੂ ਧਰਤੀ ਦੇ ਅਚੱਲ ਹੋਣ ਬਾਰੇ ਵਿਸ਼ਵਾਸ ਇਤਨਾ ਪੱਕਾ ਸੀ ਕਿ ਇਹ ਜਾਣਕਾਰੀ ਵੀਹਵੀਂ ਸਦੀ ਦਾ ਵਿਸ਼ਾ ਬਣ ਗਈ। ਆਈਨਸਟਾਈਨ ਵੀ, ਜਦੋਂ ਉਸ ਨੇ ਅਨੁਪਾਤ ਦਾ ਆਮ ਸਿਧਾਂਤ 1915 ਵਿੱਚ ਪੜ੍ਹਿਆ ਸੀ, ਇਸ ਵਿਸ਼ਵਾਸ ਦਾ ਪੱਕਾ ਧਾਰਨੀ ਸੀ ਕਿ ਧਰਤੀ ਅਚੱਲ਼ ਹੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਕਿ ਉਸ ਨੇ ਆਪਣੇ ਸਿਧਾਂਤ ਵਿੱਚ ਸੋਧ ਕਰਕੇ ਅਜਿਹੀ ਸੰਭਾਵਨਾ ਸਾਬਤ ਕਰਨ ਲਈ ਆਪਣੇ ਹਿਸਾਬ ਵਿੱਚ ਇਕ ਨਵੀਂ ਕਲਪਤ ਸ਼ਕਤੀ ਪੇਸ਼ ਕਰ ਦਿੱਤੀ ਸੀ, ਜਿਹੜੀ ਹੋਰ ਸ਼ਕਤੀਆਂ ਵਾਂਗ ਕਿਸੇ ਖ਼ਾਸ ਸੋਮੇ ਤੋਂ ਨਹੀਂ ਸੀ ਆਉਂਦੀ, ਸਗੋਂ ਸੱਚਾਈ ਦੇ ਸੋਮੇਂ ਦੇ ਤਾਣੇ-ਬਾਣੇ ਵਿੱਚ ਹੀ ਮੌਜੂਦ ਸੀ। ਉਸ ਨੇ ਇਹ ਦਾਅਵਾ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਸਥਾਨ/ਸਮਾਂ ਆਪਣੇ ਆਪ ਹੀ ਫੈਲਣ ਦੇ ਸੁਭਾ ਵਾਲਾ ਹੈ। ਇਸ ਨੂੰ ਧਰਤੀ ਉੱਤੇ ਸਮੂਹਕ ਪਦਾਰਥਾਂ ਦੀ ਸ਼ਕਤੀ ਦੀ ਖਿੱਚ ਦੇ ਤੁਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਤਾਂ ਜੋ ਨਤੀਜੇ ਵਜੋਂ ਇਕ ਅਚੱਲ ਧਰਤੀ ਕਾਇਮ ਹੋ ਜਾਵੇ। ਐਉਂ ਜਾਪਦਾ ਹੈ ਕੇਵਲ ਇਕੋ ਬੰਦਾ, ਹੀ ਅਨੁਪਾਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਨੂੰ ਉਪਰੋਂ-ਉਪਰੋਂ ਮੰਨਣ ਲਈ ਤਿਆਰ ਸੀ ਅਤੇ ਜਦੋਂ ਆਈਨਸਟਾਈਨ ਅਤੇ ਹੋਰ ਫਿਜ਼ਿਕਸ ਵਿਗਿਆਨੀ, ਆਮ ਅਨੁਪਾਤਕ ਸਿਧਾਂਤ ਦੇ ਆਮ ਸਿਧਾਂਤ ਤੋਂ ਬਚਣ ਲਈ ਢੰਗ ਲਭ ਰਹੇ ਸਨ, ਕਿ ਜਿਸ ਦੁਆਰਾ ਚਲਦੀ ਫਿਰਦੀ ਧਰਤੀ ਮੰਨੀ ਜਾਂਦੀ ਸੀ। ਰੂਸ ਦੇ ਫਿਜ਼ਿਕਸ ਵਿਗਿਆਨੀ ਅਤੇ ਗਣਿਤ ਦੇ ਮਾਹਿਰ ਅਲੈਗਜ਼ੈਂਡਰ ਫਰਾਈਡਮੈਨ (Alexander Friedmann) ਨੇ, ਇਸ ਦੀ ਵਿਆਖਿਆ ਹੀ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀ ਸੀ।

ਫਰਾਈਡਮੈਨ ਨੇ ਧਰਤੀ ਬਾਰੇ ਦੋ ਗੱਲਾਂ ਫ਼ਰਜ਼ ਕੀਤੀਆਂ ਸਨ ਕਿ ਕਿਸੇ ਪਾਸਿਓਂ ਵੀ ਤੱਕੀਏ, ਧਰਤੀ ਇਕੋ ਜਿਹੀ ਜਾਪਦੀ ਹੈ ਅਤੇ ਕਿਹਾ ਕਿ ਇਹ ਗੱਲ ਉਦੋਂ ਵੀ ਸੱਚੀ ਸਿੱਧ ਹੋਵੇਗੀ, ਜਦੋਂ ਅਸੀਂ ਧਰਤੀ ਨੂੰ ਕਿਸੇ ਹੋਰ ਅਸਥਾਨ ਤੋਂ ਤਕਾਂਗੇ। ਫਰਾਈਡਮੈਨ ਦੀਆਂ ਕੇਵਲ ਇਨ੍ਹਾਂ ਦੋ ਵਿਚਾਰਾਂ ਨੇ ਹੀ ਜ਼ਾਹਰ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਸਾਨੂੰ ਇਹ ਉਮੀਦ ਨਹੀਂ ਕਰਨੀ ਚਾਹੀਦੀ ਕਿ ਧਰਤੀ ਇਕੋ ਥਾਂ ਖਲੋਤੀ ਹੈ। ਅਸਲ ਵਿੱਚ, ਐਡਵਿਨ ਹੁਬੱਲ ਦੀ ਖੋਜ ਤੋਂ ਕਈ ਵਰ੍ਹੇ ਪਹਿਲਾਂ ਹੀ, 1922 ਵਿੱਚ ਫਰਾਈਡਮੈਨ ਨੇ ਐਨ ਉਹ ਕੁਝ ਪ੍ਰਗਟ ਕਰ ਦਿੱਤਾ ਸੀ, ਜੋ ਕੁਝ ਹੁਬੱਲ ਨੇ ਮਾਲੂਮ ਕੀਤਾ ਸੀ।

ਇਹ ਤਜਵੀਜ ਕਿ ਧਰਤੀ ਹਰ ਪਾਸਿਓਂ ਇਕੋ ਜਿਹੀ ਪ੍ਰਤੀਤ ਹੁੰਦੀ ਹੈ, ਅਸਲ ਵਿੱਚ ਸੱਚ ਅਤੇ ਦਰੁੱਸਤ ਨਹੀਂ ਹੈ। ਉਦਾਹਰਣ ਵਜੋਂ, ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਦੇਖ ਚੁੱਕੇ ਹਾਂ, ਸਾਡੇ ਬ੍ਰਹਿਮੰਡ ਦੇ ਦੂਜੇ ਤਾਰੇ, ਰਾਤ ਵੇਲੇ, ਆਕਾਸ਼ ਵਿੱਚ, ਰੌਸ਼ਨੀ ਦਾ ਇਕ ਵੱਖਰਾ ਝੁਰਮਟ ਬਣਾਉਂਦੇ ਹਨ। ਜਿਸ ਨੂੰ ਅਸੀਂ ਮਿਲਕੀ ਵੇ ਕਹਿੰਦੇ ਹਾਂ। ਪਰੰਤੂ ਜੇ ਅਸੀਂ ਦੂਰ- ਦੁਰਾਡੇ ਬ੍ਰਹਿਮੰਡਾਂ ਨੂੰ ਦੇਖੀਏ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਲਗਭਗ ਇਕੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ। ਇਸ ਲਈ ਧਰਤੀ ਹਰ ਪਾਸੇ ਅੰਦਾਜ਼ਨ ਇਕੋ ਜਿਹੀ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਜੇ ਕੋਈ ਇਸ ਨੂੰ ਬ੍ਰਹਿਮੰਡਾਂ ਦੇ ਵਿਚਲੇ ਫ਼ਾਸਲਿਆਂ ਨੂੰ ਨਜ਼ਰ-ਅੰਦਾਜ਼ ਕਰ ਦੇਵੇ। ਬਹੁਤ ਲੰਮੇ ਸਮੇਂ ਤੱਕ, ਫਰਾਈਡਮੈਨ ਦੀ ਇਸ ਤਜਵੀਜ਼ ਨੂੰ ਸਹੀ ਮੰਨਿਆ ਜਾਂਦਾ ਰਿਹਾ ਸੀ, ਜਿਸ ਅਨੁਸਾਰ ਅਸਲੀ ਧਰਤੀ ਦੇ ਨੇੜੇ-ਤੇੜੇ ਅੰਦਾਜ਼ਾ ਲਾਇਆ ਗਿਆ ਸੀ । ਪਰੰਤੂ ਹੁਣੇ-ਹੁਣੇ ਪਿੱਛੇ ਜਿਹੇ, ਇਕ ਭਾਗਸ਼ਾਲੀ ਹਾਦਸੇ ਨੇ ਇਹ ਸੱਚਾਈ ਜ਼ਾਹਰ ਕਰ ਦਿੱਤੀ ਕਿ ਫਰਾਈਡਮੈਨ ਵੱਲੋਂ ਧਰਤੀ ਦੀ ਵਿਆਖਿਆ ਬਹੁਤ ਜ਼ਿਆਦਾ ਠੀਕ ਅਤੇ ਸਹੀ ਹੈ।

1965 ਵਿੱਚ, ਅਮਰੀਕਾ ਦੇ ਦੋ ਫਿਜ਼ਿਕਸ ਵਿਗਿਆਨੀ, Bell Telephone Lab ਜੋ ਕਿ ਨਿਊ ਜਰਸੀ ਵਿੱਚ ਸਥਿਤ ਹੈ, Arno Penzias ਅਤੇ ਰੋਬਰਟ ਵਿਲਸਨ ਮਾਈਕਰੋ-ਵੇਵ ਦੇ ਇਕ ਤੇਜ਼ ਪੜਤਾਲੀ ਜੰਤਰ ਦੀ ਪਰਖ ਕਰ ਰਹੇ ਸਨ। (ਮਾਈਕਰੋ- ਵੇਵ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਵਰਗੀਆਂ ਹੀ ਹੁੰਦੀਆਂ ਹਨ), ਪਰੰਤੂ ਉਨ੍ਹਾਂ ਦੀ ਰਫ਼ਤਾਰ ਇਕ ਕਰੋੜ ਲਹਿਰਾਂ ਪ੍ਰਤੀ ਸਕਿੰਟ ਹੋਇਆ ਕਰਦੀ ਹੈ। Penzia ਅਤੇ ਵਿਲਸਨ ਉਦੋਂ ਬਹੁਤ ਘਬਰਾ ਗਏ ਜਦੋਂ ਉਨ੍ਹਾਂ ਨੇ ਦੇਖਿਆ ਕਿ ਉਨ੍ਹਾਂ ਦੇ (Detector) ਸ਼ੋਰ ਵਿੱਚ ਬੇਲੋੜਾ ਵਾਧਾ ਹੋ ਜਾਂਦਾ ਸੀ। ਇਹ ਸ਼ੋਰ ਕਿਸੇ ਖ਼ਾਸ ਪਾਸਿਓਂ ਆਉਂਦਾ ਨਹੀਂ ਸੀ ਜਾਪਦਾ। ਪਹਿਲਾਂ ਉਨ੍ਹਾਂ ਨੇ (Detector) ਵਿੱਚ ਪੰਛੀਆਂ ਦੀਆਂ ਡਿੱਗੀਆਂ ਹੋਈਆਂ ਬਿੱਠਾਂ ਦੇਖੀਆਂ। ਅਤੇ ਹੋਰ ਵੀ ਨੁਕਸ ਲੱਭਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਪਰ ਇਨ੍ਹਾਂ ਦਾ ਕੋਈ ਅਸਰ ਨਹੀਂ ਸੀ ਹੋਇਆ। ਉਹ ਜਾਣਦੇ ਸਨ ਕਿ ਵਾਯੂ-ਮੰਡਲ ਵਿੱਚੋਂ ਆਉਣ ਵਾਲਾ ਸ਼ੋਰ ਉਸ ਵੇਲੇ ਵੱਧ ਹੋਵੇਗਾ, ਜਦੋਂ ਉਸ ਦਾ ਮੂੰਹ ਉੱਪਰ ਨੂੰ ਨਾ ਹੋਵੇ ਅਤੇ ਜੇ ਉੱਪਰ ਨੂੰ ਨਾ ਹੋਵੇ ਤਾਂ ਸ਼ੋਰ ਘੱਟ ਜਾਵੇਗਾ, ਕਿਉਂਕਿ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਨੂੰ ਉਸ ਵੇਲੇ ਵਧੇਰੇ ਵਾਯੂ ਮੰਡਲ ਵਿੱਚੋਂ ਲੰਘਣਾ ਪੈਂਦਾ ਹੈ, ਜਦੋਂ ਦਿਸ-ਹੱਦੇ ਕੋਲੋਂ ਆਉਣ ਅਤੇ ਜਦੋਂ ਸਿਰ ਉੱਪਰੋਂ ਆਉਣ, ਤਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਘੱਟ ਵਾਯੂ-ਮੰਡਲ ਵਿੱਚੋਂ ਲੰਘਣਾ ਪੈਂਦਾ ਹੈ। ਡਿਟੈਕਟਰ ਦੀ ਆਵਾਜ਼ ਵਿੱਚ, ਉਸ ਦੀ ਦਿਸ਼ਾ ਬਦਲਣ ਨਾਲ ਕੋਈ ਫ਼ਰਕ ਨਹੀਂ ਸੀ ਪੈ ਰਿਹਾ। ਇਸ ਲਈ ਇਹ ਸਪੱਸ਼ਟ ਹੀ ਸੀ ਕਿ ਇਸ ਦੀ ਆਵਾਜ਼ ਵਾਯੂ-ਮੰਡਲ ਵਿੱਚੋਂ ਲੰਘ ਕੇ ਨਹੀਂ ਸੀ ਆ ਰਹੀ। ਰਾਤ ਵੇਲੇ ਅਤੇ ਦਿਨ ਵੇਲੇ ਵੀ ਇਕੋ ਰਹਿੰਦੀ ਸੀ ਅਤੇ ਸਾਰਾ ਸਾਲ ਇਕੋ ਰਹਿੰਦੀ ਸੀ। ਬੇਸ਼ੱਕ ਧਰਤੀ ਆਪਣੇ ਧੁਰੇ ਉੱਤੇ ਵੀ ਘੁੰਮ ਰਹੀ ਸੀ ਅਤੇ ਸੂਰਜ ਦੇ ਦੁਆਲੇ ਵੀ ਚੱਕਰ ਲਾ ਰਹੀ ਸੀ। ਇਸ ਤੋਂ ਇਹ ਪਤਾ ਲੱਗ ਗਿਆ ਕਿ ਰੇਡੀਏਸ਼ਨ (ਆਵਾਜ਼) ਸੂਰਜ ਮੰਡਲ ਦੇ ਬਾਹਰੋਂ ਆ ਰਹੀ ਸੀ, ਸਗੋਂ ਬ੍ਰਹਿਮੰਡ ਤੋਂ ਵੀ ਬਾਹਰੋਂ ਨਹੀਂ, ਇਸ ਵਿੱਚ ਫ਼ਰਕ ਪੈਣਾ ਜ਼ਰੂਰੀ ਸੀ ਕਿਉਂਕਿ ਧਰਤੀ ਦੀ ਹਰਕਤ ਸਦਕਾ ਡਿਟੈਕਟਰ ਦਾ ਮੂੰਹ ਭਿੰਨ- ਭਿੰਨ ਦਿਸ਼ਾਵਾਂ ਵੱਲ ਮੁੜੀ ਜਾਂਦਾ ਸੀ। ਅਸਲ ਵਿੱਚ, ਸਾਨੂੰ ਪਤਾ ਹੈ ਕਿ ਰੇਡੀਏਸ਼ਨ (ਆਵਾਜ਼) ਨਜ਼ਰ ਆ ਰਹੀ ਧਰਤੀ ਤੋਂ ਬਾਹਰੋਂ ਹੀ ਸਾਡੇ ਵੱਲ ਆ ਰਹੀ ਹੋਵੇਗੀ, ਕਿਉਂਕਿ ਦਿਸ਼ਾਵਾਂ ਬਦਲਣ ਨਾਲ ਵੀ ਇਸ ਵਿੱਚ ਕੋਈ ਫ਼ਰਕ ਨਹੀਂ ਪੈਂਦਾ ਅਤੇ ਧਰਤੀ ਵੀ ਸਾਰੇ ਪਾਸੀਂ ਇਕੋ ਜਿਹੀ ਹੋਵੇਗੀ, ਭਾਵੇਂ ਵੱਡੇ ਪੈਮਾਨੇ ‘ਤੇ ਹੀ ਸਹੀ। ਸਾਨੂੰ ਹੁਣ ਪਤਾ ਲੱਗ ਗਿਆ ਹੈ ਕਿ ਅਸੀਂ ਭਾਵੇਂ ਕਿਸੇ ਪਾਸੇ ਨਜ਼ਰ ਮਾਰੀਏ, ਇਸ ਆਵਾਜ਼ ਵਿੱਚ ਦਸ ਹਜ਼ਾਰ ਪਿੱਛੇ ਇਕ ਹਿੱਸੇ ਨਾਲੋਂ ਵੱਧ ਫ਼ਰਕ ਨਹੀਂ ਪੈਂਦਾ। ਇਸ ਲਈ Penzia ਅਤੇ ਵਿਲਸਨ ਨੂੰ

Friedman ਦੇ ਪਹਿਲੇ ਸੁਝਾਉ ਦੀ ਮੱਲੋ-ਮੱਲੀ ਸਹੀ-ਸਹੀ ਪੁਸ਼ਟੀ ਕਰਨੀ ਪੈ ਗਈ ਸੀ। ਉਨ੍ਹਾਂ ਦਿਨਾਂ ਵਿੱਚ ਹੀ, ਨਜ਼ਦੀਕੀ ਪ੍ਰਿਨਸਟਨ (Princeton) ਯੂਨੀਵਰਸਿਟੀ ਦੇ ਦੋ ਫ਼ਿਜਿਕਸ ਮਾਹਰ Bob Dicke ਅਤੇ Jim Peebles ਵੀ ਮਾਈਕਰੋਂ ਵੇਵ ਵਿੱਚ ਇਲਚਸਪੀ ਲੈ ਰਹੇ ਸਨ। ਉਹ ਅਲੈਗਜ਼ੈਂਡਰ ਫਰਾਈਡਮੈਨ’ਦੇ ਚੇਲੇ ਜਾਰਜ ਗੈਮੋਂ (George Gamow) ਦੀ ਤਜਵੀਜ਼ ਅਨੁਸਾਰ ਕੰਮ ਕਰ ਰਹੇ ਸਨ, ਤਜਵੀਜ਼ ਇਹ ਸੀ ਕਿ ਧਰਤੀ ਕਿਸੇ ਸਮੇਂ ਬਹੁਤ ਤੱਤੀ ਅਤੇ ਸੰਘਣੀ ਹੋਵੇਗੀ ਅਤੇ ਇਸ ਦੀ ਚਮਕ ਤੱਤੀ ਅਤੇ ਚਿੱਟੀ ਹੋਵੇਗੀ। ਡਿੱਕ ਅਤੇ ਪੀਬਲ ਦੀ ਦਲੀਲ ਸੀ ਕਿ ਹਾਲੇ ਵੀ ਉਨ੍ਹਾਂ ਨੂੰ ਪਹਿਲੀ ਧਰਤੀ ਦੀ ਚਮਕ ਦੇਖ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ ਕਿਉਂਕਿ ਇਸ ਦੇ ਦੂਰ-ਦੁਰਾਡੇ ਹਿੱਸਿਆਂ ਵਿੱਚੋਂ ਰੌਸ਼ਨੀ ਸਾਡੇ ਕੋਲ ਪਹੁੰਚਣ ਵਾਲੀ ਹੋਵੇਗੀ। ਪਰੰਤੂ ਧਰਤੀ ਦੇ ਫੈਲਣ ਦਾ ਅਰਥ ਹੈ ਕਿ ਇਹ ਰੌਸ਼ਨੀ ਇਤਨੀ ਜ਼ਿਆਦਾ ਲਾਲ ਰੰਗ ਦੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਇਹ ਸਾਨੂੰ ਮਾਈਕਰੋ ਵੇਵ ਰੇਡੀਏਸ਼ਨ ਵਰਗੀ ਨਜ਼ਰ ਆਉਣੀ ਚਾਹੀਦੀ ਹੈ। ਡਿੱਕ ਅਤੇ ਪੀਬਲ ਹਾਲੇ ਅਜਿਹੀ ਰੇਡੀਏਸ਼ਨ ਨੂੰ ਦੇਖਣ ਦੀ ਤਿਆਰੀ ਹੀ ਕਰ ਰਹੇ ਸਨ, ਜਦੋਂ Penzias ਅਤੇ Wilson ਨੇ ਉਨ੍ਹਾਂ ਦੇ ਕੰਮ ਬਾਰੇ ਸੁਣ ਲਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨੇ ਅਨੁਭਵ ਕਰ ਲਿਆ .ਸੀ ਕਿ ਉਨ੍ਹਾਂ ਨੂੰ ਅਜਿਹੀ ਰੇਡੀਏਸ਼ਨ ਦਾ ਪਹਿਲਾਂ ਹੀ ਪਤਾ ਲੱਗ ਚੁੱਕਾ ਸੀ। ਇਸ ਪ੍ਰਾਪਤੀ ਲਈ, ਪੈਨਜ਼ੀਆ ਅਤੇ ਵਿਲਸਨ ਨੂੰ 1978 ਵਿੱਚ ਨੋਬਲ ਪੁਰਸਕਾਰ ਮਿਲ ਗਿਆ ਸੀ (ਜਾਪਦਾ ਹੈ ਕਿ ਇਸ ਮਾਮਲੇ ਵਿੱਚ ਡਿੱਕ ਅਤੇ ਪੀਬਲਜ਼ ਨਾਲ ਜ਼ਿਆਦਤੀ ਹੋ ਗਈ ਸੀ। ਵਿਚਾਰੇ ਗੈਮੋ (Gamow) ਦਾ ਨਾਮ ਹੀ ਕੀ ਲੈਣਾ ਹੈ)।

ਹੁਣ ਪਹਿਲੀ ਨਜ਼ਰੇ, ਇਹ ਜਾਣਕਾਰੀ ਕਿ ਧਰਤੀ, ਕਿਸੇ ਪਾਸਿਉਂ ਵੀ ਇਸ ਨੂੰ ਦੇਖੀਏ, ਇਕੋ ਜਿਹੀ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਐਉਂ ਸੋਝੀ ਪੈਂਦੀ ਹੈ ਕਿ ਧਰਤੀ ਉੱਤੇ ਸਾਡੇ ਆਪਣੇ ਅਸਥਾਨ ਦੀ ਕੋਈ ਵਿਸ਼ੇਸ਼ਤਾ ਜ਼ਰੂਰ ਹੈ। ਖ਼ਾਸ ਕਰਕੇ, ਜੇ ਅਸੀਂ ਇਹ ਅਨੁਭਵ ਕਰੀਏ ਕਿ ਹੋਰ ਸਾਰੇ ਬ੍ਰਹਿਮੰਡ ਸਾਥੋਂ ਦੂਰ ਜਾ ਰਹੇ ਹਨ, ਤਾਂ ਸਾਡਾ ਅਸਥਾਨ ਧਰਤੀ ਦਾ ਕੇਂਦਰ ਹੋਵੇਗਾ। ਇਸ ਦੇ ਮੁਕਾਬਲੇ ਦੀ ਇਕ ਹੋਰ ਵਿਆਖਿਆ ਵੀ ਹੈ, ਕਿ ਧਰਤੀ ਨੂੰ ਜੇ ਦੂਜੇ ਬ੍ਰਹਿਮੰਡਾਂ ਤੋਂ ਜਾ ਕੇ ਦੇਖੀਏ ਤਾਂ ਵੀ ਇਹ ਹਰ ਦਿਸ਼ਾ ਤੋਂ ਇਕੋ ਜਿਹੀ ਪ੍ਰਤੀਤ ਹੋਵੇਗੀ। ਇਹ, ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਪਹਿਲਾਂ ਦੇਖ -ਹੀ ਚੁੱਕੇ ਹਾਂ, ਫਰਾਇਡਮੈਨ ਦੀ ਦੂਜੀ ਤਜਵੀਜ਼ ਹੈ। ਅਸੀਂ ਅਜਿਹਾ ਵਿਸ਼ਵਾਸ ਸਹਿਜ ਦੇ ਆਧਾਰ ਉੱਤੇ ਹੀ ਕਰ ਰਹੇ ਹਾਂ। ਇਹ ਹੋਰ ਵੀ ਚੰਗਾ ਹੋਵੇ ਜੇ ਧਰਤੀ ਸਾਡੇ ਆਲੇ-ਦੁਆਲੇ ਦੇਖਿਆਂ ਹੀ ਚਾਰੇ ਪਾਸਿਉਂ ਇਕੋ ਜਿਹੀ ਨਜ਼ਰ ਆਵੇ, ਪਰੰਤੂ ਇਹ ਹੋਰ ਥਾਵਾਂ ਤੋਂ ਅਜਿਹੀ ਨਜ਼ਰ ਨਾ ਆਵੇ। ਫ਼ਰਾਇਡਮੈਨ ਦੇ ਕਥਨ ਅਨੁਸਾਰ, ਸਾਰੇ ਹੀ ਮੰਡਲ ਇਕ ਦੂਜੇ ਤੋਂ ਦੂਰ ਜਾ ਰਹੇ ਹਨ। ਇਹ ਉਸ ਗੁਬਾਰੇ ਵਰਗੀ ਗੱਲ ਹੈ, ਜਿਸ ਦੇ ਉੱਤੇ ਕਈ ਧੱਬੇ ਲਾ ਕੇ ਹਵਾ ਵਿੱਚ ਉਡਾ ਦਿੱਤਾ ਜਾਵੇ। ਜਿਉਂ-ਜਿਉਂ ਗੁਬਾਰਾ ਫੈਲਦਾ ਜਾਂਦਾ ਹੈ, ਤਿਉਂ-ਤਿਉਂ ਧੱਬਿਆਂ ਵਿਚਕਾਰਲਾ ਫ਼ਾਸਲਾ ਵੀ ਵਧੀ ਜਾਂਦਾ ਹੈ, ਪਰੰਤੂ ਕਿਸੇ ਧੱਬੇ ਨੂੰ ਵੀ ਉਸ ਫੈਲਾਓ ਦਾ ਕੇਂਦਰ ਨਹੀਂ ਮੰਨਿਆ ਜਾ ਸਕਦਾ। ਉੱਪਰੋਂ, ਧੱਬਿਆਂ ਦਾ ਪਾੜਾ ਜਿਵੇਂ-ਜਿਵੇਂ ਵੱਧਦਾ ਜਾਵੇਗਾ, ਤਿਵੇਂ-ਤਿਵੇਂ ਉਹ ਇਕ ਦੂਜੇ ਤੋਂ ਤੇਜ਼ੀ ਨਾਲ ਦੂਰ ਹੁੰਦੇ ਜਾਣਗੇ। ਇਸੇ ਪ੍ਰਕਾਰ, ਫਰਾਈਡਮੈਨ ਦੇ ਕਥਨ ਅਨੁਸਾਰ, ਜਿਸ ਰਫ਼ਤਾਰ ਨਾਲ ਕੋਈ ਦੋ ਧਰਤੀਆਂ ਦੂਰ ਹੋ ਰਹੀਆਂ ਹੋਣ, ਉਸੇ ਹਿਸਾਬ ਨਾਲ ਉਨ੍ਹਾਂ ਦਾ ਆਪਸੀ ਫ਼ਾਸਲਾ ਵੀ ਵੱਧ ਜਾਵੇਗਾ। ਇਸ ਲਈ ਇਹ ਸਪੱਸ਼ਟ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿ ਕਿਸੇ ਬ੍ਰਹਿਮੰਡ ਦੀ ਪੀਂਘ ਦਾ ਲਾਲ ਸਿਰਾ, ਉਸ ਬ੍ਰਹਿਮੰਡ ਅਤੇ ਸਾਡੇ ਵਿਚਕਾਰ ਫ਼ਾਸਲਾ ਉਸ ਦੇ ਫ਼ਾਸਲੇ ਦੇ ਬਰਾਬਰ ਹੀ ਹੋਵੇਗਾ, ਐਨ ਹੁਬੱਲ ਦੀ ਖੋਜ ਦੇ ਬਰਾਬਰ। ਫਰਾਈਡਮੈਨ ਦੀ ਖੋਜ ਦੀ ਸਫ਼ਲਤਾ ਦੇ ਬਾਵਜੂਦ ਕਿ ਉਸ ਨੇ ਹੁਬੱਲ ਦੀ ਖੋਜ ਵੱਲ ਸੰਕੇਤ ਦਿੱਤਾ ਸੀ। ਉਸ ਦੀ ਪ੍ਰਾਪਤੀ ਦਾ ਰਾਜ਼ ਪੱਛਮ ਵਿੱਚ ਛੁਪਿਆ ਹੀ ਰਿਹਾ ਸੀ, ਜਦੋਂ ਤੱਕ 1935 ਈ: ਵਿੱਚ ਇਸੇ ਪ੍ਰਕਾਰ ਦੀਆਂ ਖੋਜਾਂ, ਅਮਰੀਕਾ ਦੇ ਫਿਜ਼ਿਕਸ ਦੇ ਮਾਹਰ ਹਾਵਰਡ ਰੌਬਰਟਸਨ (Howard Robertson) ਅਤੇ ਬਰਤਾਨਵੀਂ ਹਿਸਾਬ ਦਾਨ (Arthenr Wolker) ਅਰਥਰ ਵਲਕਰ ਨੇ ਨਹੀਂ ਸਨ ਕਰ ਲਈਆਂ, ਜੋ ਹੁਬੱਲ ਦੀ ਇਸ ਖੋਜ ਉੱਤੇ ਆਧਾਰਿਤ ਸਨ ਕਿ ਧਰਤੀ ਵਿੱਚ ਇਕੋ ਜਿਹਾ ਫੈਲਾਓ ਹੋ ਰਿਹਾ ਹੈ।

ਭਾਵੇਂ ਫਰਾਈਡਮੈਨ ਨੇ ਤਾਂ ਇਕ ਗੁਰ ਲੱਭਿਆ ਸੀ, ਉਸ ਦੀਆਂ ਦੋ ਮੁੱਢਲੀਆਂ ਤਜਵੀਜ਼ਾਂ ਦੇ ਨਾਲ ਮੇਲ ਖਾਣ ਵਾਲੇ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਗੁਰ ਮੌਜੂਦ ਹਨ। ਪਹਿਲੇ ਗੁਰ (ਜੋ ਫਰਾਈਡਮੈਨ ਨੇ ਲੱਭਿਆ ਸੀ) ਅਨੁਸਾਰ ਧਰਤੀ ਬਹੁਤ ਹੌਲੀ-ਹੌਲੀ ਫੈਲ ਰਹੀ ਸੀ ਕਿ ਜਿਸ ਕਾਰਨ ਕਰਕੇ ਦੋ ਬ੍ਰਹਿਮੰਡਾਂ ਦੇ ਵਿਚਕਾਰਲੀ ਖਿੱਚ ਸ਼ਕਤੀ ਸਦਕਾ, ਉਨ੍ਹਾਂ ਦਾ ਫੈਲਾਉ ਵੀ ਹੌਲੀ-ਹੌਲੀ ਹੁੰਦਾ ਹੈ, ਅਤੇ ਅੰਤ ਰੁਕ ਹੀ ਜਾਂਦਾ ਹੈ। ਤਦ ਉਹ ਬ੍ਰਹਿਮੰਡ ਇਕ ਦੂਜੇ ਵੱਲ ਆਉਣ ਲੱਗ ਜਾਂਦੇ ਹਨ ਅਤੇ ਧਰਤੀ ਸੁੰਗੜ ਜਾਂਦੀ ਹੈ। ਖ਼ਾਕਾ 3.2 ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਕਿ ਦੋ ਗੁਆਂਢੀ ਮੰਡਲਾਂ ਵਿਚਕਾਰਲਾ ਫ਼ਾਸਲਾ ਕਿਵੇਂ ਬਦਲਦਾ ਹੈ, ਜਿਉਂ-ਜਿਉਂ ਸਮਾਂ ਬੀਤਦਾ ਜਾਂਦਾ ਹੈ। ਇਹ ਸਿਫ਼ਰ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਵੱਧ ਤੋਂ ਵੱਧ ਹੱਦ ‘ਤੇ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮੁੜ ਘਟਦਾ-ਘਟਦਾ ਸਿਫ਼ਰ ਹੋ ਜਾਂਦਾ ਹੈ। ਦੂਜੀ ਕਿਸਮ ਦੀ ਪ੍ਰਾਪਤੀ ਅਨੁਸਾਰ, ਧਰਤੀ ਇਤਨੀ ਤੇਜ਼ੀ ਨਾਲ ਫੈਲ ਰਹੀ ਹੈ ਕਿ ਖਿੱਚ ਸ਼ਕਤੀ ਸਦਕਾ ਇਸ ਨੂੰ ਕਦੇ ਵੀ ਰੋਕ ਨਹੀਂ ਸਕਦੀ। ਹਾਂ ਇਸ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਕੁਝ ਮਠੇਰੀ ਜ਼ਰੂਰ ਕਰ ਸਕਦੀ ਹੈ। ਖ਼ਾਕਾ 3.3 ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਕਿ ਉਸ ਨਮੂਨੇ ਵਿਚਲੇ ਦੋ ਮੰਡਲਾਂ ਦੀ ਆਪਸੀ ਦੂਰੀ ਕਿਤਨੀ ਹੈ। ਇਹ ਸਿਫ਼ਰ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮੰਡਲ ਇਕ ਬੰਨ੍ਹਵੀਂ ਰਫ਼ਤਾਰ ਨਾਲ ਇਕ ਦੂਜੇ ਤੋਂ ਦੂਰ ਜਾ ਰਹੇ ਹਨ। ਹੁਣ ਲਉ ਤੀਜਾ ਗੁਰ। ਇਸ ਅਨੁਸਾਰ ਧਰਤੀ ਦਾ ਫੈਲਾਉ ਇਤਨੀ ਰਫ਼ਤਾਰ ਨਾਲ ਹੋ ਰਿਹਾ ਹੈ, ਜੋ ਧਰਤੀ ਨੂੰ ਢਹਿ-ਢੇਰੀ ਹੋਣ ਤੋਂ ਬਚਾਉਣ ਲਈ ਕਾਫ਼ੀ ਹੈ। ਇਸ ਹਾਲਤ ਵਿੱਚ, ਦੋ ਮੰਡਲਾਂ ਦਾ ਪਾੜਾ, ਖਾਕਾ 3.4 ਅਨੁਸਾਰ, ਸਿਫ਼ਰ ਤੋਂ ਹੀ ਸ਼ੁਰੂ ਹੁੰਦਾ ਹੈ ਅਤੇ ਸਦਾ ਹੀ ਜਾਰੀ ਰਹਿੰਦਾ ਹੈ। ਪਰੰਤੂ ਜਿਸ ਰਫ਼ਤਾਰ ਨਾਲ ਮੰਡਲ ਇਕ ਦੂਜੇ ਤੋਂ ਦੂਰ ਹੋ ਰਹੇ ਹਨ, ਉਹ ਘਟਦੀ ਤਾਂ ਰਹਿੰਦੀ ਹੈ, ਪਰ ਇਹ ਸਿਫ਼ਰ ਕਦੇ ਵੀ ਨਹੀਂ ਬਣੇਗੀ।

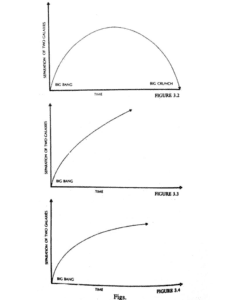
ਫਰਾਈਡਮੈਨ ਦੇ ਪਹਿਲੀ ਕਿਸਮ ਦੇ ਨਮੂਨੇ ਦਾ ਪ੍ਰਤੱਖ ਰੂਪ ਇਹ ਹੈ ਕਿ ਧਰਤੀ ਦੇ ਪੁਲਾੜ ਦਾ ਆਕਾਰ ਅਸੀਮ ਨਹੀਂ ਹੈ, ਪਰੰਤੂ ਇਸ ਦੇ ਪੁਲਾੜ ਦੇ ਦੁਆਲੇ ਕੋਈ ਦੀਵਾਰ ਨਹੀਂ ਹੈ। ਖਿੱਚ ਇਤਨੀ ਬਲਵਾਨ ਹੈ ਕਿ ਪੁਲਾੜ ਗੁਲਾਈ ਵਿੱਚ ਆਪਣੇ ਦੁਆਲੇ ਹੀ ਲਿਪਟ ਜਾਂਦਾ ਹੈ ਅਤੇ ਉਹ ਧਰਤੀ ਦੀ ਸਤਾਹ ਵਰਗਾ ਹੀ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ। ਜੇ ਕੋਈ ਵਿਅਕਤੀ ਧਰਤੀ ਦੀ ਸਤਾਹ ਉੱਤੇ ਕਿਸੇ ਵੀ ਇਕ ਪਾਸੇ ਤੁਰਦਾ ਜਾਵੇ, ਤਾਂ ਉਸ ਨੂੰ ਕਿਤੇ ਵੀ ਕੋਈ ਅਲੱਗ ਨਾਕਾ ਨਹੀਂ ਮਿਲੇਗਾ ਅਤੇ ਨਾ ਹੀ ਉਹ ਕਿਸੇ ਕੰਢੇ ਉੱਤੇ ਜਾ ਕੇ ਡਿੱਗ ਪਵੇਗਾ ਅਤੇ ਅੰਤ ਉਹ ਜਿੱਥੇ ਤੁਰਿਆ ਸੀ, ਮੁੜ ਕੇ ਉੱਥੇ ਹੀ ਪਹੁੰਚ ਜਾਵੇਗਾ। ਫਰਾਈਡਮੈਨ ਦੇ ਪਹਿਲੇ ਨਮੂਨੇ ਅਨੁਸਾਰ ਪੁਲਾੜ ਇਸ ਪ੍ਰਕਾਰ ਦਾ ਹੈ, ਪਰੰਤੂ ਇਸ ਦੀਆਂ ਤਿੰਨ ਦਿਸ਼ਾਵਾਂ ਹਨ, ਧਰਤੀ ਦੀ ਸਤਾਹ ਦੀਆਂ ਦੋ ਦਿਸ਼ਾਵਾਂ ਵਾਂਗ ਨਹੀਂ। ਚੌਥੀ ਦਿਸ਼ਾ ਸਮਾਂ ਹੈ ਅਤੇ ਉਹ ਵੀ ਸੀਮਤ ਹੈ, ਪਰੰਤੂ ਇਕ ਦੋ ਸਿਰਿਆਂ ਵਾਲੀ ਲਕੀਰ ਵਾਂਗ ਹੈ ਜਾਂ ਹੱਦਾਂ ਵਾਲੀ—ਇਕ ਸ਼ੁਰੂ ਵਾਲਾ ਅਤੇ ਇੱਕ ਅੰਤ ਵਾਲਾ। ਅਸੀਂ ਅੱਗੇ ਚੱਲ ਕੇ ਦੇਖਾਂਗੇ ਕਿ ਜਦੋਂ ਕੋਈ ਆਮ ਅਨੁਪਾਤ ਨੂੰ (Quantum mechanics) ਦੇ ਭਰੋਸਾਹੀਣ ਅਸੂਲ ਨਾਲ ਜੋੜੇਗਾ, ਤਾਂ ਪੁਲਾੜ ਅਤੇ ਸਮੇਂ ਦੋਹਾਂ ਦਾ ਕੰਢਿਆਂ ਅਤੇ ਦੀਵਾਰਾਂ ਤੋਂ ਬਿਨਾਂ ਸੀਮਤ ਹੋਣਾ ਲੱਭੇਗਾ। ਇਹ ਵਿਚਾਰ ਕਿ ਕੋਈ ਧਰਤੀ ਦਾ ਚੱਕਰ ਲਾਉਣ ਉਪਰੰਤ ਜਿੱਥੋਂ ਚੱਲਿਆ ਸੀ, ਉੱਥੇ ਹੀ ਮੁੜ ਆਉਂਦਾ ਹੈ, ਇਕ ਵਿਗਿਆਨਕ ਫੁਰਨਾ ਹੈ, ਪਰੰਤੂ ਇਸ ਉੱਤੇ ਅਮਲ ਕਰਨ ਵਾਲੀ ਗੱਲ ਮਹੱਤਤਾ ਨਹੀਂ ਰੱਖਦੀ ਕਿਉਂਕਿ ਇਹ ਤਾਂ ਪਤਾ ਲਾਇਆ ਹੀ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਚੱਕਰ ਪੂਰਾ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਢਹਿ-ਢੇਰੀ ਹੋ ਜਾਵੇਗੀ ਅਤੇ ਸਿਫ਼ਰ ਦੇ ਬਰਾਬਰ ਹੋ ਜਾਵੇਗੀ। ਤੁਹਾਨੂੰ ਉਸੇ ਥਾਂ ਮੁੜ ਕੇ ਆਉਣ ਲਈ, ਜਿੱਥੋਂ ਤੁਸੀਂ ਚੱਲੇ ਸੀ। ਧਰਤੀ ਦਾ ਖ਼ਾਤਮਾ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਚੱਕਰ ਲਾਉਣ ਲਈ, ਰੌਸ਼ਨੀ ਦੀ ਰਫ਼ਤਾਰ ਨਾਲੋਂ ਤੇਜ਼ ਰਫ਼ਤਾਰ ਨਾਲ ਚੱਲਣ ਦੀ ਲੋੜ ਪਵੇਗੀ ਅਤੇ ਇਸ ਗੱਲ ਦੀ ਆਗਿਆ ਨਹੀਂ ਮਿਲ ਸਕਦੀ ।

ਫਰਾਈਡਮੈਨ ਦੇ ਪਹਿਲੇ ਨਮੂਨੇ ਅਨੁਸਾਰ ਪੁਲਾੜ ਜੋ ਫੈਲਦਾ ਹੈ ਅਤੇ ਫੇਰ ਢਹਿ- ਢੇਰੀ ਹੋ ਜਾਂਦਾ ਹੈ, ਆਪਣੇ ਆਪ ਹੀ ਇਕੱਠਾ ਹੋ ਜਾਂਦਾ ਹੈ, ਜਿਵੇਂ ਧਰਤੀ ਦੀ ਸਤਾਹ ਹੁੰਦੀ ਹੈ। ਇਸ ਲਈ ਪੁਲਾੜ ਆਕਾਰ ਵਿੱਚ ਅਸੀਮਿਤ ਹੈ। ਦੂਜੀ ਕਿਸਮ ਦੇ ਨਮੂਨੇ ਅਨੁਸਾਰ, ਪੁਲਾੜ ਸਦਾ ਹੀ ਫੈਲਦਾ ਰਹਿੰਦਾ ਹੈ, ਇਹ ਦੂਜੇ ਪਾਸੇ ਨੂੰ ਮੁੜ ਜਾਂਦਾਹੈ, ਜਿਸ ਪ੍ਰਕਾਰ ਕਾਠੀ ਮੁੜ ਜਾਂਦੀ ਹੈ। ਇਸ ਲਈ ਇਸ ਹਾਲਤ ਵਿੱਚ ਵੀ ਪੁਲਾੜ ਅਸੀਮਤ ਹੈ। ਆਖ਼ਰ ਫਰਾਈਡਮੈਨ ਦੇ ਤੀਜੇ ਨਮੂਨੇ ਅਨੁਸਾਰ ਪੁਲਾੜ, ਇਕ ਨਿਸ਼ਚਿਤ ਰਫ਼ਤਾਰ ਨਾਲ ਫੈਲਦਾ ਹੈ, ਪੁਲਾੜ ਪੱਧਰਾ ਹੈ (ਅਤੇ ਇਸ ਲਈ ਸੀਮਤ ਵੀ ਹੈ।) ਪਰੰਤੂ ਫਰਾਈਡਮੈਨ ਦਾ ਕਿਹੜਾ ਨਮੂਨਾ ਧਰਤੀ ਦੀ ਵਿਆਖਿਆ ਕਰਦਾ ਹੈ ? ਕੀ ਧਰਤੀ ਕਦੇ ਫੈਲਣੋਂ ਰੁਕ ਜਾਵੇਗੀ ਅਤੇ ਸੁੰਗੜਨ ਲੱਗ ਜਾਵੇਗੀ ਜਾਂ ਕੀ ਇਹ ਸਦਾ ਫੈਲਦੀ ਹੀ ਰਹੇਗੀ ? ਇਸ ਪ੍ਰਸ਼ਨ ਦਾ ਉੱਤਰ ਦੇਣ ਲਈ, ਸਾਨੂੰ ਧਰਤੀ ਦੀ ਫੈਲਣ ਦੀ ਮੌਜੂਦਾ ਰਫ਼ਤਾਰ ਦਾ ਪਤਾ ਲਗਾਉਣ ਦੀ ਲੋੜ ਹੈ ਅਤੇ ਇਸ ਦੀ ਮੌਜੂਦਾ ਸੰਘਣੇਪਣ ਦੀ ਔਸਤ ਦਾ ਪਤਾ ਕਰਨਾ ਪਵੇਗਾ। ਜੇ ਸੰਘਣਾਪਣ ਇਕ ਖ਼ਾਸ ਮਾਤਰਾ ਨਾਲੋਂ ਘੱਟ ਹੈ, ਜਿਹੜੀ ਮਾਤਰਾ ਦਾ ਆਧਾਰ ਫੈਲਣ ਦੀ ਰਫ਼ਤਾਰ ਹੈ, ਤਾਂ ਖਿੱਚ ਸ਼ਕਤੀ ਬਹੁਤ ਹੀ ਕਮਜ਼ੋਰ ਹੋਵੇਗੀ ਅਤੇ ਫੈਲਾਉ ਦੇ ਅਮਲ ਨੂੰ ਰੋਕ ਨਹੀਂ ਸਕੇਗੀ। ਜੇ ਸੰਘਣਾਪਣ ਉਸ ਨਿਸ਼ਚਿਤ ਮਾਤਰਾ ਨਾਲੋਂ ਵਧੇਰੇ ਹੋਵੇ, ਤਾਂ ਖਿੱਚ-ਸ਼ਕਤੀ ਭਵਿੱਖ ਵਿੱਚ ਕਿਸੇ ਸਮੇਂ ਫੈਲਾਉ ਦੇ ਅਮਲ ਨੂੰ ਰੋਕ ਦੇਵੇਗੀ ਅਤੇ ਧਰਤੀ ਦੇ ਢਹਿ-ਢੇਰੀ ਹੋ ਜਾਣ ਦਾ ਕਾਰਨ ਬਣ ਜਾਵੇਗੀ।

ਅਸੀਂ ਫੈਲਾਓ ਦੀ ਮੌਜੂਦਾ ਰਫ਼ਤਾਰ ਦਾ ਨਿਰਣਾ ਦੂਜੇ ਖੰਡਾਂ ਦੀ ਸਾਥੋਂ ਦੂਰ ਜਾਣ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਨਾਪ ਕੇ ਹੀ ਕਰ ਸਕਦੇ ਹਾਂ ਅਤੇ ਅਜਿਹਾ ਡੋਪਲਰ (Doppler) ਦੀ ਵਰਤੋਂ ਨਾਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਇਹ ਨਿਰਣਾ ਸਹੀ ਸਹੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਪਰੰਤੂ ਖੰਡਾਂ ਦੀਆਂ ਦੂਰੀਆਂ ਦਾ ਪੂਰਾ ਪਤਾ ਨਹੀਂ ਹੈ, ਕਿਉਂਕਿ ਅਸੀਂ ਉਨ੍ਹਾਂ ਦੂਰੀਆਂ ਨੂੰ ਅਸਿੱਧੇ ਤਰੀਕੇ ਨਾਲ ਮਿਣ ਸਕਦੇ ਹਾਂ। ਅਸੀਂ ਕੇਵਲ ਇਹੋ ਜਾਣਦੇ ਹਾਂ ਕਿ ਧਰਤੀ ਕਈ ਅਰਬ ਯੁਗਾਂ ਵਿੱਚ 5 ਤੋਂ ਲੈ ਕੇ 10 ਪ੍ਰਤੀਸ਼ਤ ਦੀ ਦਰ ਨਾਲ ਹੀ ਫੈਲਦੀ ਹੈ। ਪਰੰਤੂ ਧਰਤੀ ਦੇ ਔਸਤ ਸੰਘਣੇਪਣ ਪ੍ਰਤੀ ਸਾਡਾ ਭੁਲੇਖਾ ਹੋਰ ਵੀ ਵਧੇਰੇ ਹੈ। ਜੇ ਅਸੀਂ ਆਪਣੇ ਅਤੇ ਹੋਰ ਖੰਡਾਂ ਵਿਚਲੇ ਨਜ਼ਰ ਆ ਰਹੇ ਤਾਰਿਆਂ ਦੇ ਆਕਾਰਾਂ ਨੂੰ ਜੋੜ ਲਈਏ ਤਾਂ ਵੀ ਇਹ ਜੋੜ ਧਰਤੀ ਦੇ ਫੈਲਾਓ ਨੂੰ ਰੋਕਣ ਲਈ ਲੋੜੀਂਦੀ ਮਾਤਰਾ ਦਾ ਇਕ ਸੌਵਾਂ ਹਿੱਸਾ ਹੀ ਹੋਵੇਗਾ ਅਤੇ ਅਜਿਹਾ ਵੀ ਫੈਲਾਓ ਦੀ ਘਾਟ ਤੋਂ ਘੱਟ ਗਤੀ ਵਾਲਾ ਪਦਾਰਥ ਬਹੁਤ ਵੱਡੀ ਮਾਤਰਾ ਵਿੱਚ ਹੋ ਸਕਦਾ ਹੈ, ਜਿਸ ਨੂੰ ਅਸੀਂ ਸਿੱਧੇ ਤੌਰ ‘ਤੇ ਦੇਖ ਨਹੀਂ ਸਕਦੇ। ਪਰੰਤੂ ਸਾਨੂੰ ਪਤਾ ਹੈ ਕਿ ਅਜਿਹਾ ਪਦਾਰਥ ਮੌਜੂਦ ਹੈ, ਕਿਉਂਕਿ ਖੰਡਾਂ ਵਿਚਲੇ ਤਾਰਿਆਂ ਦੇ ਚੱਕਰਾਂ ਉੱਤੇ ਖਿੱਚ ਦਾ ਪ੍ਰਭਾਵ ਪ੍ਰਤੱਖ ਪੈਂਦਾ ਹੈ। ਫੇਰ, ਬਹੁਤ ਸਾਰੇ ਖੰਡ ਤਾਂ ਗੁੱਛਿਆਂ ਵਿੱਚ ਹੀ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ, ਇਸ ਲਈ ਖੰਡਾਂ ਦੇ ਗੁੱਛਿਆਂ ਵਿਚਕਾਰ ਕਾਲਾ ਪਦਾਰਥ ਮੌਜੂਦ ਹੋਣਾ ਸੰਭਵ ਹੈ, ਕਿਉਂਕਿ ਇਨ੍ਹਾਂ ਦਾ ਖੰਡਾਂ ਦੀ ਗਤੀ ਉੱਤੇ ਅਸਰ ਪੈਂਦਾ ਰਹਿੰਦਾ ਹੈ, ਤਾਂ ਵੀ ਇਹ ਜੋੜ ਧਰਤੀ ਦੇ ਫੈਲਾਓ ਨੂੰ ਰੋਕਣ ਵਾਲੀ ਮਾਤਰਾ ਦਾ ਦਸਵਾਂ ਹਿੱਸਾ ਹੀ ਬਣਦਾ ਹੈ। ਪਰੰਤੂ ਕਿਸੇ ਵੱਖਰੇ ਪਦਾਰਥ ਦੇ ਮੌਜੂਦ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਤੋਂ ਇਨਕਾਰ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ, ਜਿਹੜਾ ਸਾਰੀ ਧਰਤੀ ਵਿੱਚ ਤਕਰੀਬਨ ਇਕੋ ਜਿਹੀ ਮਾਤਰਾ ਵਿੱਚ ਫੈਲਿਆ ਹੋਵੇ, ਜਿਸ ਨੂੰ ਹਾਲੇ ਤੱਕ ਅਸੀਂ ਦੇਖ ਨਹੀਂ ਸਕੇ ਅਤੇ ਜਿਸ ਨਾਲ ਧਰਤੀ ਦੇ ਫੈਲਾਓ ਨੂੰ ਰੋਕਣ ਲਈ ਸੰਘਣੇਪਣ ਦੇ ਔਸਤ ਸੰਘਣੇਪਣ ਵਿੱਚ ਵਾਧਾ ਹੋ ਸਕਦਾ ਹੋਵੇ। ਸਾਡੀ ਮੌਜੂਦਾ ਜਾਣਕਾਰੀ ਤੋਂ ਸੰਕੇਤ ਮਿਲਦਾ ਹੈ ਕਿ ਧਰਤੀ ਸਦਾ ਫੈਲਦੀ ਰਹੇਗੀ, ਪਰੰਤੂ ਸਾਡਾ ਵਿਸ਼ਵਾਸ ਹੈ ਕਿ ਧਰਤੀ ਦਾ ਖ਼ਾਤਮਾ ਹਾਲੇ ਦਸ ਅਰਬ ਸਾਲ ਤੋਂ ਪਹਿਲਾਂ ਨਹੀਂ ਹੋ ਸਕਦਾ ਕਿਉਂਕਿ ਇਤਨੇ ਲੰਮੇ ਸਮੇਂ ਤੋਂ ਇਹ ਪਹਿਲਾਂ ਫੈਲਦੀ ਰਹੀ ਹੈ। ਸਾਨੂੰ ਕੋਈ ਚਿੰਤਾ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ। ਉਸ ਵੇਲੇ ਤੱਕ, ਜੇ ਅਸੀਂ ਆਪਣੇ ਸੂਰਜ ਖੰਡ ਤੋਂ ਬਾਹਰ ਜਾ ਕੇ ਆਬਾਦ ਨਾ ਹੋਏ ਤਾਂ ਮਨੁੱਖ ਮਾਤਰ ਚਿਰੋਕਣਾ ਮਰ ਮਿਟ ਚੁੱਕਾ ਹੋਵੇਗਾ ਅਤੇ ਸਾਡੇ ਸੂਰਜ ਦਾ ਵੀ ਖ਼ਾਤਮਾ ਹੋ ਚੁੱਕਾ ਹੋਵੇਗਾ। ਫਰਾਈਡਮੈਨ ਦੇ ਫ਼ੈਸਲਿਆਂ ਤੋਂ ਇਹ ਗੱਲ ਸਪੱਸ਼ਟ ਹੋ ਗਈ ਹੈ ਕਿ ਕੋਈ ਦਸ ਤੋਂ ਵੀਹ ਅਰਬ ਸਾਲ ਪਹਿਲਾਂ, ਕਿਸੇ ਬੀਤੇ ਸਮੇਂ ਵਿੱਚ ਖੰਡਾਂ ਵਿਚਲੀ ਵਿੱਥ ਸਿਫ਼ਰ ਦੇ ਬਰਾਬਰ ਹੋਵੇਗੀ। ਉਸ ਵੇਲੇ, ਜਿਸ ਨੂੰ ਅਸੀਂ ਮਹਾਨ ਧਮਾਕਾ (Big Bang) ਕਹਿੰਦੇ ਹਾਂ, , ਧਰਤੀ ਦਾ ਸੰਘਣਾਪਣ ਅਤੇ ਪੁਲਾੜੀ ਸਮੇਂ ਦੀ ਰੇਖਾ ਅਸੀਮਤ ਹੋਵੇਗੀ, ਕਿਉਂਕਿ ਗਣਿਤ-ਵਿੱਦਿਆ ਅਸੀਮਤ ਨੰਬਰਾਂ ਨੂੰ ਸਮਝ ਹੀ ਨਹੀਂ ਸਕਦੀ। ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਮਾਤਰਾ ਦਾ ਆਮ ਸਿਧਾਂਤ (ਜੋ ਫਰਾਈਡਮੈਨ ਦੇ ਫ਼ੈਸਲਿਆਂ ਦਾ ਆਧਾਰ ਹੈ), ਜ਼ਾਹਰ ਕਰਦਾ ਹੈ ਕਿ ਧਰਤੀ ਵਿੱਚ ਕੋਈ ਅਜਿਹਾ ਨੁਕਤਾ ਹੈ, ਜਿੱਥੇ ਇਸ ਸਿਧਾਂਤ ਦਾ ਖੰਡਨ ਹੋ ਜਾਂਦਾ ਹੈ। ਅਜਿਹੇ ਨੁਕਤੇ ਦੀ ਮਿਸਾਲ ਰਿਆਜ਼ ਦੇ ਨਾਂ ਅਨੁਸਾਰ ਇਸ ਦੀ ਵਿਲੱਖਣਤਾ ਹੈ। ਅਸਲ ਵਿੱਚ ਸਾਡੇ ਸਾਰੇ ਵਿਗਿਆਨਿਕ ਸਿਧਾਂਤ ਇਹ ਸੋਚ ਕੇ ਘੜੇ ਗਏ ਹਨ ਕਿ ਪੁਲਾੜੀ ਸਮੇਂ ਦੇ ਰੂਪ ਸਾਵੇਂ ਪੱਧਰੇ ਹਨ ਅਤੇ ਤਕਰੀਬਨ ਚਪਟੇ ਹਨ, ਇਸ ਲਈ ਮਹਾਨ ਧਮਾਕੇ ਦੇ ਅਨੂਠੇ ਸਮੇਂ ਟੁੱਟ-ਫੁੱਟ ਗਏ ਸਨ। ਜਦੋਂ ਪੁਲਾੜੀ ਸਮੇਂ ਦੀ ਟੇਢੀ ਰੇਖਾ ਦੀ ਕੋਈ ਸੀਮਾ ਨਹੀਂ ਸੀ। ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਭਾਵੇਂ ਕੁਝ ਘਟਨਾਵਾਂ ਮਹਾਨ ਧਮਾਕੇ ਤੋਂ ਪਹਿਲਾਂ ਵਾਪਰੀਆਂ ਵੀ ਹੋਣਗੀਆਂ, ਉਨ੍ਹਾਂ ਘਟਨਾਵਾਂ ਨੂੰ ਉਸ ਤੋਂ ਉਪਰੰਤ ਵਾਪਰਨ ਵਾਲੀਆਂ ਘਟਨਾਵਾਂ ਦਾ ਨਿਰਣਾ ਕਰਨ ਲਈ ਵਰਤਿਆ ਨਹੀਂ ਜਾ ਸਕਦਾ, ਕਿਉਂਕਿ ਭਵਿੱਖਬਾਣੀ ਮਹਾਨ ਧਮਾਕੇ ਵੇਲੇ ਮੁਕ ਮੁਕਾ ਗਈ ਹੋਵੇਗੀ। ਇਸ ਦੇ ਟਾਕਰੇ ਵਿੱਚ, ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਧਮਾਕੇ ਮਗਰੋਂ ਕੀ ਕੁਝ ਵਾਪਰ ਚੁੱਕਾ ਹੈ, ਅਸੀਂ ਇਹ ਨਿਰਣਾ ਕਰ ਹੀ ਨਹੀਂ ਸਕਦੇ ਕਿ ਮਹਾਨ ਧਮਾਕੇ ਤੋਂ ਪਹਿਲਾਂ ਕੀ ਕੁਝ ਵਾਪਰ ਚੁੱਕਾ ਸੀ। ਜਿੱਥੋਂ ਤੱਕ ਸਾਡਾ ਸੰਬੰਧ ਹੈ, ਮਹਾਨ ਧਮਾਕੇ ਤੋਂ ਪਹਿਲਾਂ ਵਾਪਰਨ ਵਾਲੀਆਂ ਘਟਨਾਵਾਂ ਦਾ ਕੋਈ ਅਰਥ ਹੀ ਨਹੀਂ ਹੈ। ਇਸ ਲਈ ਧਰਤੀ ਦੇ ਵਿਗਿਆਨਿਕ ਲੇਖੇ-ਜੋਖੇ ਦਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਆਧਾਰ ਨਹੀਂ ਬਣਾਇਆ ਜਾ ਸਕਦਾ। ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਉੱਤੇ ਲਕੀਰ ਫੇਰ ਦੇਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਕਹਿਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਸਮੇਂ ਦਾ ਅਰੰਭ ਮਹਾਨ ਧਮਾਕੇ ਤੋਂ ਹੀ ਹੋਇਆ ਹੈ। ਕੁਝ ਲੋਕ ਇਹ ਗੱਲ ਮੰਨਣ ਨੂੰ ਤਿਆਰ ਨਹੀਂ ਹਨ ਕਿ ਸਮੇਂ ਦਾ ਵੀ ਕੋਈ ਅਰੰਭ ਸੀ। ਸ਼ਾਇਦ ਇਸ ਲਈ ਕਿ ਅਜਿਹਾ ਮੰਨਣ ਨਾਲ ਈਸ਼ਵਰੀ ਅਮਲ ਦੀ ਬੇਅਦਬੀ ਹੁੰਦੀ ਹੈ, ਜਾਂ ਉਸ ਦੀ ਅਵੱਗਿਆ ਹੁੰਦੀ ਹੈ। (ਦੂਜੇ ਬੰਨ੍ਹੇ ਕੈਥੋਲਿਕ ਧਰਮ ਨੇ ਮਹਾਨ ਧਮਾਕੇ ਨੂੰ ਹੀ ਆਧਾਰ ਮੰਨ ਲਿਆ ਹੈ ਅਤੇ 1951 ਈਸਵੀ ਵਿੱਚ ਇਸ ਵਿਚਾਰ ਨੂੰ ਬਾਈਬਲ ਦੇ ਅਨੁਕੂਲ ਦੱਸਿਆ ਹੈ।) ਕਈ ਵਾਰ ਇਸ ਨਤੀਜੇ ਤੋਂ ਬਚਣ ਲਈ ਕੋਸ਼ਿਸ਼ਾਂ ਹੁੰਦੀਆਂ ਹਨ ਕਿ ਕਦੇ ਮਹਾਨ ਧਮਾਕਾ ਹੋਇਆ ਸੀ। ਜਿਸ ਵਿਚਾਰਧਾਰਾ ਨੂੰ ਸਭ ਤੋਂ ਵੱਧ ਸਮਰਥਨ ਮਿਲਿਆ, ਉਹ ਟਿਕਵੀਂ ਹਾਲਤ ਦਾ ਵਿਚਾਰ ਸੀ। 1948 ਵਿੱਚ ਨਾਜ਼ੀ ਕਬਜ਼ੇ ਅਧੀਨ ਆਸਟਰੀਆ ਤੋਂ ਆਏ ਹੋਏ ਦੋ ਸ਼ਰਨਾਰਥੀਆਂ ਹਰਮਨ ਬੌਡੀ (Hermann Bondi) ਅਤੇ ਥਾਮਸ ਗੋਲਡ ਨੇ ਅਤੇ ਬਰਤਾਨੀਆ ਦੇ ਫਰੈਡ ਹੋਇਲ (Fred Hoyle) ਨਾਲ ਮਿਲ ਕੇ, ਜਿਹੜਾ ਜੰਗ ਦੌਰਾਨ ਰਾਡਾਰ ਦੇ ਵਿਕਾਸ ਲਈ ਉਸ ਦੇ ਨਾਲ ਕੰਮ ਕਰਦਾ ਰਿਹਾ ਸੀ, ਇਹ ਵਿਚਾਰ ਪੇਸ਼ ਕੀਤਾ ਸੀ। ਖ਼ਿਆਲ ਇਹ ਸੀ ਕਿ ਕਿਉਂਕਿ ਖੰਡ ਇਕ ਦੂਜੇ ਕੋਲੋਂ ਦੂਰ ਜਾਂਦੇ ਰਹਿੰਦੇ ਹਨ। ਉਨ੍ਹਾਂ ਦੇ ਵਿਚਕਾਰ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ‘ਤੇ ਨਵੇਂ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਪਦਾਰਥ ਤੋਂ ਲਗਾਤਾਰ ਨਵੇਂ ਖੰਡ ਪੈਦਾ ਹੁੰਦੇ ਰਹਿੰਦੇ ਹਨ। ਇਸ ਲਈ ਧਰਤੀ ਹਰ ਸਮੇਂ ਅਤੇ ਪੁਲਾੜ ਦੇ ਹਰ ਇਕ ਹਿੱਸੇ ਵਿੱਚ, ਲਗਭਗ ਪਹਿਲਾਂ ਵਰਗੀ ਇਕੋ ਜਿਹੀ ਲੱਗਦੀ ਰਹੇਗੀ। ਟਿਕਵੀਂ ਹਾਲਤ ਵਾਲੇ ਵਿਚਾਰ ਸਦਕਾ ਅਨੁਪਾਤ ਦੇ ਸਾਧਾਰਣ ਸਿਧਾਂਤ ਵਿੱਚ ਇਸ ਲਈ ਸੋਧ ਕਰਨੀ ਪੈ ਗਈ ਕਿ ਨਵਾਂ ਪਦਾਰਥ ਲਗਾਤਾਰ ਪੈਦਾ ਹੁੰਦਾ ਰਹੇ, ਪਰੰਤੂ ਇਸ ਦੀ ਰਫ਼ਤਾਰ ਇਸ ਕਦਰ ਮਠੇਰੀ ਸੀ (ਇਕ ਟੁਕੜਾ ਇਕ ਕਿਊਬਿਕ ਕਿਲੋਮੀਟਰ ਪ੍ਰਤੀ ਸਾਲ) ਕਿ ਤਜਰਬੇ ਕਰਨ ਉੱਤੇ ਇਸ ਦਾ ਕੋਈ ਅਸਰ ਨਹੀਂ ਸੀ ਪੈਂਦਾ। ਇਹ ਵਿਚਾਰ ਵਿਗਿਆਨਿਕ ਵਿਚਾਰ ਜ਼ਰੂਰ ਸੀ, ਜਿਸ ਦਾ ਜ਼ਿਕਰ ਕਾਂਡ 1 ਵਿੱਚ ਕੀਤਾ ਜਾ ਚੁੱਕਾ ਹੈ। ਇਹ ਇਕ ਸਾਧਾਰਣ ਵਿਚਾਰ ਸੀ ਅਤੇ ਸਪੱਸ਼ਟ ਆਧਾਰ ਪ੍ਰਗਟ ਕਰਦਾ ਸੀ, ਜਿਨ੍ਹਾਂ ਦੀ ਪਰਖ ਦੇਖਣ ਨਾਲ ਹੀ ਕੀਤੀ ਜਾ ਸਕਦੀ ਸੀ। ਇਕ ਆਧਾਰ ਇਹ ਸੀ ਉਨ੍ਹਾਂ ਖੰਡਾਂ ਦੀ ਜਾਂ ਪੁਲਾੜ ਦੇ ਕਿਸੇ ਇਕ ਹਿੱਸੇ ਵਿਚਲੇ ਧਰਤੀ ਉੱਤੇ ਇਕੋ ਜਿਹੀਆਂ ਵਸਤਾਂ ਹਰ ਸਮੇਂ ਅਤੇ ਹਰ ਥਾਂ ਦੇਖਣ ਵਿੱਚ ਪਹਿਲਾਂ ਜਿਤਨੇ ਹੀ ਨਜ਼ਰ ਆਉਣੇ ਚਾਹੀਦੇ ਹਨ। 1950 ਈਸਵੀ ਦੇ ਅੰਤ ਵਿੱਚ ਅਤੇ 1960 ਈਸਵੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ, ਕੈਂਬਰਿਜ ਵਿਖੇ ਨਜੂਮੀਆਂ ਦੇ ਇਕ ਦਲ ਨੇ ਮਾਰਟਿਨ ਰਾਈਲ ਦੀ ਅਗਵਾਈ ਵਿੱਚ, ਜਿਹੜਾ ਬੌਡੀ, ਗੋਲਡ ਅਤੇ ਹੋਇਲ ਨਾਲ ਜੰਗ ਦੇ ਦੌਰਾਨ ਰਾਡਾਰ ਦੇ ਵਿਕਾਸ ਵਿੱਚ ਕੰਮ ਕਰਦਾ ਰਿਹਾ ਸੀ) ਬਾਹਰਲੇ ਪੁਲਾੜ ਤੋਂ ਆਉਣ ਵਾਲੀਆਂ ਲਹਿਰਾਂ ਦੇ ਸਰੋਤ ਦੀ ਪੜਤਾਲ ਕੀਤੀ ਸੀ। ਕੈਂਬਰਿਜ ਦੇ ਦਲ ਨੇ ਪ੍ਰਗਟ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਰੇਡੀਓ ਦੇ ਇਹ ਸੋਮੇ ਸਾਡੇ ਮੰਡਲ ਤੋਂ ਬਾਹਰ ਮੌਜੂਦ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ। (ਸੱਚਮੁੱਚ ਉਨ੍ਹਾਂ, ਵਿੱਚੋਂ ਬਹੁਤੇ ਮੰਡਲ ਦੂਜੇ ਮੰਡਲਾਂ ਨਾਲ ਜੁੜੇ ਹੋਏ ਸਨ।) ਅਤੇ ਇਹ ਵੀ ਜ਼ਾਹਰ ਕੀਤਾ ਸੀ, ਕਿ ਬਲਵਾਨ ਸੋਮਿਆਂ ਨਾਲ ਨਿਰਬਲ ਸੋਮੇ ਬਹੁਤ ਹਨ। ਉਨ੍ਹਾਂ ਅਨੁਸਾਰ ਜ਼ਿਆਦਾ ਦੁਰੇਡੇ ਸੋਮੇ ਨਿਰਬਲ ਸਨ ਅਤੇ ਬਲਵਾਨ ਸੋਮੇ ਨੇੜੇ ਵਾਲੇ ਸਨ । ਨੇੜਲੇ ਸੋਮਿਆਂ ਲਈ ਪੁਲਾੜ ਵਿੱਚ ਸੋਮੇ ਬਹੁਤ ਘੱਟ ਸਨ ਅਤੇ ਦੁਰੇਡੇ ਸੋਮਿਆਂ ਲਈ ਬਹੁਤੇ ਸਨ। ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਅਸੀਂ ਇਕ ਮਹਾਨ ਖਿੱਤੇ ਦੇ ਕੇਂਦਰ ਵਿੱਚ ਵਿਚਰ ਰਹੇ ਹਾਂ, ਜਿੱਥੇ ਹੋਰ ਥਾਂਵਾਂ ਨਾਲੋਂ ਸੋਮੇ ਬਹੁਤ ਘੱਟ ਹਨ। ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਭੂਤਕਾਲ ਵਿੱਚ, ਜਦੋਂ ਰੇਡੀਓ ਲਹਿਰਾਂ ਨੇ ਸਾਡੇ ਵੱਲ ਚਾਲੇ ਪਾਏ ਸਨ, ਗਿਣਤੀ ਵਿੱਚ ਹੁਣ ਦੇ ਟਾਕਰੇ ਵਿੱਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਸਨ । ਹਰ ਇਕ ਵਿਆਖਿਆ ਨਾਲ ਟਿਕਵੀਂ ਹਾਲਤ ਵਾਲੇ ਵਿਚਾਰ ਦੇ ਆਧਾਰਾਂ ਦੀ ਵਿਰੋਧਤਾ ਹੁੰਦੀ ਹੈ। ਉੱਪਰੋਂ, 1965 ਵਿੱਚ ਪੈਨਜ਼ੀਆ (Penzia) ਅਤੇ ਵਿਲਸਨ ਵੱਲੋਂ ਕੀਤੀ ਹੋਈ ਮਾਈਕਰੋ ਵੇਵ ਲਹਿਰਾਂ ਦੀ ਰੇਡੀਏਸ਼ਨ ਦੀ ਖੋਜ ਨੇ ਪ੍ਰਗਟ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਭੂਤਕਾਲ ਵਿੱਚ, ਧਰਤੀ ਵਧੇਰੇ ਸੰਘਣੀ ਸੀ। ਇਸ ਲਈ ਟਿਕਵੇਂ ਆਧਾਰ ਦਾ ਤਿਆਗ ਕਰਨਾ ਪੈ ਗਿਆ।

1963 ਵਿੱਚ ਦੋ ਰੂਸੀ ਵਿਗਿਆਨਿਕਾਂ ਐਵਜਨਾਈ ਲਿਟਸੇ (Evgenii Lifshitz) ਅਤੇ ਇਜ਼ਾਕ ਖਲਮੀਕੋਵ (Asaac Khalamikov) ਨੇ ਇਕ ਹੋਰ ਕੋਸ਼ਿਸ਼ ਇਹ ਸਾਬਤ ਕਰਨ ਲਈ ਕੀਤੀ ਸੀ ਕਿ ਮਹਾਨ ਧਮਾਕੇ ਦੀ ਘਟਨਾ ਸਵੀਕਾਰੀ ਨਾ ਜਾਵੇ ਅਤੇ ਨਾ ਹੀ ਸਮੇਂ ਦਾ ਅਰੰਭ ਮੰਨਣਾ ਪਵੇ। ਉਨ੍ਹਾਂ ਨੇ ਦਲੀਲ ਦਿੱਤੀ ਸੀ ਕਿ ਮਹਾਨ ਧਮਾਕਾ ਫਰਾਈਡਮੈਨ ਇਕੱਲੇ ਦਾ ਇਕ ਫੁਰਨਾ ਹੋ ਸਕਦਾ ਹੈ, ਜਿਹੜਾ ਧਰਤੀ ਦੀ ਅਸਲੀਅਤ ਦਾ ਅੰਦਾਜ਼ਾ ਹੀ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ। ਸ਼ਾਇਦ ਸਾਰੇ ਫੁਰਨਿਆਂ ਵਿੱਚੋਂ, ਫਰਾਈਡਮੈਨ ਦਾ ਫੁਰਨਾ ਹੀ ਮਹਾਨ ਧਮਾਕੇ ਦੀ ਵਿਲੱਖਣਤਾ ਵਾਲਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਤੋਂ ਧਰਤੀ ਦੀ ਅਸਲੀਅਤ ਦਾ ਅੰਦਾਜ਼ਾ ਲਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਫਰਾਈਡਮੈਨ ਦੇ ਫੁਰਨੇ ਅਨੁਸਾਰ, ਮੰਡਲ ਸਮੂਹਕ ਤੌਰ ‘ਤੇ ਇਕ ਦੂਜੇ ਤੋਂ ਦੂਰ ਜਾ ਰਹੇ ਹਨ। ਫੇਰ ਇਹ ਕੋਈ ਹੈਰਾਨੀ ਵਾਲੀ ਗੱਲ ਨਹੀਂ ਹੈ ਕਿ ਕਿਸੇ ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿੱਚ, ਇਹ ਸਾਰੇ ਮੰਡਲ ਇਕੋ ਥਾਂ ਮੌਜੂਦ ਹੋਣ।

ਪਰੰਤੂ, ਅਸਲੀ ਬ੍ਰਹਿਮੰਡ ਉੱਤੇ, ਇਹ ਮੰਡਲ ਇਕ ਦੂਜੇ ਤੋਂ ਸਿੱਧੀਆਂ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚ ਦੂਰ ਨਹੀਂ ਜਾ ਰਹੇ, ਸਗੋਂ ਆਸੇ-ਪਾਸੇ ਹੀ ਚਲੇ ਜਾਂਦੇ ਹਨ। ਇਸ ਲਈ ਵਾਸਤਵ ਵਿੱਚ, ਉਨ੍ਹਾਂ ਦੇ ਇਕੋ ਥਾਂ ਮੌਜੂਦ ਹੋਣ ਦੀ ਲੋੜ ਨਹੀਂ ਸੀ। ਹਾਂ ਉਹ ਇਕ ਦੂਜੇ ਦੇ ਨੇੜੇ ਜ਼ਰੂਰ ਹੋਣਗੇ। ਫੇਰ ਤਾਂ ਸਾਡੀ ਅਜੋਕੀ ਫੈਲਣ ਵਾਲੀ ਸ੍ਰਿਸ਼ਟੀ ਮਹਾਨ ਧਮਾਕੇ ਦਾ ਨਤੀਜਾ ਨਹੀਂ ਹੈ, ਸਗੋਂ ਕਿਸੇ ਪਹਿਲੇ ਸੁੰਗੜ ਰਹੇ ਪੜਾਅ ਵਿੱਚੋਂ ਪੈਦਾ ਹੋਈ ਹੈ, ਕਿਉਂਕਿ ਬ੍ਰਹਿਮੰਡ ਨੇ ਆਪਣੇ ਟੁਕੜੇ ਬਖੇਰ ਦਿੱਤੇ ਹੋਣਗੇ, ਜਿਹੜੇ ਇਕ ਦੂਜੇ ਨਾਲ ਟਕਰਾਉਣ ਦੀ ਥਾਂ ਅੱਗੇ ਲੰਘ ਗਏ ਹੋਣਗੇ ਅਤੇ ਇਕ ਦੂਜੇ ਤੋਂ ਦੂਰ ਜਾ ਕੇ ਸਾਡੀ ਅਜੋਕੀ ਫੈਲਣ ਵਾਲੀ ਸ੍ਰਿਸ਼ਟੀ ਪੈਦਾ ਕਰ ਦਿੱਤੀ ਹੋਵੇਗੀ। ਹੁਣ ਅਸੀਂ ਇਹ ਕਿਵੇਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਾਡੀ ਸ੍ਰਿਸ਼ਟੀ ਦਾ ਅਰੰਭ ਮਹਾਨ ਧਮਾਕੇ ਤੋਂ ਹੀ ਹੋਇਆ ਹੈ? ਲਿਟਸੇ ਅਤੇ ਖਲਮੀਕੋਵ ਨੇ ਕੇਵਲ ਇਹ ਕੀਤਾ ਕਿ ਉਨ੍ਹਾਂ ਨੇ ਸ੍ਰਿਸ਼ਟੀ ਦੀ ਸਿਰਜਣਾ ਬਾਰੇ ਫੁਰਨੇ ਘੋਖੇ, ਜੋ ਫਰਾਈਡਮੈਨ ਦੇ ਫੁਰਨਿਆਂ ਵਰਗੇ ਸਨ, ਅਤੇ ਅਸਲੀ ਧਰਤੀ ਦੇ ਮੰਡਲਾਂ ਦੀਆਂ ਵਿੰਗੀਆਂ ਟੇਢੀਆਂ ਗਤੀਆਂ ਦੀ ਪੜਤਾਲ ਵੀ ਕੀਤੀ ਸੀ। ਉਨ੍ਹਾਂ ਨੇ ਪ੍ਰਗਟ ਕੀਤਾ ਕਿ ਇਹ ਫੁਰਨੇ ਮਹਾਨ ਧਮਾਕੇ ਦੀ ਦੇਣ ਹੋ ਸਕਦੇ ਹਨ, ਭਾਵੇਂ ਮੰਡਲ ਸਦਾ ਸਿੱਧੀਆਂ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚ ਇਕ ਦੂਜੇ ਤੋਂ ਦੂਰ ਨਹੀਂ ਜਾ ਰਹੇ। ਉਨ੍ਹਾਂ ਨੇ ਇਹ ਦਾਅਵਾ ਵੀ ਕੀਤਾ ਸੀ ਕਿ ਕੁਝ ਫੁਰਨਿਆਂ ਅਨੁਸਾਰ ਮੰਡਲਾਂ ਦਾ ਇਕ ਦੂਜੇ ਤੋਂ ਦੂਰ ਜਾਣਾ ਸੰਭਵ ਹੈ। ਉਨ੍ਹਾਂ ਨੇ ਦਲੀਲ ਦਿੱਤੀ ਸੀ ਕਿਉਂਕਿ ਫਰਾਈਡਮੈਨ ਦੇ ਫੁਰਨੇ ਵਰਗੇ ਹੋਰ ਵੀ ਬੇਸ਼ੁਮਾਰ ਫੁਰਨੇ ਪ੍ਰਤੀਤ ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਮਹਾਨ ਧਮਾਕੇ ਦੀ ਵਿਲੱਖਣਤਾ ਨਹੀਂ ਹੈ। ਇਸ ਲਈ ਅਸੀਂ ਇਸ ਨਤੀਜੇ ‘ਤੇ ਪਹੁੰਚ ਸਕਦੇ ਹਾਂ ਕਿ ਅਸਲ ਵਿੱਚ ਮਹਾਨ ਧਮਾਕਾ ਹੋਇਆ ਹੀ ਨਹੀਂ। ਮਗਰੋਂ ਜਾ ਕੇ ਉਹ ਸਮਝ ਗਏ ਸਨ, ਕਿ ਫਰਾਈਡਮੈਨ ਵਰਗੇ ਹੋਰ ਵੀ ਕਈ ਫੁਰਨੇ ਮੌਜੂਦ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਵਿਲੱਖਣਤਾ ਮੌਜੂਦ ਹੈ ਅਤੇ ਜਿਨ੍ਹਾਂ ਅਨੁਸਾਰ, ਮੰਡਲਾਂ ਨੂੰ ਕਿਸੇ ਖ਼ਾਸ ਦਿਸ਼ਾ ਵਿੱਚ ਚੱਲਣਾ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ। ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੇ 1970 ਵਿੱਚ ਆਪਣੀ ਦਲੀਲ ਵਾਪਸ ਲੈ ਲਈ ਸੀ।

ਲਿਟਸ਼ੇ ਅਤੇ ਖਲਮੀਕੋਵ ਦਾ ਕਾਰਜ ਇਸ ਲਈ ਕੀਮਤੀ ਵੀ ਸੀ ਕਿਉਂਕਿ ਇਸ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਸੀ ਕਿ ਧਰਤੀ ਵਿੱਚ ਵੀ ਵਿਲੱਖਣਤਾ ਹੋ ਸਕਦੀ ਹੈ, ਅਰਥਾਤ ਮਹਾਨ ਧਮਾਕੇ ਵਾਲੀ, ਜੇਕਰ ਅਨੁਪਾਤ ਦਾ ਆਮ ਸਿਧਾਂਤ ਸਹੀ ਮੰਨ ਲਿਆ ਜਾਵੇ । ਪਰੰਤੂ ਇਸ ਨਾਲ, ਅਸਲੀ ਪ੍ਰਸ਼ਨ ਦਾ ਹੱਲ ਨਹੀਂ ਸੀ ਨਿਕਲਿਆ । ਕੀ ਅਨੁਪਾਤ ਦਾ ਆਮ ਸਿਧਾਂਤ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਕਿ ਸਾਡੀ ਧਰਤੀ ਉੱਤੇ ਮਹਾਨ ਧਮਾਕਾ ਹੋਇਆ ਸੀ ? ਅਰਥਾਤ ਜਦੋਂ ਸਮੇਂ ਦਾ ਆਰੰਭ ਹੋਇਆ ਹੈ। ਇਸ ਪ੍ਰਸ਼ਨ ਦਾ ਉੱਤਰ 1965 ਵਿੱਚ ਬਰਤਾਨਵੀ ਗਣਿਤ ਅਤੇ ਫਿਜ਼ਿਕਸ ਵਿਗਿਆਨੀ ਰੋਜ਼ਰ ਪੈਨਰੋਜ਼ (Roger Penruse) ਦੇ ਉੱਕਾ ਹੀ ਵੱਖਰੇ ਵਿਚਾਰ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਇਆ ਹੈ। ਆਮ ਅਨੁਪਾਤ ਅਨੁਸਾਰ, ਰੌਸ਼ਨੀ ਦੀਆਂ ਕੋਣਾਂ ਦੇ ਅਮਲ ਦੀ ਅਤੇ ਇਸ ਅਮਲ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਕਿ ਖਿੱਚ ਸਦਾ ਹਾਵੀ ਹੋਇਆ ਕਰਦੀ ਹੈ, ਉਸ ਨੇ ਸਿੱਧ ਕਰ ਵਖਾਇਆ ਸੀ ਕਿ ਜਦੋਂ ਕੋਈ ਤਾਰਾ ਆਪਣੀ ਹੀ ਖਿੱਚ ਦੇ ਅਧੀਨ ਟੁੱਟ ਜਾਂਦਾ ਹੈ, ਉਹ ਅਜਿਹੀ ਥਾਂ ਘਿਰ ਜਾਂਦਾ ਹੈ, ਜਿਸ ਦੀ ਸਤਾਹ ਸੁੰਗੜ ਕੇ ਸਿਫਰ ਦੇ ਬਰਾਬਰ ਹੋ ਜਾਂਦੀ ਹੈ। ਇਸੇ ਤਰ੍ਹਾਂ ਉਸ ਦਾ ਆਕਾਰ ਵੀ ਸਿਫ਼ਰ ਦੇ ਬਰਾਬਰ ਹੋ ਜਾਂਦਾ ਹੈ। ਉਸ ਤਾਰੇ ਦਾ ਸਮੁੱਚਾ ਆਕਾਰ ਸਿਫ਼ਰ ਤੋਂ ਵੱਧ ਨਹੀਂ ਰਹਿੰਦਾ। ਇਸ ਲਈ ਪਦਾਰਥ ਦਾ ਸੰਘਣਾਪਣ ਅਤੇ ਪੁਲਾੜੀ ਸਮੇਂ ਦੀ ਰੇਖਾ ਦੀ ਸੀਮਾ ਹੀ ਨਹੀਂ ਰਹਿੰਦੀ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਇਕ ਵਿਲੱਖਣਤਾ ਪੁਲਾੜ-ਸਮੇਂ ਦੇ ਖਿੱਤੇ ਵਿੱਚ ਪੈਦਾ ਹੋ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਨੂੰ ਕਾਲੀ-ਮੋਰੀ (ਕਾਲਾ ਖੂਹ) ਕਹਿੰਦੇ ਹਨ।

ਪਹਿਲੀ ਨਜ਼ਰੇ, ਪੈਨਰੋਜ਼ ਦਾ ਸਿੱਟਾ, ਤਾਰਿਆਂ ਨਾਲ ਹੀ ਸੰਬੰਧਿਤ ਸੀ ਇਸ ਤੋਂ ਇਹ ਪਤਾ ਨਹੀਂ ਸੀ ਲੱਗਦਾ ਕਿ ਬ੍ਰਹਿਮੰਡ ਉੱਤੇ ਬੀਤੇ ਸਮੇਂ ਵਿੱਚ ਕਦੇ ਕੋਈ ਮਹਾਨ ਧਮਾਕਾ ਹੋਇਆ ਸੀ ਜਾਂ ਨਹੀਂ। ਪਰੰਤੂ, ਜਿਸ ਵੇਲੇ ਪੈਨਰੋਜ਼ ਨੇ ਆਪਣਾ ਸਿਧਾਂਤ ਪੇਸ਼ ਕੀਤਾ ਸੀ, ਉਸ ਵੇਲੇ ਮੈਂ ਖੋਜੀ ਵਿਦਿਆਰਥੀ ਵਜੋਂ ਆਪਣੇ ਪੀ.ਐਚ.ਡੀ. ਲਈ ਥੀਸਿਸ ਲਈ ਵਿਸ਼ੇ ਦੀ ਭਾਲ ਵਿੱਚ ਮਗਨ ਸਾਂ। ਇਸ ਤੋਂ ਦੋ ਸਾਲ ਪਹਿਲਾਂ ਮੇਰੀ ਤਸ਼ਖੀਸ ਹੋ ਗਈ ਸੀ ਕਿ ਮੈਂ (Als) ਦਾ ਰੋਗੀ ਹਾਂ। ਜਿਸ ਨੂੰ Lou Genrig ਦਾ ਰੋਗ ਜਾਂ ਮੋਟਰ ਨਿਉਰਾਨ (Neuron) ਰੋਗ ਕਹਿੰਦੇ ਹਨ। ਮੈਨੂੰ ਦੱਸਿਆ ਗਿਆ ਸੀ ਕਿ ਮੈਂ ਇਕ ਜਾਂ ਦੋ ਸਾਲ ਹੀ ਹੋਰ ਜੀਵਤ ਰਹਿ ਸਕਾਂਗਾ। ਅਜਿਹੀ ਹਾਲਤ ਵਿੱਚ, ਪੀ.ਐੱਚ.ਡੀ. ਲਈ ਪੜ੍ਹਨ ਦਾ ਕੋਈ ਅਰਥ ਹੀ ਨਹੀਂ ਸੀ। ਮੈਨੂੰ ਇਤਨਾ ਸਮਾਂ ਜੀਵਤ ਰਹਿਣ ਦੀ ਉਮੀਦ ਨਹੀਂ ਸੀ ਰਹੀ। ਪਰੰਤੂ ਦੋ ਸਾਲ ਬੀਤ ਗਏ ਅਤੇ ਮੇਰੀ ਸਿਹਤ ਪਹਿਲਾਂ ਨਾਲੋਂ ਮਾੜੀ ਨਹੀਂ ਸੀ ਹੋਈ। ਅਸਲ ਵਿੱਚ, ਹਾਲਤ ਪਹਿਲਾਂ ਨਾਲੋਂ ਚੰਗੇਰੀ ਹੋ ਗਈ ਸੀ ਅਤੇ ਇਕ ਅਤਿ ਨੇਕ ਲੜਕੀ ਨਾਲ ਮੇਰੀ ਮੰਗਣੀ ਵੀ ਹੋ ਗਈ ਸੀ, ਜਿਸ ਦਾ ਨਾਮ ਜੇਨ ਵਾਈਲਡ (Jane Wilde) ਸੀ। ਪਰੰਤੂ ਸ਼ਾਦੀ ਕਰਾਉਣ ਲਈ, ਮੈਨੂੰ ਕੋਈ ਨੌਕਰੀ ਮਿਲਣੀ ਚਾਹੀਦੀ ਸੀ ਅਤੇ ਨੌਕਰੀ ਲੱਭਣ ਲਈ, ਮੈਨੂੰ ਪੀ.ਐੱਚ.ਡੀ. ਕਰਨੀ ਜ਼ਰੂਰੀ ਸੀ।

1965 ਈਸਵੀ ਵਿੱਚ ਮੈਂ ਪੈਨਰੋਜ਼ ਦਾ ਸਿਧਾਂਤ ਪੜ੍ਹਿਆ ਕਿ ਜਿਹੜਾ ਬੰਦਾ ਖਿੱਚ ਦੇ ਆਧਾਰ ਸਦਕਾ ਢਹਿ-ਢੇਰੀ ਹੋ ਰਿਹਾ ਹੋਵੇ, ਉਹ ਬੰਦਾ ਇਕ ਵਿਲੱਖਣਤਾ ਬਣ ਸਕਦਾ ਹੈ। ਮੈਨੂੰ ਝਟਪਟ ਇਹ ਗੱਲ ਸਮਝ ਪੈ ਗਈ ਕਿ ਜੇ ਕੋਈ ਪੈਨਰੋਜ਼ ਦੇ ਸਿਧਾਂਤ ਵਿਚਾਲੇ ਸਮੇਂ ਦੀ ਦਿਸ਼ਾ ਉਲਟੀ ਕਰ ਦੇਵੇ ਤਾਂ ਜੋ ਗਿਰਾਵਟ ਦੀ ਥਾਂ ਫਲਾਵਟ ਲੈ ਲਵੇ, ਤਾਂ ਵੀ ਉਸ ਦਾ ਸਿਧਾਂਤ ਕਾਇਮ ਰਹਿ ਸਕਦਾ ਹੈ, ਪਰ ਸ਼ਰਤ ਇਹ ਹੈ ਕਿ ਬ੍ਰਹਿਮੰਡ ਇਸ ਵੇਲੇ ਵੱਡੀ ਪੱਧਰ ‘ਤੇ ਹੋਵੇ। ਫਰਾਈਡਮੈਨ ਦੇ ਫੁਰਨੇ ਅਨੁਸਾਰ ਪੈਨਰੋਜ਼ ਨੇ ਪ੍ਰਗਟ ਕਰ ਦਿੱਤਾ ਸੀ, ਟੁੱਟਣ ਵਾਲੇ ਤਾਰੇ ਦਾ ਅੰਤ ਇਕ ਵਿਲੱਖਣਤਾ ਵਿੱਚ ਹੋਵੇਗਾ। ਸਮੇਂ ਦੀ ਦਿਸ਼ਾ ਉਲਟਾਉਣ ਦੀ ਦਲੀਲ ਫਰਾਈਡਮੈਨ ਦੇ ਫੁਰਨੇ ਵਾਲੀ ਫੈਲਣ ਵਾਲੀ ਸ੍ਰਿਸ਼ਟੀ ਇਕ ਵਿਲੱਖਣਤਾ ਵਿੱਚੋਂ ਪੈਦਾ ਹੋਵੇਗੀ। ਤਕਨੀਕ ਦੇ ਪੱਖੋਂ, ਪੈਨਰੋਜ਼ ਦੇ ਸਿਧਾਂਤ ਨੂੰ ਇਸ ਗੱਲ ਦੀ ਲੋੜ ਸੀ ਕਿ ਬ੍ਰਹਿਮੰਡ ਦਾ ਪੁਲਾੜ-ਸੀਮਾ ਰਹਿਤ ਹੋਵੇ। ਇਸ ਲਈ ਮੈਂ ਇਸ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਇਹ ਸਿੱਧ ਕਰ ਸਕਦਾ ਸੀ ਕਿ ਵਿਲੱਖਣਤਾ ਦੀ ਲੋੜ ਕੇਵਲ ਉਸ ਵੇਲੇ ਪਵੇਗੀ ਜਦੋਂ ਬ੍ਰਹਿਮੰਡ ਇਤਨੀ ਤੇਜ਼ੀ ਨਾਲ ਫੈਲ ਰਿਹਾ ਹੋਵੇ, ਕਿ ਉਹ ਮੁੜ ਢਹਿ-ਢੇਰੀ ਨਾ ਹੋ ਜਾਵੇ (ਕਿਉਂਕਿ ਫਰਾਈਡਮੈਨ ਦੇ ਉਹ ਫੁਰਨੇ ਪੁਲਾੜ ਵਿੱਚ, ਸੀਮਾ-ਰਹਿਤ ਹਨ।)

ਅਗਲੇ ਕੁਝ ਹੀ ਸਾਲਾਂ ਵਿੱਚ, ਮੈਂ ਉਨ੍ਹਾਂ ਸਿਧਾਂਤਾਂ ਦੀਆਂ ਇਹ ਅਤੇ ਹੋਰ ਤਕਨੀਕੀ ਜ਼ਰੂਰਤਾਂ ਦੂਰ ਕਰਨ ਲਈ ਹੋਰ ਗਣਿਤ ਤਕਨੀਕਾਂ ਵਿਕਸਿਤ ਕਰ ਲਈਆਂ। ਜਿਹੜੀਆਂ ਸਾਬਤ ਕਰਦੀਆਂ ਸਨ ਕਿ ਵਿਲੱਖਣਤਾਵਾਂ ਵਾਪਰਨੀਆਂ ਜ਼ਰੂਰੀ ਹਨ। ਅੰਤ ਨਤੀਜੇ ਵਜੋਂ 1970 ਈਸਵੀ ਵਿੱਚ ਪੈਨਰੋਜ਼ ਅਤੇ ਮੇਰਾ ਇਕ ਸਾਂਝਾ ਪੱਤਰ ਪ੍ਰਕਾਸ਼ਤ ਹੋ ਗਿਆ। ਜਿਸ ਤੋਂ ਆਖ਼ਰ ਇਹ ਸਿੱਧ ਹੋ ਗਿਆ ਕਿ ਮਹਾਨ ਧਮਾਕੇ ਵਰਗੀ ਵਿਲੱਖਣਤਾ ਅਵੱਧ

ਵਾਪਰੀ ਹੋਵੇਗੀ, ਪਰ ਸ਼ਰਤ ਇਹ ਹੈ ਕਿ ਆਮ ਅਨੁਪਾਤ ਦਰੁੱਸਤ ਹੈ ਅਤੇ ਇਹ ਕਿ ਧਰਤੀ ਵਿੱਚ ਉਹ ਸਮੱਗਰੀ ਮੌਜੂਦ ਹੈ, ਜੋ ਸਾਨੂੰ ਨਜ਼ਰ ਆ ਰਹੀ ਹੈ। ਸਾਡੀ ਇਸ ਪ੍ਰਾਪਤੀ ਦੀ ਗੰਭੀਰ ਨੁਕਤਾਚੀਨੀ ਵੀ ਹੋਈ। ਕੁਝ ਵਿਰੋਧਤਾ ਰੂਸੀਆਂ ਵੱਲੋਂ ਹੋਈ ਕਿਉਂਕਿ ਉਹ ਵਿਗਿਆਨਿਕ ਨਿਰਣੇ ਪ੍ਰਤੀ ਮਾਰਕਸੀ ਵਿਸ਼ਵਾਸ ਦੇ ਧਾਰਨੀ ਸਨ ਅਤੇ ਕੁਝ ਕੁ ਵਿਰੋਧਤਾ ਉਨ੍ਹਾਂ, ਲੋਕਾਂ ਵੱਲੋਂ ਹੋਈ ਜਿਹੜੇ ਮਹਿਸੂਸ ਕਰਦੇ ਸਨ ਕਿ ਵਿਲੱਖਣਤਾਵਾਂ ਦਾ ਸਮੁੱਚਾ ਵਿਚਾਰ ਮੇਲ ਨਹੀਂ ਖਾਂਦਾ ਅਤੇ ਉਸ ਨਾਲ ਆਈਨਸਟਾਈਨ ਦੇ ਸਿਧਾਂਤ ਦੀ ਸੁੰਦਰਤਾ ਭੰਗ ਹੁੰਦੀ ਹੈ। ਪਰੰਤੂ ਕੋਈ ਵੀ ਗਣਿਤ ਸਿਧਾਂਤ ਦੇ ਵਿਰੁੱਧ ਦਲੀਲ ਪੇਸ਼ ਨਹੀਂ ਕਰ ਸਕਦਾ (ਅਜਿਹਾ ਕਰਨ ਦੀ ਗੁੰਜਾਇਸ਼ ਹੀ ਨਹੀਂ ਹੁੰਦੀ।) ਇਸ ਲਈ ਅੰਤ ਵਿੱਚ, ਸਾਡੀ ਪ੍ਰਾਪਤੀ ਆਮ ਤੌਰ ‘ਤੇ ਪ੍ਰਵਾਨ ਚੜ੍ਹ ਗਈ ਅਤੇ ਅੱਜ ਕੱਲ੍ਹ, ਹਰ ਕੋਈ ਇਹ ਸਵੀਕਾਰ ਕਰਨ ਲੱਗ ਪਿਆ ਹੈ ਕਿ ਬ੍ਰਹਿਮੰਡ ਦਾ ਮੁੱਢ ਮਹਾਨ ਧਮਾਕੇ ਦੀ ਵਿਲੱਖਣਤਾ ਤੋਂ ਹੀ ਹੋਇਆ ਹੈ। ਇਹ ਸ਼ਾਇਦ ਹੈਰਾਨੀਜਨਕ ਗੱਲ ਜਾਪੇਗੀ ਕਿ, ਮੇਰੇ ਵਿਚਾਰਾਂ ਵਿੱਚ ਪਲਟਾ ਆ ਗਿਆ ਹੈ ਕਿਉਂਕਿ ਮੈਂ ਹੁਣ ਦੂਜੇ ਵਿਜ਼ਿਕਸ ਵਿਗਿਆਨੀਆਂ ਨੂੰ ਵਿਸ਼ਵਾਸ ਦਿਵਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰ ਰਿਹਾ ਹਾਂ ਕਿ ਧਰਤੀ ਦੇ ਮੁਢ ਵੇਲੇ ਕੋਟੀ ਵਿਲੱਖਣ ਘਟਨਾ ਵਾਪਰੀ ਹੀ ਨਹੀਂ ਸੀ-ਕਿਉਂਕਿ ਅੱਗੇ ਜਾ ਕੇ ਅਸੀਂ ਦੇਖ ਲਵਾਂਗੇ ਕਿ ਮਿਕਦਾਰ ਦੇ ਅਸਰ ਪੈਣ ਸਾਰ, ਇਹ ਅਲੋਪ ਹੋ ਜਾਵੇਗੀ।

ਇਸ ਕਾਂਡ ਵਿੱਚ ਅਸੀਂ ਦੇਖ ਚੁੱਕੇ ਹਾਂ ਕਿ ਅੱਧੀ ਸ਼ਤਾਬਦੀ ਤੋਂ ਵੀ ਘੱਟ ਸਮੇਂ ਵਿੱਚ, ਬ੍ਰਹਿਮੰਡ ਸੰਬੰਧੀ ਮਨੁੱਖ ਦੇ ਵਿਚਾਰਾਂ ਵਿੱਚ ਜੋ ਕਈ ਜੁਗਾਂ ਵਿੱਚ ਬਣੇ ਸਨ, ਕਿਵੇਂ ਬਦਲ ਗਏ ਹਨ? ਹੁਬੱਲ (Hubble) ਦੀ ਇਹ ਖੋਜ ਕਿ ਧਰਤੀ ਫੈਲ ਰਹੀ ਹੈ ਅਤੇ ਧਰਤੀ ਦੇ ਆਪਣੇ ਗ੍ਰਹਿ ਦੇ ਨਿਗੂਣਾਪਣ, ਦੀ ਸਮਝ ਇਸ ਅਦਲਾ-ਬਦਲੀ ਦਾ ਆਰੰਭ ਸੀ। ਜਿਵੇਂ-ਜਿਵੇਂ ਤਜਰਬਾਤੀ ਅਤੇ ਵਿਚਾਰ-ਧਾਰਕ ਗਵਾਹੀ ਵੱਧਦੀ ਗਈ, ਤਿਵੇਂ-ਤਿਵੇਂ ਇਹ ਗੱਲ ਹੋਰ ਸਪੱਸ਼ਟ ਹੁੰਦੀ ਗਈ ਕਿ ਸਮੇਂ ਨੂੰ ਮੁਖ ਰੱਖ ਕੇ ਸ੍ਰਿਸ਼ਟੀ ਦਾ ਕਦੇ ਨਾ ਕਦੇ ਮੁੱਢ ਜ਼ਰੂਰ ਬੱਝਿਆ ਹੋਵੇਗਾ ਅਤੇ 1970 ਈ: ਵਿੱਚ ਪੈਨਰੋਜ਼ ਨੇ ਅਤੇ ਮੈਂ ਇਹ ਸਾਬਤ ਕਰ ਦਿੱਤਾ ਸੀ ਜਿਸ ਦਾ ਆਧਾਰ ਆਈਨਸਟਾਈਨ ਦਾ ਆਮ ਅਨੁਪਾਤ ਵਾਲਾ ਸਿਧਾਂਤ ਸੀ। ਇਹ ਸਾਬਤ ਹੋ ਗਿਆ ਸੀ ਕਿ ਅਨੁਪਾਤ ਦਾ ਆਮ ਸਿਧਾਂਤ ਇਕ ਅਧੂਰਾ ਸਿਧਾਂਤ ਹੈ। ਇਸ ਤੋਂ ਇਹ ਪਤਾ ਨਹੀਂ ਲੱਗਦਾ ਕਿ ਧਰਤੀ ਦਾ ਮੁੱਢ ਕਿਵੇਂ ਬੱਝਿਆ ਸੀ ਕਿਉਂਕਿ ਇਹ ਤਾਂ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਕਿ ਸਾਰੇ ਹੀ ਫਿਜ਼ੀਕਲ ਸਿਧਾਂਤ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ, ਇਹ ਸਿਧਾਂਤ ਵੀ ਸ਼ਾਮਿਲ ਹੈ, ਧਰਤੀ ਦੇ ਅਰੰਭ ਹੋਣ ਸਮੇਂ ਖੁਰਦ-ਬੁਰਦ ਹੋ ਜਾਂਦੇ ਹਨ। ਪਰੰਤੂ, ਆਮ ਅਨੁਪਾਤ ਸਿਧਾਂਤ ਤਾਂ ਇਕ ਅੰਸ਼ਕ ਸਿਧਾਂਤ ਹੀ ਹੈ। ਇਸ ਲਈ ਵਿਲੱਖਣਤਾ ਨਾਲ ਸੰਬੰਧਤ ਸਿਧਾਂਤ ਤਾਂ ਇਹੋ ਪ੍ਰਗਟ ਕਰਦੇ ਹਨ ਕਿ ਧਰਤੀ ਦਾ ਮੁੱਢ ਬੱਝਣ ਸਮੇਂ ਪਹਿਲਾਂ- ਪਹਿਲਾਂ, ਜਦੋਂ ਧਰਤੀ ਬਹੁਤ ਨਿੱਕੀ ਜਿਹੀ ਸੀ, ਸਮਾਂ ਜ਼ਰੂਰ ਮੌਜੂਦ ਹੋਇਆ ਹੋਵੇਗਾ, ਇਸ ਲਈ ਵੀਹਵੀਂ ਸ਼ਤਾਬਦੀ ਵਾਲੀ ਦੂਜੀ ਮਹਾਨ ਅੰਸ਼ਕ ਵਿਚਾਰ ਦੇ ਪੈਣ ਵਾਲੇ ਗੰਭੀਰ ਪ੍ਰਭਾਵਾਂ ਨੂੰ ਨਜ਼ਰ-ਅੰਦਾਜ਼ ਨਹੀਂ ਕਰ ਸਕਦਾ, ਅਰਥਾਤ ਮਿਕਦਾਰ ਗਿਣਤੀ ਮਿਣਤੀ ਨੂੰ। ਤਦ, 1970 ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ, ਅਸੀਂ ਇਕ ਬਹੁਤ ਵਿਸ਼ਾਲ ਧਰਤੀ ਦੀ ਥਾਂ ਇਕ ਨਿੱਕੀ ਜਿਹੀ ਧਰਤੀ ਦੀ ਖੋਜ ਵੱਲ ਆਪਣਾ ਧਿਆਨ ਕੇਂਦਰਿਤ ਕਰਨ ਲਈ ਮਜਬੂਰ ਹੋ ਗਏ ਸੀ। ਮਿਕਦਾਰ ਗਿਣਤੀ-ਮਿਣਤੀ ਦੇ ਇਸ ਸਿਧਾਂਤ ਬਾਰੇ, ਅੱਗੇ ਚੱਲ ਕੇ, ਦੇ ਅੰਸ਼ਕ ਸਿਧਾਂਤਾਂ ਨੂੰ ਇਕੱਲੀ ਖਿੱਚ ਵਾਲੀ ਥਿਊਰੀ ਬਣਾਉਣ ਦੀਆਂ ਕੋਸ਼ਿਸ਼ਾਂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਵਿਚਾਰ ਕਰਾਂਗੇ।

ਬੇ-ਭਰੋਸਗੀ ਦਾ ਅਸੂਲ

ਵਿਗਿਆਨਿਕ ਸਿਧਾਂਤਾਂ ਦੀ ਸਫ਼ਲਤਾ ਖ਼ਾਸ ਕਰਕੇ ਨਿਊਟਨ ਦੇ ਖਿੱਚ ਵਾਲੇ ਸਿਧਾਂਤ ਦੀ ਸਫ਼ਲਤਾ ਨੇ ਫ਼ਰਾਂਸ ਦੇ ਵਿਗਿਆਨਿਕ ਮਾਰਕੂਈ ਡੀ. ਲੈਪਲੇਸ ਨੂੰ ਉਨ੍ਹੀਵੀਂ ਸ਼ਤਾਬਦੀ ਦੇ ਅਰੰਭ ਵਿੱਚ ਹੀ ਇਹ ਦਲੀਲ ਦੇਣ ਲਈ ਉਤਸਾਹਿਤ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਬ੍ਰਹਿਮੰਡ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਿਰਣਾਇਕ ਹੈ। ਲੈਪਲੇਸ ਨੇ ਸੁਝਾਓ ਦਿੱਤਾ ਕਿ ਕੁਝ ਅਜਿਹੇ ਵਿਗਿਆਨਿਕ ਨਿਯਮ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਸਦਕਾ ਅਸੀਂ ਇਹ ਦੱਸਣ ਯੋਗ ਹੋ ਸਕੀਏ ਕਿ ਬ੍ਰਹਿਮੰਡ ਉੱਤੇ ਕੀ ਕੁੱਝ ਵਾਪਰਨ ਵਾਲਾ ਹੈ, ਜੇ ਸਾਨੂੰ ਇਸ ਦੀ ਹਾਲਤ ਦਾ ਇਕੋ ਸਮੇਂ ਪੂਰਾ ਗਿਆਨ ਹੋਵੇਗਾ। ਉਦਾਹਰਣ ਵਜੋਂ, ਜੇ ਸਾਨੂੰ ਸੂਰਜ ਦੀ ਸਥਿਤੀ, ਦੂਜੇ ਗ੍ਰਹਿਆਂ ਦੀ ਸਥਿਤੀ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਰਫ਼ਤਾਰਾਂ ਦਾ ਇਕੋ ਸਮੇਂ ਪੂਰਾ ਪਤਾ ਹੋਵੇ, ਤਾਂ ਅਸੀਂ ਨਿਊਟਨ ਦੇ ਨਿਯਮਾਂ ਦੀ ਵਰਤੋਂ ਨਾਲ ਸੂਰਜ ਮੰਡਲ ਦੀ ਹਾਲਤ ਕਿਸੇ ਹੋਰ ਸਮੇਂ ਸਮਝ ਸਕਾਂਗੇ। ਨਿਰਣਾ ਤਾਂ ਇਸ ਸੂਰਤ ਵਿੱਚ ਪ੍ਰਤੱਖ ਹੀ ਹੈ, ਪਰ ਲੈਪਲੇਸ ਤਾਂ ਇਹ ਵੀ ਸਮਝਦਾ ਹੈ ਕਿ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਨਿਯਮਾਂ ਨਾਲ ਦੂਜੀਆਂ ਚੀਜ਼ਾਂ ਵੀ ਸਮਝੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਮਨੁੱਖੀ ਚਿੰਤਨ ਵੀ ਸ਼ਾਮਿਲ ਹੈ।

ਵਿਗਿਆਨਿਕ ਨਿਰਣੇ ਦੇ ਅਸੂਲ ਦੀ ਬਹੁਤੇ ਲੋਕਾਂ ਨੇ ਵਿਰੋਧਤਾ ਕੀਤੀ ਸੀ। ਜਿਹੜੇ ਮਹਿਸੂਸ ਕਰਦੇ ਸਨ, ਕਿ ਇਸ ਨਾਲ ਸੰਸਾਰਕ ਕੰਮਾਂ ਵਿੱਚ ਈਸ਼ਵਰ ਨੂੰ ਦਖ਼ਲ ਦੇਣ ਦੀ ਖੁੱਲ੍ਹ ਵਿੱਚ ਵਿਘਨ ਪੈਂਦਾ ਹੈ। ਪਰੰਤੂ ਇਹ ਅਸੂਲ ਵਿਗਿਆਨਿਕ ਤੌਰ ‘ਤੇ ਵਰਤਮਾਨ ਸ਼ਤਾਬਦੀ ਦੇ ਮੁੱਢਲੇ ਸਾਲਾਂ ਤੱਕ ਕਾਇਮ ਰਿਹਾ। ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਇਹ ਸੰਕੇਤ ਕਿ ਇਹ ਵਿਸ਼ਵਾਸ ਛੱਡਣਾ ਹੀ ਪੈਣਾ ਹੈ, ਉਸ ਵੇਲੇ ਮਿਲਿਆ, ਜਦੋਂ ਬਰਤਾਨਵੀ ਵਿਗਿਆਨਿਕਾਂ ਲਾਰਡ ਰੈਲੇ (Rayleigh) ਅਤੇ ਸਰ ਜੇਮਜ਼ ਜੀਨਜ਼ ਦੇ ਹਿਸਾਬ- ਕਿਤਾਬ ਤੋਂ ਪ੍ਰਗਟ ਹੋ ਗਿਆ ਕਿ ਇਕ ਗਰਮ ਵਸਤੂ ਜਾਂ ਸਰੀਰ, ਜਿਵੇਂ ਇਕ ਤਾਰੇ ਵਿੱਚੋਂ ਅਸੀਮਤ ਰਫ਼ਤਾਰ ਨਾਲ ਸ਼ਕਤੀ ਨਿਕਲਣੀ ਚਾਹੀਦੀ ਹੈ। ਨਿਯਮਾਂ ਨੂੰ ਮੁਖ ਰੱਖ ਕੇ ਉਸ ਵੇਲੇ ਸਾਡਾ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਇਕ ਗਰਮ ਸ਼ਰੀਰ ਵਿੱਚੋਂ ਬਿਜਲਈ ਚੁੰਭਕ ਦੀਆਂ ਲਹਿਰਾਂ (ਜਿਵੇਂ ਕਿ ਰੇਡੀਉ ਲਹਿਰਾਂ, ਨਜ਼ਰ ਆਉਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਅਤੇ ਐਕਸ-ਰੇ ਲਹਿਰਾਂ) ਹਰ ਇਕ ਰਫ਼ਤਾਰ ਵਿੱਚ ਇਕੋ ਜਿੰਨੀਆਂ ਨਿਕਲਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ। ਉਦਾਹਰਣ ਵਜੋਂ, ਇਕ ਗਰਮ ਸਰੀਰ ਵਿੱਚੋਂ ਸ਼ਕਤੀਆਂ ਦੀਆਂ ਲਹਿਰਾਂ ਇਕੋ ਮਾਤਰਾ ਵਿੱਚ ਨਿਕਲਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ, ਜਦੋਂ ਕਿ ਰਫ਼ਤਾਰ ਦਸ ਲੱਖ ਤੋਂ ਵੀਹ ਲੱਖ ਲਹਿਰਾਂ ਪ੍ਰਤੀ ਸਕਿੰਟ ਹੋਵੇ। ਇਸ ਤਰ੍ਹਾਂ ਲਹਿਰਾਂ ਦੀ ਰਫ਼ਤਾਰ ਵੀਹ ਲੱਖ ਅਤੇ ਤੀਹ ਲੱਖ ਲਹਿਰਾਂ ਪ੍ਰਤੀ ਸਕਿੰਟ ਦੀ ਰਫ਼ਤਾਰ ਸਮੇਂ। ਹੁਣ ਕਿਉਂਕਿ ਲਹਿਰਾਂ ਦੀ ਗਿਣਤੀ ਪ੍ਰਤੀ ਸਕਿੰਟ ਦੀ ਕੋਈ ਸੀਮਾ ਨਹੀਂ ਹੈ, ਇਸ ਲਈ ਪੈਦਾ ਹੋਣ ਵਾਲੀ ਕੁਲ ਸ਼ਕਤੀ ਦੀ ਵੀ ਕੋਈ ਸੀਮਾ ਨਹੀਂ ਹੋ ਸਕਦੀ।

ਇਸ ਹਾਸੋਹੀਣੇ ਨਤੀਜੇ ਤੋਂ ਬਚਣ ਲਈ, ਜਰਮਨ ਵਿਗਿਆਨਿਕ ਮੈਕਸ ਪਲੈਂਕ (Max Planck) ਨੇ 1900 ਈ: ਵਿੱਚ ਸੁਝਾਉ ਦਿੱਤਾ, ਕਿ ਰੌਸ਼ਨੀ, ਐਕਸਰੇ ਅਤੇ ਦੂਜੀਆਂ ਲਹਿਰਾਂ ਇਕ ਮਨਮਰਜ਼ੀ ਦੀ ਰਫ਼ਤਾਰ ਨਾਲ ਪੈਦਾ ਨਹੀਂ ਹੋ ਸਕਦੀਆਂ, ਪਰੰਤੂ ਉਹ ਨਿਸ਼ਚਿਤ ਹਿਸਾਬ ਨਾਲ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਸ ਨੂੰ ਉਹ ਮਾਤਰਾ ਕਹਿੰਦਾ ਸੀ। ਫੇਰ ਹਰ ਇਕ ਮਾਤਰਾ ਵਿੱਚ ਖ਼ਾਸ ਸ਼ਕਤੀ ਹੁੰਦੀ ਹੈ ਜੋ ਲਹਿਰਾਂ ਬਣਨ ਦੀ ਮਾਤਰਾ ਬਹੁਤੀ ਰਫ਼ਤਾਰ ਵੇਲੇ ਬਹੁਤੀ ਹੋਇਆ ਕਰਦੀ ਹੈ, ਇਸ ਲਈ ਜ਼ਿਆਦਾ ਰਫ਼ਤਾਰ ਵੇਲੇ, ਇਕ ਮਾਤਰਾ ਪੈਦਾ ਕਰਨ ਲਈ, ਵਧੇਰੇ ਸ਼ਕਤੀ ਦੀ ਲੋੜ ਪਵੇਗੀ। ਇਸ ਤਰ੍ਹਾਂ, ਜ਼ਿਆਦਾ ਰਫ਼ਤਾਰ ਨਾਲ ਸ਼ਕਤੀ ਦੀ ਮਾਤਰਾ ਘੱਟ ਜਾਵੇਗੀ। ਇਸ ਲਈ ਜਿਸ ਰਫ਼ਤਾਰ ਨਾਲ ਕਿਸੇ ਵਜੂਦ ਵਿੱਚੋਂ ਸ਼ਕਤੀ ਪੈਦਾ ਹੋਵੇਗੀ। ਉਹ ਸੀਮਤ ਹੀ ਹੋਵੇਗੀ।

ਮਿਕਦਾਰ ਵਾਲੇ ਅੰਦਾਜ਼ੇ ਨਾਲ ਗਰਮ ਵਜੂਦਾਂ ਵਿੱਚੋਂ ਨਜ਼ਰ ਆਉਣ ਵਾਲੀ ਸ਼ਕਤੀ ਨਿਕਲਣ ਦੀ ਰਫ਼ਤਾਰ ਦੀ ਚੰਗੀ ਵਿਆਖਿਆ ਹੋ ਗਈ ਸੀ, ਪ੍ਰੰਤੂ ਇਸ ਦੀਆਂ ਨਿਰਣਾ ਕਰਨ ਵਾਲੀਆਂ ਗੁੰਝਲਾਂ ਦਾ 1926 ਤੱਕ ਪਤਾ ਨਹੀਂ ਸੀ ਲੱਗਿਆ। ਜਦੋਂ ਜਰਮਨੀ ਦੇ ਇਕ ਹੋਰ ਵਿਗਿਆਨੀ ਵਰਨਰ ਹੈਸਨਬਰਗ (Werner Hieisenberg) ਨੇ ਆਪਣਾ ਬੇਭਰੋਸਗੀ ਦੇ ਅਸੂਲ ਦਾ ਪ੍ਰਸਿੱਧ ਗੁਰ ਲੱਭ ਲਿਆ। ਕਿਸੇ ਵਸਤੂ ਦੀ ਭਵਿੱਖਤ ਸਥਿਤੀ ਅਤੇ ਰਫ਼ਤਾਰ ਦੱਸਣ ਲਈ, ਉਸ ਵਸਤੂ ਦੀ ਵਰਤਮਾਨ ਸਥਿਤੀ ਅਤੇ ਰਫ਼ਤਾਰ ਦੀ ਸਹੀ-ਸਹੀ ਮਿਣਤੀ ਕਰਨੀ ਜ਼ਰੂਰੀ ਹੈ। ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਉਸ ਵਸਤੂ ਉੱਤੇ ਸੁੱਟਣੀਆਂ ਪੈਂਦੀਆਂ ਹਨ। ਰੌਸ਼ਨੀ ਦੀਆਂ ਕੁਝ ਲਹਿਰਾਂ ਨੂੰ ਉਹ ਵਸਤੂ ਖਿਲਾਰ ਦਿੰਦੀ ਹੈ ਅਤੇ ਇਸ ਪ੍ਰਕਾਰ ਉਸ ਵਸਤੂ ਦੀ ਸਥਿਤੀ ਪ੍ਰਗਟ ਹੋ ਜਾਵੇਗੀ। ਪਰੰਤੂ ਉਸ ਵਸਤੂ ਦੀ ਅਧਿਕ ਸਹੀ ਸਥਿਤੀ ਨਿਸ਼ਚਿਤ ਕਰਨ ਲਈ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਦਾ ਆਪਸੀ ਫ਼ਾਸਲਾ ਵਧੇਰੇ ਸਹਾਇਕ ਸਿੱਧ ਹੁੰਦਾ ਹੈ। ਇਸ ਲਈ, ਇਕ ਵਸਤੂ ਦੀ ਸਹੀ-ਸਹੀ ਸਥਿਤੀ ਨਿਸ਼ਚਿਤ ਕਰਨ ਲਈ ਰੌਸ਼ਨੀ ਦੀਆਂ ਘੱਟ ਲੰਮੀਆਂ ਲਹਿਰਾਂ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦੀ ਲੋੜ ਪਵੇਗੀ। ਹੁਣ ਪਲੈਂਕ (Planck) ਦੇ ਮਿਕਦਾਰ ਵਾਲੇ ਗੁਰ ਅਨੁਸਾਰ ਕੋਈ ਘੱਟ ਤੋਂ ਘੱਟ ਰੌਸ਼ਨੀ ਆਪਣੀ ਮਰਜ਼ੀ ਨਾਲ ਵਰਤੋਂ ਨਹੀਂ ਕਰ ਸਕਦਾ, ਸਗੋਂ ਉਸ ਨੂੰ ਇਕ ਵਿਸ਼ੇਸ਼ ਮਿਕਦਾਰ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਹੀ ਪਵੇਗੀ। ਉਹ ਮਿਕਦਾਰ ਉਸ ਵਸਤੂ ਨੂੰ ਝੰਜੋੜ ਦੇਵੇਗੀ ਅਤੇ ਉਸ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਇਸ ਢੰਗ ਨਾਲ ਬਦਲ ਦੇਵੇਗੀ, ਜਿਸ ਦਾ ਨਿਰਣਾ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ। ਵਾਧੇ ਵਾਲੀ ਗੱਲ ਇਹ ਕਿ, ਵਸਤੂ ਦੀ ਜਿਤਨੀ ਵੱਧ ਸਹੀ ਗਿਣਤੀ ਕੀਤੀ ਜਾਵੇਗੀ, ਉਸੇ ਹਿਸਾਬ ਨਾਲ ਉਸ ਇਕੋ-ਇਕ ਮਿਕਦਾਰ ਦੀ ਵਧੇਰੇ • ਬਕਤੀ ਦੀ ਲੋੜ ਪਵੇਗੀ। ਇਸ ਲਈ ਉਸ ਵਸਤੂ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਵਡੇਰੀ ਮਾਤਰਾ (ਮਿਕਦਾਰ) ਖ਼ਰਾਬ ਕਰ ਸਕਦੀ ਹੈ। ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਵਸਤੂ ਦੀ ਸਥਿਤੀ ਮਿਣਨ ਲਈ ਤੁਸੀਂ ਵੱਧ ਤੋਂ ਵੱਧ ਕੋਸ਼ਿਸ਼ ਕਰੋਗੇ, ਉਸ ਦੀ ਰਫ਼ਤਾਰ ਦੀ ਮਿਣਤੀ ਉਤਨੀ ਹੀ ਘੱਟ ਨਹੀਂ ਕਰ ਸਕੋਗੇ। ਇਸ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਉਲਟਾਇਆ ਵੀ ਜਾ ਸਕਦਾ ਹੈ। ਹੈਸਨਬਰਗ (Heisenberg) ਨੇ ਸਿੱਧ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਵਸਤੂ ਦੀ ਸਥਿਤੀ ਅਤੇ ਉਸ ਦੀ ਰਫ਼ਤਾਰ ਬਾਰੇ ਬੇਡਰੋਸਗੀ ਅਨੁਸਾਰ, ਉਸ ਵਸਤੂ ਦਾ ਆਕਾਰ ਇਕ ਨਿਸ਼ਚਿਤ ਮਿਕਦਾਰ ਨਾਲੋਂ ਛੁਟੇਰਾ ਨਹੀਂ ਹੋ ਸਕਦਾ, ਜਿਸ ਨੂੰ ਪਲੈਂਕ (Planck) ਦੀ ਅਡੋਲ ਅਵਸਥਾ ਕਹਿੰਦੇ ਹਨ।

ਫੇਰ, ਇਹ ਹੱਦ ਉਸ ਢੰਗ ਉੱਤੇ ਨਿਰਭਰ ਨਹੀਂ ਹੈ, ਜਿਸ ਢੰਗ ਨਾਲ ਕੋਈ ਕਿਸੇ ਵਸਤੂ ਦੀ ਸਥਿਤੀ ਜਾਂ ਰਫ਼ਤਾਰ ਮਿਣਨ ਲਈ ਵਰਤਦਾ ਹੈ ਅਤੇ ਨਾ ਹੀ ਉਸ ਵਸਤੂ ਦੀ ਕਿਸਮ ਉੱਤੇ ਆਧਾਰਤ ਹੈ। ਹੈਸਨਬਰ  ਾ ਦਾ ਬੇਭਰੋਸਗੀ ਵਾਲਾ ਗੁਰ ਸੰਸਾਰ ਭਰ ਵਿੱਚ, ਮਿਣਤੀ ਦਾ ਸਭ ਤੋਂ ਪਕੇਰਾ ਅਤੇ ਪ੍ਰਮਾਣਤ ਗੁਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ।

ਬੇਭਰੋਸਗੀ ਦਾ ਗੁਰ ਦੁਨੀਆਂ ਬਾਰੇ ਵਿਚਤ ਬਣਾਉਣ ਦੇ ਢੰਗ ਵਿੱਚ ਗੁੰਝਲਾਂ ਵਾਲਾ ਹੈ। ਪੰਜਾਹ ਵਰ੍ਹੇ ਬੀਤਣ ਉਪਰੰਤ ਵੀ ਬਹੁਤ ਸਾਰੇ ਦਾਰਸ਼ਨਿਕਾਂ ਨੇ ਇਸ ਗੁਰ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਸਵੀਕਾਰ ਨਹੀਂ ਕੀਤਾ ਅਤੇ ਇਸ ਉੱਤੇ ਕਿੰਤੂ ਹੋ ਰਹੇ ਹਨ। ਬੇਭਰੋਸਗੀ ਦੇ ਗੁਰ ਨੇ ਲੈਪਲੇਸ (Laplace) ਦੇ ਉਸ ਵਿਗਿਆਨਿਕ ਸਿਧਾਂਤ ਦੇ ਸੁਪਨੇ ਨੂੰ ਖੇਰੂੰ-ਖੇਰੂੰ ਕਰਕੇ ਰੱਖ ਦਿੱਤਾ ਸੀ, ਅਰਥਾਤ ਅਜਿਹੀ ਦੁਨੀਆਂ, ਜਿਸ ਦਾ ਪੂਰਨ ਨਿਰਣਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਭਾਵੇਂ ਜਦੋਂ ਤੱਕ ਕੋਈ ਧਰਤੀ ਦੀ ਵਰਤਮਾਨ ਸਥਿਤੀ ਦਾ ਸਹੀ ਨਿਰਣਾ ਨਹੀਂ ਕਰ ਸਕਦਾ, ਉਦੋਂ ਤੱਕ ਭਵਿੱਖਾ ਘਟਨਾਵਾਂ ਬਾਰੇ ਭਵਿੱਖਬਾਣੀ ਵੀ ਨਹੀਂ ਕਰ ਸਕਦਾ। ਹਾਲੇ ਵੀ ਅਸੀਂ ਕਲਪਨਾ ਕਰ ਸਕਦੇ ਹਾਂ, ਕਿ ਕੁਝ ਅਜਿਹੇ ਨਿਯਮ ਮੌਜੂਦ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੁਆਰਾ ਘਟਨਾਵਾਂ ਨੂੰ ਨਿਸ਼ਚਿੰਤ ਕਰਨ ਲਈ ਕਰਾਮਾਤੀ ਸ਼ਕਤੀ ਬਣ ਸਕਦੇ ਹਨ। ਜਿਹੜੀ ਸ਼ਕਤੀ ਧਰਤੀ ਦੀ ਵਰਤਮਾਨ ਹਾਲਤ ਨੂੰ ਉਸ ਨੂੰ ਛੇੜੇ ਬਗ਼ੈਰ ਦੇਖ ਸਕਦੀ ਹੋਵੇ। ਪਰੰਤੂ ਸਾਡੇ ਵਰਗੇ ਫਾਤੀ ਲੋਕਾਂ ਨੂੰ ਸੰਸਾਰ ਦੇ ਅਜਿਹੇ ਨਮੂਨਿਆਂ ਵਿੱਚ ਕੋਈ ਰੁਚੀ ਨਹੀਂ। ਇਹ ਗੱਲ ਵਧੇਰੇ ਚੰਗੀ ਲੱਗਦੀ ਹੈ ਕਿ ਅਰਥਚਾਰੇ ਦੇ ਨਿਯਮ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਵੇ, ਜਿਸ ਨੂੰ ਉਕਮ (Occum) ਕਹਿੰਦੇ ਹਨ। ਉਸ ਨਾਲ ਸਿਧਾਂਤਾਂ ਦੇ ਉਹ ਸਾਰੇ ਪੱਖ ਕੱਟ ਦਿੱਤੇ ਜਾਣ, ਜੋ ਚੰਗੀ ਤਰ੍ਹਾਂ ਦੇਖੇ ਹੀ ਨਹੀਂ ਜਾ ਸਕਦੇ। ਇਸ ਵਿਚਾਰ ਨੇ ਸਨਬਰਗ, ਅਰਵਿਨ ਸਕਰੋਡਿੰਗਰ (Erwin Schrodinger) ਅਤੇ (Paul Dirac) ਪਾਲ ਡੀਰਾਕ ਨੂੰ 1920 ਵਿੱਚ ਪ੍ਰੇਰਿਆ ਕਿ ਮਿਕਦਾਰ ਦੇ ਗੁਰ ਨੂੰ ਨਵੇਂ ਸਿਰਿਓਂ ਮਿਕਦਾਰ ਮਸ਼ੀਨੀ ਗੁਰ ਵਿੱਚ ਬਦਲ ਦਿੱਤਾ ਜਾਵੇ। ਜਿਸ ਦਾ ਆਧਾਰ ਬੇਭਰੋਸਗੀ ਵਾਲਾ ਗੁਰ ਹੈ। ਇਸ ਸਿਧਾਂਤ ਅਨੁਸਾਰ ਵਸਤੂਆਂ ਦੀਆਂ ਵੱਖਰੀਆਂ, ਨਿਰਣਾਇਕ ਸਥਿਤੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਨਾ ਹੀ ਰਫ਼ਤਾਰਾਂ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਦੇਖਿਆ ਨਾ ਜਾ ਸਕੇ। ਸਗੋਂ ਉਨ੍ਹਾਂ ਦੀ ਮਿਕਦਾਰੀ ਹਾਲਤ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਵਿੱਚ ਸਥਿਤੀ ਅਤੇ ਰਫ਼ਤਾਰ ਸ਼ਾਮਿਲ ਹੁੰਦੀਆਂ ਹਨ। ਆਮ ਤੌਰ ‘ਤੇ, ਮਿਕਦਾਰ ਮਸ਼ੀਨਰੀ ਦੇਖਣ ਲਈ ਕੋਈ ਪੱਕਾ ਨਿਰਣਾ ਨਹੀਂ ਹੁੰਦਾ। ਇਸ ਦੇ ਉਲਟ, ਇਸ ਨਾਲ ਕਈ ਵੱਝਰੇ ਨਤੀਜੇ ਸਾਹਮਣੇ ਆਉਂਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਤੋਂ ਕੇਵਲ ਇਹ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਇਹ ਨਤੀਜੇ ਕਿਸ ਪ੍ਰਕਾਰ ਦੇ ਹਨ। ਕਹਿਣ ਦਾ ਭਾਵ ਹੈ ਕਿ ਜੇ ਕੋਈ ਇਕੋ ਪ੍ਰਕਾਰ ਦੇ ਢੰਗ ਵਰਤ ਕੇ ਵੱਡੇ ਪੈਮਾਨੇ ਉੱਤੇ ਇਕੋ ਪ੍ਰਕਾਰ ਦੇ ਨਤੀਜੇ ਕੱਢਦਾ ਹੈ, ਜਿਹੜੇ ਇਕੋ ਤਰੀਕੇ ਨਾਲ ਸ਼ੁਰੂ ਹੋਏ ਹੋਣ ਤਾਂ ਮਿਣਤੀ ਕਰਨ ਉੱਤੇ, ਇਕੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹਾਲਤਾਂ ਵਿੱਚ ੳ (A) ਨਿਕਲੇਗਾ; ਦੂਜੀਆਂ ਹਾਲਤਾਂ ਵਿੱਚ ਨਤੀਜਾ ਅ (B) ਨਿਕਲੇਗਾ ਅਤੇ ਇਹ ਸਿਲਸਿਲਾ ਇਸੇ ਪ੍ਰਕਾਰ ਚੱਲਦਾ ਰਹੇਗਾ। ਉ ਅਤੇ ਅ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ ਦੇ ਅੰਕਾਂ ਦਾ ਅੰਦਾਜ਼ਾ ਹੀ ਲੱਗ ਸਕੇਗਾ। ਪਰੰਤੂ ਕੋਈ ਵੀ ਇਕੱਲੀ-ਇਕੱਲੀ ਗਿਣਤੀ ਦੇ ਸਹੀ ਅੰਕਾਂ ਦਾ ਪਤਾ ਨਹੀਂ ਲਾ ਸਕੇਗਾ। ਇਸ ਲਈ ਮਿਕਦਾਰੀ ਮਸ਼ੀਨਰੀ ਦੁਆਰਾ ਵਿਗਿਆਨ ਵਿੱਚ ਅਨਿਸ਼ਚਿਤਤਾ ਜਾਂ ਅਟਕਲਪੱਚੂ ਤੱਤ ਪੈਦਾ ਹੋ ਜਾਂਦਾ ਹੈ। ਆਈਨਸਟਾਈਨ ਨੇ ਇਸ ਤੱਤ ਦੀ ਜ਼ੋਰਦਾਰ ਨੁਕਤਾਚੀਨੀ ਕੀਤੀ ਸੀ, ਹਾਲਾਂਕਿ ਉਸ ਨੇ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਚਾਰ ਵਿਕਸਿਤ ਕਰਨ ਲਈ ਅਤਿ ਮਹੱਤਵਪੂਰਨੇ ਭੂਮਿਕਾ ਨਿਭਾਈ ਸੀ। ਮਿਕਦਾਰੀ ਸਿਧਾਂਤ ਦੇ ਵਿਕਾਸ ਕਰਨ ਵਿੱਚ ਭੂਮਿਕਾ ਨਿਭਾਉਣ ਸਦਕਾ ਹੀ ਉਸ ਨੂੰ ਨੋਬਲ ਪੁਰਸਕਾਰ ਪ੍ਰਾਪਤ ਹੋਇਆ ਸੀ। ਫੇਰ ਵੀ, ਆਈਨਸਟਾਈਨ ਨੇ ਇਹ ਗੱਲ ਕਦੇ ਵੀ ਨਹੀਂ ਸੀ ਮੰਨੀ ਕਿ ਧਰਤੀ ਫਰਜ਼ੀ ਨਿਯਮਾਂ ਅਧੀਨ ਚੱਲ ਰਹੀ ਹੈ। ਉਸ ਦੇ ਵਿਚਾਰਾਂ ਦਾ ਖੁਲਾਸਾ, ਉਸ ਦੇ ਪ੍ਰਸਿੱਧ ਭਾਸ਼ਣ ਵਿੱਚ ਅੰਕਿਤ ਹੈ, “ਈਸ਼ਵਰ ਜੂਆ ਨਹੀਂ ਖੇਡਦਾ।” ਦੂਜੇ ਬਹੁਤ ਸਾਰੇ ਵਿਗਿਆਨਿਕ, ਮਿਕਦਾਰੀ ਮਸ਼ੀਨਰੀ ਨਾਲ ਇਸ ਲਈ ਸਹਿਮਤ ਹੋ ਗਏ ਸਨ, ਕਿਉਂਕਿ ਇਹ ਤਜਰਬਿਆਂ ਨਾਲ ਮੇਲ ਖਾਂਦੀ ਸੀ। ਸੱਚਮੁੱਚ ਇਹ ਸਿਧਾਂਤ ਅਧਿਕਤਰ ਸਫ਼ਲ ਹੋਇਆ ਹੈ ਅਤੇ ਇਹ ਆਧੁਨਿਕ ਵਿਗਿਆਨ ਕੈਮਿਸਟਰੀ ਅਤੇ ਤਕਨੀਕ ਦਾ ਆਧਾਰ ਵੀ ਹੈ। ਟਰਾਂਜ਼ਿਸਟਰ ਇਸ ਦੇ ਅਧੀਨ ਕੰਮ ਕਰਦੇ ਹਨ ਅਤੇ ਜੁੜਵੇਂ ਬਿਜਲਈ ਚੱਕਰ ਵੀ। ਜਿਹੜੇ ਬਿਜਲਈ ਸੰਦਾਂ (Quanta) ਦੇ ਜ਼ਰੂਰੀ ਅੰਗ ਹਨ। ਜਿਨ੍ਹਾਂ ਵਿੱਚ, ਟੈਲੀਵਿਜਨ ਅਤੇ ਕੰਪਿਊਟਰ ਸ਼ਾਮਿਲ ਹਨ ਅਤੇ ਇਹ ਆਧੁਨਿਕ ਕੈਮਿਸਟਰੀ ਤੇ ਜੀਵ ਵਿਗਿਆਨ ਦਾ ਆਧਾਰ ਹੈ। ਜਿਹੜੇ ਖੇਤਰਾਂ ਵਿੱਚ ਮਿਕਦਾਰੀ ਮਸ਼ੀਨਰੀ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਹੋਈ, ਉਹ ਫਿਜ਼ੀਕਲ ਵਿਗਿਆਨ ਦੇ ਖਿੱਚ ਦੇ ਸਿਧਾਂਤ ਅਤੇ ਧਰਤੀ ਦੀ ਵਿਸ਼ਾਲ ਬਣਤਰ ਹੈ।

ਭਾਵੇਂ ਰੌਸ਼ਨੀ, ਲਹਿਰਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਪਲੈਂਕ (Planck) ਦੇ ਮਿਕਦਾਰ ਸਿਧਾਂਤ ਅਨੁਸਾਰ ਐਉਂ ਪ੍ਰਤੀਤ ਹੁੰਦਾ ਹੈ ਕਿ ਇਹ ਨਿੱਕੇ-ਨਿੱਕੇ ਟੁਕੜਿਆਂ ਦੀ ਬਣੀ ਹੋਈ ਹੈ। ਇਸ ਨੂੰ ਡੱਬਿਆਂ ਵਿੱਚ ਪੈਦਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਜਾਂ ਸਾਂਭਿਆ ਜਾ ਸਕਦਾ ਹੈ ਜਾਂ ਮਿਕਦਾਰੀ ਬਕਸਿਆਂ ਵਿੱਚ।

ਐਨ ਇਸੇ ਤਰ੍ਹਾਂ, ‘ਹੈਜਨਬਰਗ ਦਾ ਅਨਿਸ਼ਚਿਤਤਾ ਦੇ ਸਿਧਾਂਤ ਦਾ ਅਰਥ ਹੈ ਕਿ ਟੁਕੜੇ ਕਦੇ-ਕਦੇ ਲਹਿਰਾਂ ਵਾਂਗ ਕੰਮ ਕਰਦੇ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਸਥਿਤੀ ਪੱਕੀ ਨਹੀਂ ਹੁੰਦੀ, ਸਗੋਂ ਲਿਬੜੇ-ਤਿਬੜੇ ਕੁਝ ਖਿਲਰੇ ਹੋਏ ਨਿਕਲਦੇ ਹਨ। ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਦਾ ਸਿਧਾਂਤ ਗਣਿਤ ਵਿਗਿਆਨ ਦੇ ਨਵੇਕਲੇ ਨਿਯਮ ਉੱਤੇ ਆਧਾਰਤ ਹੈ, ਜਿਹੜਾ ਧਰਤੀ ਦੀ ਵਿਆਖਿਆ ਟੁਕੜਿਆਂ ਅਤੇ ਲਹਿਰਾਂ ਨੂੰ ਮੁਖ ਰੱਖ ਕੇ ਨਹੀਂ ਕਰਦਾ। ਧਰਤੀ ਦੀ ਵਿਆਖਿਆ ਤਾਂ ਦ੍ਰਿਸ਼ਟੀ ਦੇ ਆਧਾਰ ‘ਤੇ ਹੀ ਕੀਤੀ ਜਾਂਦੀ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਵਿੱਚ ਲਹਿਰਾਂ ਅਤੇ ਟੁਕੜਿਆਂ ਵਿੱਚ ਦਵੰਦ ਹੈ। ਕੁਝ ਮਨੋਰਥਾਂ ਲਈ ਟੁਕੜਿਆਂ ਨੂੰ ਲਹਿਰਾਂ ਸਮਝ ਲੈਣਾ ਲਾਹੇਵੰਦ ਹੈ ਅਤੇ ਹੋਰਨਾਂ ਮਨੋਰਥਾਂ ਲਈ ਲਹਿਰਾਂ ਨੂੰ ਟੁਕੜੇ ਸਮਝਣਾ ਠੀਕ ਹੈ। ਇਸ ਦਾ ਇਕ ਅਤਿ ਮਹੱਤਵਪੂਰਨ ਸਿੱਟਾ ਇਹ ਹੈ ਕਿ ਲਹਿਰਾਂ ਜਾਂ ਟੁਕੜਿਆਂ ਦੇ ਸਮੂਹਾਂ ਵਿਚਲੀ ਡੂੰਘਾਈ (Troughs) ਜਾਂ ਟੁਕੜਿਆਂ ਦੇ ਸਮੂਹਾਂ ਵਿਚਲਾ ਦਖ਼ਲ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਐਉਂ ਕਹਿ ਲਵੋ ਕਿ ਲਹਿਰਾਂ ਦਾ ਇਕ ਜੋੜਾ ਦੂਜੇ ਜੋੜੇ ਦੀ ਡੂੰਘਾਈ ਨਾਲ ਮੇਲ ਖਾ ਸਕਦਾ ਹੈ। ਉਦੋਂ ਲਹਿਰਾਂ ਦੇ ਦੋ ਜੋੜੇ ਇਕ ਦੂਜੇ ਨੂੰ ਰੱਦ ਕਰ ਸਕਦੇ ਹਨ, ਨਾ ਕਿ ਮਿਲ ਕੇ ਇਕ ਵਧੇਰੇ ਬਲਵਾਨ ਲਹਿਰ ਪੈਦਾ ਕਰਨਗੇ, ਜਿਸ ਦੀ ਉਮੀਦ ਕੀਤੀ ਮਲੀ ਸੀ। ਦੇਖੋ (ਤਸਵੀਰ 4.1)। ਇਸੇ ਤਰ੍ਹਾਂ ਦੀ ਉਦਾਹਰਣ ਰੋਸ਼ਨੀ ਵਿੱਚ ਉਨ੍ਹਾਂ ਚੰਗੀ ਗਈ ਹੈ ਜਿਹੜੇ ਸਾਬਣ ਦੇ ਬੁਲਬੁਲਿਆਂ ਵਿੱਚ ਨਜ਼ਰ ਆਉਂਦੇ ਹੁੰਦੇ ਹਨ। ਇਹ ਰੰਗ ਪਾਣੀ ਦੇ ਬੁਲਬੁਲਿਆਂ ਦੀ ਫ਼ਿਲਮ ਦੇ ਦੋਹਾਂ ਪਾਸਿਆਂ ਤੋਂ ਪੈਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਨਾਲ ਪੈਦਾ ਹੁੰਦੇ ਹਨ। ਸਫ਼ੇਦ ਰੌਸ਼ਨੀ ਭਿੰਨ-ਭਿੰਨ ਲੰਬਾਈਆਂ ਅਤੇ ਰੰਗਾਂ ਵਾਲੀ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਨਾਲ ਬਣਦੀ ਹੈ । ਕੁਝ ਕੁ ਲੰਬਾਈਆਂ ਲਈ ਇਕ ਪਾਸਿਓਂ ਪੈਣ ਵਾਲੀ ਸਾਬਣ ਦੀ ਝਲਕ ਦੂਜੇ ਪਾਸਿਓਂ ਪੈਣ ਵਾਲੀ ਝਲਕ ਨਾਲ ਮੇਲ ਖਾ ਜਾਂਦੀ. ਹੈ। ਇਨ੍ਹਾਂ ਲਹਿਰਾਂ ਵਿਚਲੀ ਰੌਸ਼ਨੀ ਦੀ ਝਲਕ ਵਿੱਚੋਂ ਰੰਗ ਅਲੋਪ ਹੋ ਜਾਂਦੇ ਹਨ, ਜਿਹੜੀ ਉਸ ਵੇਲੇ ਰੰਗਦਾਰ ਪ੍ਰਤੀਤ ਹੋਇਆ ਕਰਦੀ ਹੈ।

ਟੁਕੜਿਆਂ (ਕਣਾਂ) ਦੇ ਰਸਤੇ ਵਿੱਚ ਵੀ ਔਕੜ ਆ ਸਕਦੀ ਹੈ, ਕਿਉਂਕਿ ਇਸ ਦਾ ਕਾਰਨ ਨਾਪ ਤੋਲ ਦਾ ਦੋਗਲਾਪਣ ਹੈ। ਪ੍ਰਸਿੱਧ ਉਦਾਹਰਣ ਦੋ ਚੀਰਿਆਂ ਵਾਲੇ ਤਜਰਬੇ

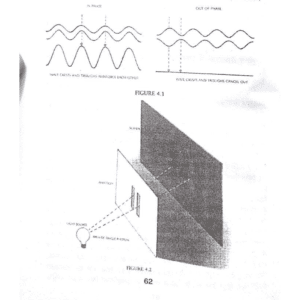
ਦੀ ਦਿੱਤੀ ਜਾ ਸਕਦੀ ਹੈ। (ਤਸਵੀਰ 4.2) ਇਸ ਵਿੱਚ ਦੋ ਤੰਗ ਮੁਸਾਵੀ ਲਕੀਰਾਂ ਸਦਕਾ ਹੋਈ ਵੰਡ ‘ਤੇ ਵਿਚਾਰ ਕਰ ਲਊ। ਵੰਡ ਦੇ ਇਕ ਪਾਸੇ ਕੋਈ ਇਕ ਖ਼ਾਸ ਰੰਗ ਦਾ ਲਾਟੂ ਜਗਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ (ਭਾਵ ਇਕ ਵਿਸ਼ੇਸ਼ ਲੰਬਾਈ ਦੀ ਲਹਿਰ ਤੋਂ ਹੈ।) ਬਹੁਤੀ ਰੌਸ਼ਨੀ ਵੰਡੀ ਹੋਈ ਥਾਂ ਉੱਤੇ ਪਵੇਗੀ ਅਤੇ ਥੋੜ੍ਹੀ ਜਿਹੀ ਰੌਸ਼ਨੀ ਪਾੜਾਂ ਵਿੱਚੋਂ ਲੰਘੇਗੀ। ਹੁਣ ਫ਼ਰਜ਼ ਕਰ ਲਉ ਕੋਈ ਰੋਸ਼ਨੀ ਤੋਂ ਉਲਟ ਪਾਸੇ ਦੂਰ ਜਾ ਕੇ ਇਕ ਪਰਚਾ ਟੰਗ ਦਿੰਦਾ ਹੈ। ਪਰਦੇ ਉਤਲੇ ਹਰ ਇਕ ਬਿੰਦੂ ਉੱਤੇ ਲਹਿਰਾਂ ਦੋਹਾਂ ਪਾੜਾਂ ਵਿੱਚੀਂ ਲੰਘ ਕੇ ਪੈਣਗੀਆਂ। ਪਰੰਤੂ ਆਮ ਤੌਰ ਤੇ, ਦੋਹਾਂ ਪਾੜਾਂ ਵਿੱਚੀਂ ਪਰਦੇ ਉੱਤੇ ਪੈਣ ਵਾਲੀ ਰੌਸ਼ਨੀ ਦਾ ਫ਼ਾਸਲਾ ਵੱਖਰਾ-ਵੱਖਰਾ ਹੋਵੇਗਾ। ਇਸ ਦਾ ਅਰਬ ਹੈ ਕਿ ਪਾੜਾਂ ਵਿੱਚੀਂ ਲੰਘਦੀਆਂ ਲਹਿਰਾਂ ਇਕ ਦੂਜੀ ਦੇ ਨੇੜੇ ਨਹੀਂ ਹੋਣਗੀਆਂ, ਜਦੋਂ ਉਹ ਪਰਦੇ ਉੱਤੇ ਪੈਣਗੀਆਂ। ਕੁਝ ਥਾਵਾਂ ’ਤੇ ਇਕ-ਦੂਜੀ ਨੂੰ ਕੱਟ ਦੇਣਗੀਆਂ ਅਤੇ ਦੂਜੀਆਂ ਥਾਂਵਾਂ ‘ਤੇ ਇਕ ਦੂਜੀ ਨੂੰ ਬਲ ਬਖ਼ਸ਼ਣਗੀਆਂ। ਨਤੀਜਾ ਰੌਸ਼ਨੀ ਅਤੇ ਹਨੇਰੇ ਦੇ ਆਪਣੇ-ਆਪਣੇ ਗੁਣਾਂ ਦਾ ਪ੍ਰਗਟਾਅ ਹੈ।

ਸਭ ਤੋਂ ਵਧੀਆ ਗੱਲ ਤਾਂ ਇਹ ਹੈ ਕਿ ਰੌਸ਼ਨੀ ਦੇ ਸੋਮੇ ਨੂੰ ਕਣਾਂ ਦੇ ਸੋਮੇ ਵਿੱਚ ਬਦਲ ਦੇਵੇ, ਭਾਵ ਇਕ ਬੰਨ੍ਹਵੀਂ ਰਫ਼ਤਾਰ ਵਾਲੇ ਇਲੈਕਟਰੋਨਾਂ ਨਾਲ, ਤਾਂ ਇਕੋ ਪ੍ਰਕਾਰ ਦੀਆਂ ਕਨਾਰੀਆਂ ਪ੍ਰਾਪਤ ਹੋਣਗੀਆਂ (ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਵਿਰੋਧੀ ਲਹਿਰਾਂ ਦੀ ਲੰਬਾਈ ਨਿਸ਼ਚਿਤ ਹੋਇਆ ਕਰਦੀ ਹੈ।) ਇਹ ਇਕ ਅਨੋਖੀ ਅਤੇ ਵਚਿਤਰ ਗੱਲ ਹੈ ਕਿਉਂਕਿ ਜੇ ਕਿਸੇ ਕੋਲ ਇਕੋ ਪਾੜ ਹੋਵੇ, ਤਾਂ ਕੋਈ ਕਨਾਰੀ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦੀ, ਸਗੋਂ ਪਰਦੇ ਉੱਤੇ ਇਲੈਕਟਰੋਨ ਇਕੋ ਜਿਹੇ ਢੰਗ ਨਾਲ ਖਿੰਡੇ ਹੋਏ ਦਿਸਣਗੇ। ਇਸ ਲਈ ਇਹ ਸੋਚ ਪੈਦਾ ਹੋਵੇਗੀ ਕਿ ਇਕ ਧਾੜ (ਚੀਰ) ਪਰਦੇ ਉਤਲੇ ਹਰ ਇਕ ਬਿੰਦੂ ਉੱਤੇ ਪੈਣ ਵਾਲੇ ਇਲਕਟਰੋਨਾਂ ਦੀ ਗਿਣਤੀ ਵੱਧ ਜਾਵੇਗੀ ਪਰੰਤੂ ਦਖ਼ਲ (ਖਲਲ) ਸਦਕਾ ਅਸਲ ਵਿੱਚ ਕਈ ਥਾਵਾਂ ਤੇ ਇਹ ਗਿਣਤੀ ਘੱਟ ਜਾਇਆ ਕਰਦੀ ਹੈ। ਜੇ ਇਲੈਕਟਰੋਨ ਚੀਰਾਂ ਵਿੱਚੀਂ ਇਕ-ਇਕ ਕਰਕੇ ਲੰਘਾਏ ਜਾਣ ਤਾਂ ਐਉਂ ਜਾਪੇਗਾ ਕਿ ਉਥੇ ਕੇਵਲ ਇਕ ਹੀ ਚੀਰ ਹੈ—ਜਿਸ ਕਰਕੇ ਪਰਦੇ ਉੱਤੇ ਉਨ੍ਹਾਂ ਦਾ ਖਿਲਾਰਾ ਇਕੋ ਜਿਹਾ ਹੈ। ਪਰੰਤੂ, ਅਸਲ ਵਿੱਚ, ਜਦੋਂ ਇਲੈਕਟਰੋਨ ਇਕ-ਇਕ ਕਰਕੇ ਲੰਘਾਏ ਜਾਂਦੇ ਹਨ, ਉਦੋਂ ਵੀ ਕਨਾਰੀਆਂ (ਝਾਲਰਾਂ) ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ। ਇਸ ਲਈ, ਹਰ ਇਕ ਇਲੈਕਟਰੋਨ ਦੋਹਾਂ ਚੀਰਾਂ ਵਿੱਚੋਂ ਇਕੋ ਸਮੇਂ ਲੰਘਣੇ ਚਾਹੀਦੇ ਹਨ। ਕਣਾਂ ਵਿੱਚ ਪੈਣ ਵਾਲੇ ਵਿਘਨ ਦੀ ਸਮੱਸਿਆ ਐਟਮਾਂ ਨੂੰ ਸਮਝਣ ਲਈ ਅਤਿ ਜ਼ਰੂਰੀ ਹੈ, ਕੈਮਿਸਟਰੀ, ਬਾਇਓਲੋਜੀ ਜਾਂ ਸਰੀਰਾਂ ਦੀ ਬਣਤਰ ਸਮਝਣ ਲਈ ਅਤਿ ਜ਼ਰੂਰੀ ਹੈ, ਜਿਨ੍ਹਾਂ ਦੁਆਰਾ ਅਸੀਂ ਅਤੇ ਸਾਡੇ ਦੁਆਲੇ ਦੀ ਹਰ ਇਕ ਵਸਤੂ, ਪੈਦਾ ਹੁੰਦੀ ਹੈ। ਸ਼ਤਾਬਦੀ ਦੇ ਅਰੰਭ ਵਿੱਚ, ਐਉਂ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ਕਿ ਐਟਮ (Atoms) ਵੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮਣ ਵਾਲੇ ਮੰਡਲਾਂ ਵਰਗੇ ਹੀ ਹਨ। ਉਨ੍ਹਾਂ ਦੇ ਨਾਲ ਇਲੇਕਟਰੋਨ (ਉਲਟੀ ਬਿਜਲੀ ਦੇ ਕਣ) ਜੋ (ਸਿੱਧੀ ਬਿਜਲੀ ਰੱਖਣ ਵਾਲੇ ਕਣ।) ਇਕ ਕੇਂਦਰੀ ਬਿੰਦੂ ਦੁਆਲੇ ਘੁੰਮ ਰਹੇ ਹਨ। ਸਿੱਧੀ ਅਤੇ ਪੁੱਠੀ ਬਿਜਲੀ ਵਿਚਲੀ ਖਿੱਚ ਬਾਰੇ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ਕਿ ਇਹ ਇਲੈਕਟਰੋਨਾਂ ਨੂੰ ਘੁਮਾਈ ਜਾਂਦੀ ਹੈ, ਜਿਵੇਂ ਸੂਰਜ ਅਤੇ ਗ੍ਰਹਿਆਂ ਵਿਚਲੀ ਖਿੱਚ ਸਦਕਾ ਗ੍ਰਹਿ ਘੁੰਮਦੇ ਰਹਿੰਦੇ ਹਨ। ਇਸ ਸੋਚ ਵਿੱਚ ਇਕ ਔਕੜ ਇਹ ਸੀ ਕਿ ਮਸ਼ੀਨੀ ਅਤੇ ਬਿਜਲਈ ਨਿਯਮ, ਜੋ ਮਿਕਦਾਰੀ ਹਿਸਾਬ-ਕਿਤਾਬ ਤੋਂ ਪਹਿਲਾਂ ਬਣੇ ਹੋਏ ਸਨ, ਪ੍ਰਗਟ ਕਰਦੇ ਸਨ ਕਿ ਇਲੈਕਟਰੋਨਾਂ ਦੀ ਸ਼ਕਤੀ ਖ਼ਤਮ ਹੋ ਜਾਵੇਗੀ ਅਤੇ ਉਹ ਉਦੋਂ ਤੱਕ ਅੰਦਰ ਨੂੰ ਜਾਂਦੇ ਰਹਿਣਗੇ, ਜਦੋਂ ਤੱਕ ਕੇਂਦਰ ਬਿੰਦੂ ਨਾਲ ਟਕਰਾ ਨਹੀਂ ਜਾਂਦੇ। ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਐਟਮ ਅਤੇ ਸੱਚਮੁੱਚ, ਸਮੁੱਚਾ ਪਦਾਰਥ, ਪੂਰੀ ਤਰ੍ਹਾਂ ਸੁੰਗੜ ਕੇ ਗਾਹੜੇ ਹੋ ਜਾਣਗੇ। ਇਸ ਸਮੱਸਿਆ ਦਾ ਅੰਸ਼ਕ ਹੱਲ 1913 ਵਿੱਚ, ਡੈਨਮਾਰਕ ਦੇ ਵਿਗਿਆਨੀ ਨੀਲਜ਼ ਬੈਹਰ (Niels Bohr) ਨੇ ਲੱਭਿਆ ਸੀ। ਉਸ ਦਾ ਸੁਝਾਉ ਸੀ ਕਿ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਇਲੈਕਟਰੋਨ ਕੇਂਦਰ ਬਿੰਦੂ ਤੋਂ ਹਰ ਇਕ ਫ਼ਾਸਲੇ ਤੇ ਖਹਿ ਕੇ ਘੁੰਮਣ ਦੇ ਯੋਗ ਨਾ ਹੋਣ, ਸਗੋਂ ਕੁਝ ਨਿਸ਼ਚਿਤ ਫ਼ਾਸਲਿਆਂ ਤੋਂ ਹੀ ਘੁੰਮ ਸਕਦੇ ਹੋਣ। ਜੇ ਕੋਈ ਇਹ ਵੀ ਫ਼ਰਜ਼ ਕਰ ਲਵੇ ਕਿ ਇਕ ਜਾਂ ਦੋ ਇਲੈਕਟਰੋਨ ਕਿਸੇ ਇਕ ਫ਼ਾਸਲੇ ‘ਤੇ ਘੁੰਮ ਸਕਦੇ ਹੋਣ ਤਾਂ ਐਟਮਾਂ ਦੇ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀ ਸਮੱਸਿਆ ਦਾ ਹੱਲ ਨਿਕਲ ਸਕਦਾ ਹੈ ਕਿਉਂਕਿ ਇਲੈਕਟਰੋਨ ਘੱਟ ਤੋਂ ਘੱਟ ਫ਼ਾਸਲਿਆਂ ਅਤੇ ਸ਼ਕਤੀਆਂ ਦੇ ਚੱਕਰਾਂ ਦੀ ਥਾਂ ਲੈਣ ਤੋਂ ਅੱਗੇ ਨਹੀਂ ਜਾ ਸਕਦੇ।

ਇਸ ਵਿਚਾਰ ਨਾਲ ਸਭ ਤੋਂ ਸਾਧਾਰਣ ਐਟਮ, ਹਾਈਡਰੋਜਨ ਦੀ ਬਣਤਰ ਦੀ ਵਿਆਖਿਆ ਹੋ ਗਈ ਸੀ, ਜਿਸ ਵਿੱਚ ਕੇਂਦਰ ਬਿੰਦੂ ਦੁਆਲੇ ਘੁੰਮਣ ਵਾਲਾ ਕੇਵਲ ਇਕੋ ਇਕ ਇਲੈਕਟਰੋਨ ਹੈ। ਪਰੰਤੂ ਇਸ ਨਾਲ ਇਹ ਸਪੱਸ਼ਟ ਨਹੀਂ ਸੀ ਹੋਇਆ ਕਿ ਇਸ ਦੀ ਵਰਤੋਂ ਬਹੁਤੇ ਪੇਚੀਦਾ ਐਟਮਾਂ ਪ੍ਰਤੀ ਕਿਵੇਂ ਵਧਾਈ ਜਾਵੇ। ਫੇਰ ਪ੍ਰਮਾਣਤ ਘੇਰਿਆਂ ਵਾਲਾ ਵਿਚਾਰ ਆਪਹੁਦਰਾ ਹੀ ਸੀ। ਮਿਕਦਾਰੀ ਹਿਸਾਬ-ਕਿਤਾਬ ਦੇ ਨਵੇਂ ਸਿਧਾਂਤ ਨੇ ਇਹ ਔਕੜ ਦੂਰ ਕਰ ਦਿੱਤੀ ਸੀ। ਇਸ ਨੇ ਸਪੱਸ਼ਟ ਕਰ ਦਿੱਤਾ ਕਿ ਧੁਰੇ ਦੁਆਲੇ ਘੁੰਮਣ ਵਾਲੇ ਇਲੈਕਟਰਾਨ ਨੂੰ ਇਕ ਅਜਿਹੀ ਲਹਿਰ ਮੰਨਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਸ ਦੀ ਲੰਬਾਈ ਉਸ ਦੀ ਰਫ਼ਤਾਰ ਉੱਤੇ ਨਿਰਭਰ ਹੋਵੇ। ਕੁਝ ਚੱਕਰਾਂ ਲਈ, ਚੱਕਰ (ਘੇਰੇ) ਦੀ ਲੰਬਾਈ ਇਲੈਕਟਰੋਨ ਦੀਆਂ ਲਹਿਰਾਂ ਦੀ ਲੰਬਾਈ ਦੇ ਪੂਰੇ ਅੰਕ ਦੇ ਬਰਾਬਰ ਹੋਵੇਗੀ। (ਨਾ ਕਿ ਉਸ ਅੰਕ ਦੇ ਅੰਸ਼ ਦੇ ਬਰਾਬਰ)। ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਚੱਕਰਾਂ ਵਿੱਚ ਹਰ ਗੇੜੇ ਵਿੱਚ, ਲਹਿਰ ਦੀ ਟੀਸੀ ਇਕੋ ਸਥਿਤੀ ਵਿੱਚ ਰਹੇਗੀ, ਅਤੇ ਇਸ ਲਈ ਲਹਿਰਾਂ ਇਕੱਠੀਆਂ ਹੁੰਦੀਆਂ ਰਹਿਣਗੀਆਂ। ਇਹ ਚੱਕਰ ਬੋਹਰ (BoHR) ਦੇ ਪ੍ਰਮਾਣਤ ਚੱਕਰਾਂ ਦੇ ਬਰਾਬਰ ਹੋਣਗੇ। ਪਰੰਤੂ ਜਿਹੜੇ ਚੱਕਰਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਲਹਿਰਾਂ ਦੀ ਲੰਬਾਈ ਦੇ ਇਕੱਲੇ ਅਤੇ ਪੂਰੇ ਅੰਕ ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਹੋਣਗੀਆਂ, ਹਰ ਇਕ ਲਹਿਰ ਦੀ ਸਿਖਰ ਉਸ ਦੀ ਡੂੰਘਾਈ ਰੱਦ ਕਰ ਦੇਵੇਗੀ, ਜਿਉਂ-ਜਿਉਂ ਇਲੈਕਟਰੋਨ ਚੱਕਰ ਕੱਟੀ ਜਾਣਗੇ, ਉਨ੍ਹਾਂ ਚੱਕਰਾਂ ਨੂੰ ਮਾਣਤਾ ਨਹੀਂ ਦਿੱਤੀ ਜਾਵੇਗੀ।

ਲਹਿਰ ਕਣ ਦੇ ਦੋਗਲੇਪਣ ਨੂੰ ਪਰਖਣ ਦਾ ਵਧੀਆ ਢੰਗ ਤਾਂ ਅਮਰੀਕਨ ਵਿਗਿਆਨੀ ਰਿਚਰਡ ਫੇਸਮੈਨ (Richard Feysman) ਵੱਲੋਂ ਪੇਸ਼ ਕੀਤਾ ਇਤਿਹਾਸਕ . ਸਮੂਹ ਹੈ। ਇਸ ਵਿਚਾਰ ਅਨੁਸਾਰ ਪੁਲਾੜ-ਸਮੇਂ ਵਿੱਚ ਅੰਕ ਦਾ ਨਿਵੇਕਲਾ ਇਤਿਹਾਸ ਜਾਂ ਰਸਤਾ ਨਹੀਂ ਹੋਇਆ ਕਰਦਾ, ਜਿਵੇਂ ਕਿ ਪੁਰਾਣੇ ਅਤੇ ਮਿਕਦਾਰ-ਰਹਿਤ ਸਿਧਾਂਤ ਅਧੀਨ ਹੋਇਆ ਕਰਦਾ ਹੈ। ਇਸ ਦੇ ਉਲਟ ਇਹ ਤਾਂ A ਤੋਂ B ਤੱਕ ਹਰ ਸੰਭਵ ਰਸਤੇ ਰਾਹੀਂ ਜਾ ਸਕਦਾ ਹੈ। ਹਰ ਇਕ ਰਸਤੇ ਨਾਲ, ਅੰਕਾਂ ਦੇ ਜੋੜੇ ਜੁੜੇ ਹੋਏ ਹੁੰਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇਕ ਲਹਿਰ ਦੇ ਆਕਾਰ ਨੂੰ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ ਅਤੇ ਦੂਜਾ ਘੇਰੇ ਵਿਚਲੀ ਉਸ ਦੀ ਸਥਿਤੀ ਨੂੰ (ਭਾਵ ਕੀ ਇਹ ਸਿਥਰ ਹੈ ਜਾਂ ਡੂੰਘਾਈ।) A ਤੋਂ B ਤੱਕ ਜਾਣ ਦਾ ਅੰਦਾਜ਼ਾ ਸਾਰੇ ਰਸਤਿਆਂ ਦੀਆਂ ਲਹਿਰਾਂ ਦਾ ਜੋੜ ਕਰਕੇ ਲਾਇਆ ਜਾਂਦਾ ਹੈ। ਆਮ ਤੌਰ ‘ਤੇ ਜੇ ਕੋਈ ਪੜੋਸੀ ਰਸਤਿਆਂ ਦਾ ਟਾਕਰਾ ਕਰ ਕੇ ਦੇਖੇ, ਤਾਂ ਘੇਰਿਆਂ ਵਿੱਚ, ਉਨ੍ਹਾਂ ਦੇ ਪੜਾਅ ਅਤੇ ਸਥਿਤੀਆਂ ਵੱਖਰੀਆਂ ਹੋਣਗੀਆਂ। ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਇਨ੍ਹਾਂ ਰਸਤਿਆਂ ਨਾਲ ਜੁੜੀਆਂ ਹੋਈਆਂ ਲਹਿਰਾਂ ਇਕ-ਦੂਜੀ ਨੂੰ ਕੱਟ ਦੇਣਗੀਆਂ। ਪਰੰਤੂ, ਕੁਝ-ਕੁਝ ਪੜੋਸੀ ਸਤਿਆਂ ਵਿੱਚ, ਸਥਿਤੀ ਵਿੱਚ ਕੋਈ ਫ਼ਰਕ ਨਹੀਂ ਹੋਵੇਗਾ। ਇਨ੍ਹਾਂ ਰਸਤਿਆਂ ਦੀਆਂ ਲਹਿਰਾਂ ਇਕ-ਦੂਜੀ ਨੂੰ ਨਹੀਂ ਕੱਟਣਗੀਆਂ। ਅਜਿਹੇ ਰਸਤੇ ਬੋਹਰ (Bohr) ਅਨੁਸਾਰ ਪ੍ਰਮਾਣਤ ਮੰਨੇ ਜਾਣਗੇ।

ਇਨ੍ਹਾਂ ਵਿਚਾਰਾਂ ਅਧੀਨ, ਪੱਕੇ ਹਿਸਾਬੀ ਰੂਪ ਵਿੱਚੋਂ, ਵਧੇਰੇ ਪੇਚੀਦਾ ਐਟਮਾਂ (Molecules) ਸਗੋਂ ਪ੍ਰਮਾਣੂਆਂ ਨੂੰ ਜਿਹੜੇ ਘੇਰਿਆਂ ਵਿਚਲੇ ਦੇ ਘੇਰਿਆਂ ਨੂੰ ਕੁਝ ਸੌਖੇ ਢੰਗ ਨਾਲ ਗਿਣਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਇਲੈਕਟਰੋਨਾਂ ਦੁਆਰਾ ਇਕੱਠੇ ਕੀਤੇ ਹੋਏ ਐਟਮਾਂ ਦੇ ਬਣੇ ਹੋਏ ਹੁੰਦੇ ਹਨ। ਜਿਹੜੇ ਘੇਰੇ ਇਕ ਨਾਲੋਂ ਵਧੀਕ ਧੁਰਿਆਂ ਦੁਆਲੇ ਕੱਢੇ ਜਾਂਦੇ ਹਨ। ਕਿਉਂਕਿ ਪਰਮਾਣੂਆਂ ਦੀ ਬਣਤਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਆਪਸੀ ਖਹਿਬਾਜ਼ੀ ਸਮੁੱਚੀ ਕੈਮਿਸਟਰੀ ਅਤੇ ਬਾਇਓਲੋਜੀ ਦਾ ਆਧਾਰ ਹਨ, ਇਸ ਲਈ ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਦੁਆਰਾ ਸਾਡੇ ਚਾਰੇ ਪਾਸੇ ਫੈਲੀਆਂ ਸਾਰੀਆਂ ਵਸਤਾਂ ਨੂੰ ਪ੍ਰਗਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਪਰ ਉਸ ਹਦ ਤੱਕ, ਜਿਹੜੀ ਹੱਦ ਅਨਿਸ਼ਚਿਤਤਾ ਦੇ ਅਸੂਲ ਅਧੀਨ ਆਉਂਦੀ ਹੈ। ਪਰੰਤੂ ਅਸਲੀਅਤ ਇਹ ਹੈ ਕਿ ਅਸੀਂ ਉਨ੍ਹਾਂ ਢੰਗਾਂ ਦਾ ਪਤਾ ਨਹੀਂ ਲਾ ਸਕਦੇ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ, ਕਈ ਬਹੁਤ ਹੀ ਪੇਚੀਦਾ ਇਲੈਕਟਰੋਨਾਂ ਦਾ ਹਿਸਾਬ ਲਾਉਣਾ ਪੈਂਦਾ ਹੋਵੇ।

ਐਉਂ ਜਾਪਦਾ ਹੈ ਕਿ ਆਈਨਸਟਾਈਨ ਦਾ ਅਨੁਪਾਤ ਦਾ ਸਿਧਾਂਤ ਧਰਤੀ ਦੀ ਵਿਸ਼ਾਲ ਬਣਤਰ ਪ੍ਰਗਟ ਕਰਦਾ ਹੈ। ਇਸ ਨੂੰ ਪ੍ਰਮਾਣਤ ਸਿਧਾਂਤ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਅਰਥਾਤ ਇਹ ਮਿਕਦਾਰ ਹਿਸਾਬ ਅਨਿਸ਼ਚਿਤਾ ਦੇ ਅਸੂਲ ਦੀ ਪ੍ਰਵਾਹ ਨਹੀਂ ਕਰਦਾ, ਤਾਂ ਜੋ ਦੂਜੇ ਸਿਧਾਂਤਾਂ ਨਾਲ ਮੇਲ ਖਾ ਸਕੇ। ਇਸ ਦਾ ਕਾਰਨ ਕਿ ਇਸ ਨਾਲ ਦੇਖਣ ਵੇਲੇ ਕੋਈ ਵਿਘਨ ਨਹੀਂ ਪੈਂਦਾ, ਇਹ ਹੈ ਕਿ ਸਾਡੇ ਤਜਰਬੇ ਅਨੁਸਾਰ ਚੁੰਭਕ ਖੇਤਰ ਬਹੁਤ ਕਮਜ਼ੋਰ ਹਨ। ਪਰੰਤੂ ਪਹਿਲਾਂ ਵਿਚਾਰੀ ਜਾ ਚੁੱਕੀ ਵਿਲੱਖਣਤਾ ਤੋਂ ਸੰਕੇਤ ਮਿਲਦਾ ਹੈ ਕਿ ਚੁੰਭਕ ਸ਼ਕਤੀ ਦੋ ਮੌਕਿਆਂ ਉੱਤੇ ਬਹੁਤ ਬਲਵਾਨ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ-ਕਾਲੇ ਖੂਹਾਂ ਵੇਲੇ (Black Holes) ਅਤੇ ਮਹਾਨ ਧਮਾਕੇ ਵੇਲੇ। ਅਜਿਹੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਖੇਤਰਾਂ ਵਿੱਚ, ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਦੇ ਪ੍ਰਭਾਵਾਂ ਦੀ ਬਹੁਤ ਮਹੱਤਤਾ ਹੈ। ਇਸ ਪ੍ਰਕਾਰ, ਪ੍ਰਾਚੀਨ ਸਾਧਾਰਣ ਅਨੁਪਾਤ, ਅਥਾਹ ਸੰਘਣੇਪਣ ਦੇ ਨੁਕਤੇ ਦੱਸਣ ਸਦਕਾ, ਆਪਣੇ ਵਿਕਾਸ ਦੀ ਘੋਸ਼ਣਾ ਵੀ ਕਰਦੀ ਹੈ। ਐਨ ਉਸ ਤਰ੍ਹਾਂ ਜਿਵੇਂ ਪ੍ਰਾਚੀਨ (ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਤੋਂ ਸੱਖਣੀ) ਹਿਸਾਬ ਨੇ ਇਹ ਦੱਸ ਕੇ ਕਿ ਐਟਮ ਸੰਘਣੇ ਹੋ ਕੇ ਨਸ਼ਟ ਹੋ ਜਾਣਗੇ, ਆਪਣੇ ਹੀ ਵਿਨਾਸ਼ ਦੀ ਘੋਸ਼ਣਾ ਕੀਤੀ ਸੀ। ਹਾਲੇ ਤੱਕ, ਸਾਡੇ ਕੋਲ ਕੋਈ ਵੀ ਅਜਿਹਾ ਸਿਧਾਂਤ ਨਹੀਂ ਹੈ, ਜੋ ਆਮ ਅਨੁਪਾਤ ਅਤੇ ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਨੂੰ ਜੋੜ ਦੇਵੇ, ਪਰੰਤੂ ਸਾਨੂੰ ਅਜਿਹੇ ਸਿਧਾਂਤਾਂ ਦੇ ਪੱਖਾਂ ਦਾ ਪਤਾ ਜ਼ਰੂਰ ਹੈ। ਕਾਲੇ ਥੂਹਾਂ ਅਤੇ ਮਹਾਨ ਧਮਾਕੇ ਉੱਤੇ ਪੈਣ ਵਾਲੇ ਪਰਤ ਦਾ ਜ਼ਿਕਰ ਅਗਲੇ ਕਾਂਡ ਵਿੱਚ ਕੀਤਾ ਜਾਵੇਗਾ। ਹਾਲ ਦੀ ਘੜੀ ਤਾਂ ਅਸੀਂ ਕੁਦਰਤ ਦੀਆਂ ਹੋਰ ਸ਼ਕਤੀਆਂ ਨੂੰ ਸਮਝਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਵਿੱਚ ਹਾਂ ਜਿਸ ਨਾਲ ਇਕੋ ਇਕ ਇਕਜੁਟ ਮਿਕਦਾਰੀ ਸਿਧਾਂਤ ਪ੍ਰਾਪਤ ਹੋ ਸਕੇ।

ਮੁੱਢਲੇ ਕਣ ਅਤੇ ਕੁਦਰਤੀ ਸ਼ਕਤੀਆਂ

ਅਰਸਤੂ ਦਾ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਧਰਤੀ ਚਾਰ ਤੱਤਾਂ, ਮਿੱਟੀ, ਵਾਯੂ, ਅਗਨੀ ਅਤੇ ਪਾਣੀ ਦੀ ਬਣੀ ਹੋਈ ਹੈ। ਇਨ੍ਹਾਂ ਤੱਤਾਂ ਨੂੰ ਦੋ ਸ਼ਕਤੀਆਂ, ਹਰਕਤ ਵਿੱਚ ਲਿਆਉਂਦੀਆਂ ਹਨ : ਧਰਤੀ ਖਿੱਚਣ ਲਈ, ਪਾਣੀ ਨਿਘਰਨ ਲਈ, ਹੋਛਾਪਣ ਜਾਂ ਚੰਚਲਤਾ ਚਲਦੇ ਰਹਿਣ ਲਈ ਅਤੇ ਅਗਨੀ ਉੱਪਰ ਨੂੰ ਚੜ੍ਹਨ ਲਈ। ਧਰਤੀ ਦੇ ਇਨ੍ਹਾਂ ਤੱਤਾਂ ਦਾ ਵੰਡਵਾਰਾ-ਪਦਾਰਥ ਅਤੇ ਸ਼ਕਤੀਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਅੱਜਕੱਲ੍ਹ ਵੀ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ। ਅਰਸਤੂ ਦਾ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਪਦਾਰਥ ਸਦਾ ਕਾਇਮ ਰਹਿਣ ਵਾਲਾ ਹੈ। ਭਾਵ ਪਦਾਰਥ ਨੂੰ ਅਣਗਿਣਤ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਇਹ ਕਦੇ ਵੀ ਦੇਖਣ ਵਿੱਚ ਨਹੀਂ ਆਇਆ ਕਿ ਪਦਾਰਥ ਦੇ ਕਿਸੇ ਵੀ ਕਣ ਦੇ ਹੋਰ ਟੁਕੜੇ ਨਾ ਕੀਤੇ ਜਾ ਸਕਣ। ਪਰੰਤੂ ਯੂਨਾਨ ਦੇ ਕੁਝ ਵਸਨੀਕਾਂ ਦਾ ਵਿਚਾਰ ਸੀ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਡੈਮੋਕਰਾਈਟਸ (Democrites) ਸ਼ਾਮਿਲ ਸੀ, ਕਿ ਪਦਾਰਥ ਸੁਭਾਵਿਕ ਤੌਰ ‘ਤੇ ਕਣਾਂ ਦਾ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਅਤੇ ਹਰ ਇਕ ਵਸਤੂ ਕਈ ਕਿਸਮ ਦੇ ਅਣਗਿਣਤ (Atoms) ਦੀ ਬਣੀ ਹੋਈ ਹੁੰਦੀ ਹੈ। ਯੂਨਾਨੀ ਭਾਸ਼ਾ ਵਿੱਚ, ਐਟਮ ਦਾ ਅਰਥ ਵੰਡੀ ਨਾ ਜਾਣ ਵਾਲੀ ਵਸਤੂ ਹੈ। ਸਦੀਆਂ ਵਾਲੀ ਇਹ ਦਲੀਲ ਪ੍ਰਚੱਲਤ ਰਹੀ ਅਤੇ ਦੋਹਾਂ ਵਿਚਾਰਾਂ ਵਿੱਚੋਂ ਕਿਸੇ ਦੇ ਪੱਖ ਵਿੱਚ ਕੋਈ ਸਬੂਤ ਨਾ ਮਿਲਿਆ, ਪਰੰਤੂ 1803 ਈ: ਵਿੱਚ, ਬਰਤਾਨਵੀ ਕੈਮਿਸਟਰੀ ਅਤੇ ਫਿਜ਼ਿਕਸ ਦੇ ਮਾਹਰ ਜੌਹਨ ਡਾਲਟਨ (John Dalton) ਨੇ ਪ੍ਰਸ਼ਨ ਉਠਾਇਆ ਕਿ ਸਦਾ ਕੀਮੀਆਈ ਮਿਸ਼ਰਣਾਂ ਨੂੰ ਕੁਝ ਅਨੁਪਾਤ ਵਿੱਚ ਮਿਲਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਐਟਮਾਂ ਨੂੰ ਵੰਡ ਕੇ ਨਿੱਕੀਆਂ ਇਕਾਈਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਸਮਝਾਇਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਪ੍ਰਮਾਣੂ ਜਾਂ ਕਣ ਕਹਿੰਦੇ ਹਨ। ਫੇਰ ਵੀ, ਦੋ ਵਿਚਾਰਾਂ ਵਿੱਚੋਂ ਐਟਮਾਂ ਦਾ ਪੱਖ ਪੂਰਨ ਵਾਲਿਆਂ ਦੇ ਹੱਕ ਵਿੱਚ ਚਾਲੂ ਸ਼ਤਾਬਦੀ ਦੇ ਅੰਤਮ ਸਾਲਾਂ ਤੱਕ ਅੰਤਮ ਫ਼ੈਸਲਾ ਨਹੀਂ ਸੀ ਹੋਇਆ। ਹਾਂ ਆਈਨਸਟਾਈਨ ਨੇ ਇਕ ਅਤਿ ਮਹੱਤਵਪੂਰਨ ਸਬੂਤ ਸਾਖਸ਼ਾਤ ਰੂਪ ਵਿੱਚ ਜ਼ਰੂਰ ਪੇਸ਼ ਕਰ ਦਿੱਤਾ ਸੀ। 1905 ਈ: ਵਿੱਚ ਲਿਖੇ ਇਕ ਪਰਚੇ ਵਿੱਚ, ਵਿਸ਼ੇਸ਼ ਅਨੁਪਾਤ ਸੰਬੰਧੀ ਲਿਖੇ ਪਰਚੇ ਤੋਂ ਕੁਝ ਹੀ ਹਫ਼ਤੇ ਪਹਿਲਾਂ, ਆਈਨਸਟਾਈਨ ਨੇ ਦੱਸਿਆ ਸੀ ਕਿ ਜਿਸ ਹਰਕਤ ਨੂੰ (Brownion) ਬਰਾਊਨੀ ਹਰਕਤ ਕਹਿੰਦੇ ਹਨ- ਅਰਥਾਤ ਤਰਲ ਪਦਾਰਥ ਵਿੱਚ ਲਟਕ ਰਹੇ ਧੂੜ ਦੇ ਨਿੱਕੇ ਕਣਾਂ ਦੀ ਬੇ-ਹਿਸਾਬੀ ਅਤੇ ਆਪ-ਹੁਦਰੀ ਹਰਕਤ ਦੀ ਵਿਆਖਿਆ ਤਰਲ ਪਦਾਰਥ ਵਿਚਲੇ ਐਟਮਾਂ ਦੀ ਰੇਤ ਦੇ ਕਣਾਂ ਨਾਲ ਖਹਿਬਾਜ਼ੀ ਵਜੋਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।

ਉਸ ਵੇਲੇ ਤੱਕ ਇਹ ਸ਼ੱਕ ਮੌਜੂਦ ਰਿਹਾ ਸੀ ਕਿ ਇਹ ਐਟਮ ਵੰਡੇ ਨਹੀਂ ਜਾ ਸਕਦੇ। ਕਈ ਸਾਲ ਪਹਿਲਾਂ, ਟ੍ਰਿਨਿਟੀ ਕਾਲਜ ਕੈਂਬ੍ਰਿਜ (Trinity College Cambridge) ਦੇ ਵਿਦਵਾਨ ਜੇ.ਜੇ. ਥਾਮਸ (J.J. Thomas) ਨੇ ਤਜਰਬੇ ਦੁਆਰਾ ਇਹ ਸਿੱਧ ਕਰ ਦਿੱਤਾ ਸੀ ਕਿ ਪਦਾਰਥ ਦਾ ਇਕ ਅਜਿਹਾ ਕਣ ਮੌਜੂਦ ਹੈ, ਜਿਸ ਨੂੰ ਕਣ ਜਾਂ ਇਲਕੈਟਰੋਨ ਬਹਿੰਦੇ ਹਨ, ਜਿਸ ਦਾ ਆਕਾਰ ਹੌਲੇ ਤੋਂ ਹੌਲੇ ਐਟਮ ਦੇ ਇਕ ਹਜ਼ਾਰਵੇਂ ਹਿੱਸੇ ਤੋਂ ਵੀ ਘੱਟ ਹੁੰਦਾ ਹੈ। ਉਸ ਨੇ ਅਜੋਕੇ T.V. ਦੀ ਤਸਵੀਰ ਵਾਲੀ ਨਾਲੀ ਵਰਗੀ ਚੀਜ਼ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਸੀ। ਇਕ ਸਖ਼ਤ ਧਾਤ ਦੀ ਰਿਸ਼ਮ ਵਿੱਚੋਂ ਇਲੈਕਟਰੋਨ ਪੈਦਾ ਹੋ ਗਏ, ਕਿਉਂਕਿ ਇਨ੍ਹਾਂ ਵਿੱਚ ਉਲਟੀ ਤਸਵੀਰ ਹੋਇਆ ਕਰਦੀ ਹੈ, ਇਸ ਲਈ ਬਿਜਲਈ ਖੇਤਰ ਨੂੰ ਵਰਤ ਕੇ, ਕਾਂਸੀ ਦੇ ਮੁਲਮੇ ਵਾਲੇ ਪਰਦੇ ਵੱਲ ਧੱਕਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਜਦੋਂ ਉਹ ਪਰਦੇ ਨਾਲ ਟਕਰਾਉਂਦੇ ਸਨ, ਰੌਸ਼ਨੀ ਦੀ ਲਿਸ਼ਕੋਰ ਪੈਦਾ ਹੋ ਜਾਂਦੀ ਸੀ। ਛੇਤੀ ਹੀ ਇਹ ਗੱਲ ਸਮਝ ਵਿੱਚ ਆ ਗਈ ਸੀ ਕਿ ਇਹ ਇਲੈਕਟਰੋਨ ਐਟਮਾਂ ਵਿੱਚੋਂ ਹੀ ਨਿਕਲਦੇ ਹੋਣਗੇ ਅਤੇ 1911 ਈ: ਵਿੱਚ ਬਰਤਾਨਵੀਂ ਫਿਜ਼ਿਕਸ ਦੇ ਮਾਹਰ ਅਰਨੈਸਟ ਰੁਥਰਫੋਰਡ (Earnest Rutherford) ਨੇ ਜ਼ਾਹਰ ਕਰ ਵਿਖਾਇਆ ਕਿ ਪਦਾਰਥਕ ਐਟਮਾਂ ਦੀ ਆਪਣੀ ਅੰਦਰੂਨੀ ਬਣਤਰ ਹੁੰਦੀ ਹੈ। ਭਾਵ ਉਹ ਅਤਿ ਨਿੱਕੇ-ਨਿੱਕੇ ਬਿਜਲੀ ਦੇ ਸਿੱਧੇ ਢੰਗ ਨਾਲ ਭਰੇ ਹੋਏ ਧੁਰਿਆਂ ਦੇ ਬਣੇ ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੁਆਲੇ ਕੁਝ ਇਲੈਕਟਰੋਨ ਗੇੜੇ ਕੱਢਦੇ ਰਹਿੰਦੇ ਹਨ। ਉਸ ਨੇ ਇਹ ਗੱਲ ਉਸ ਢੰਗ ਦਾ ਵਿਸ਼ਲੇਸ਼ਨ ਕਰਕੇ ਸਿੱਧ ਕੀਤੀ ਸੀ ਜਿਸ ਅਨੁਸਾਰ ਐਟਮ ਦੇ ਕਣ, ਜਿਹੜੇ ਰੇਡੀਆਈ ਐਟਮਾਂ ਵਿੱਚੋਂ ਨਿਕਲਦੇ ਹਨ ਅਤੇ ਸਿੱਧੀ ਬਿਜਲੀ ਨਾਲ ਭਰਪੂਰ ਹੁੰਦੇ ਹਨ, ਉਹ ਐਟਮਾਂ ਨਾਲ ਟਕਰਾਉਣ ਨਾਲ ਥਿੜਕ ਜਾਂਦੇ ਹਨ।

ਪਹਿਲਾਂ-ਪਹਿਲਾਂ ਤਾਂ ਇਹ ਸੋਚਿਆ ਜਾਂਦਾ ਸੀ ਕਿ ਐਟਮ ਦਾ ਧੁਰਾ ਇਲੈਕਟਰੋਨਾਂ ਅਤੇ ਸਿੱਧੀ ਬਿਜਲੀ ਵਾਲੇ ਕਣਾਂ ਦਾ ਬਣਿਆ ਹੁੰਦਾ ਹੈ। ਜਿਸ ਕਣ ਨੂੰ ਪ੍ਰੋਟੋਨ (Proton) ਕਹਿੰਦੇ ਹਨ, ਜਿਸ ਦਾ ਅਰਥ ਯੂਨਾਨੀ ਭਾਸ਼ਾ ਵਿੱਚ ਪ੍ਰਥਮ ਹੈ, ਕਿਉਂਕਿ ਉਦੋਂ ਇਹ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ਕਿ ਇਹ ਪਦਾਰਥ ਦੇ ਕਣਾਂ ਦੀ ਮੁੱਢਲੀ ਇਕਾਈ ਹੈ। ਪਰੰਤੂ 1932 ਈ: ਵਿੱਚ ਕੈਂਬਰਿਜ ਦੇ ਰੁਥਰਫੋਰਡ ਦੇ ਸਾਥੀ ਜੇਮਜ਼ ਚੈਡਵਿਕ (ਜਾਮੇਸ Chadwick) ਨੇ ਇਹ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕਰ ਲਈ ਕਿ ਧੁਰੇ ਵਿੱਚ ਇਕ ਹੋਰ ਕਣ ਵੀ ਮੌਜੂਦ ਹੈ, ਇਸ ਨੂੰ ਨਿਊਟਰੋਨ (Neutron) ਕਹਿੰਦੇ ਹਨ, ਜਿਸ ਦਾ ਆਕਾਰ ਪ੍ਰੋਟੋਨ ਦੇ ਬਰਾਬਰ ਹੀ ਹੋਇਆ ਕਰਦਾ ਹੈ, ਪਰੰਤੂ ਉਸ ਵਿੱਚ ਬਿਜਲੀ ਨਹੀਂ ਹੁੰਦੀ। ਚੈਡਵਿਕ ਨੂੰ ਇਸ ਪ੍ਰਾਪਤੀ ਲਈ ਨੋਬਲ ਪੁਰਸਕਾਰ ਮਿਲਿਆ ਸੀ ਅਤੇ ਉਸ ਨੂੰ (Cowville) ਅਤੇ (Cairys) ਕਾਲਜ ਕੈਂਬਰਿਜ ਦਾ ਮਾਸਟਰ ਚੁਣ ਲਿਆ ਗਿਆ ਸੀ। ਜਿਹੜੇ ਕਾਲਜ ਦਾ ਮੈਂ ਅੱਜ ਕਲ੍ਹ ਫੈਲੇ ਹਾਂ।) ਪਿੱਛੋਂ ਜਾ ਕੇ ਉਸ ਨੇ ਮਾਸਟਰ ਵਜੋਂ ਅਸਤੀਫ਼ਾ ਦੇ ਦਿੱਤਾ ਸੀ ਕਿਉਂਕਿ ਦੂਜੇ ਸਾਥੀਆਂ ਨਾਲ ਉਸ ਦੇ ਵਿਚਾਰ ਨਹੀਂ ਸਨ ਮਿਲਦੇ। ਉਸ ਕਾਲਜ ਵਿੱਚ, ਉਸ ਤੋਂ ਮਗਰੋਂ ਜਦੋਂ ਨੌਜਵਾਨ ਸਾਥੀ ਲੜਾਈ ਤੋਂ ਪਰਤ ਆਏ ਸਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੇ ਪੁਰਾਣੇ ਸਾਥੀਆਂ ਦੇ ਵਿਰੁੱਧ ਮਤਦਾਨ ਕਰ ਦਿੱਤਾ ਸੀ, ਜਿੱਥੇ ਉਹ ਲੰਮੇ ਸਮੇਂ ਤੋਂ ਬਿਰਾਜਮਾਨ ਰਹੇ ਸਨ। ਅਜਿਹਾ ਮੇਰੇ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਹੋ ਚੁੱਕਿਆ ਸੀ। ਮੈਂ ਕਾਲਜ ਵਿੱਚ 1965 ਵਿੱਚ, ਆਇਆ ਸੀ ਜਦੋਂ ਇਹ ਕੁੜਿੱਤਣ ਮੁੱਕਣ ਤੇ ਆ ਗਈ ਸੀ, ਜਦੋਂ  ਇਸ ਪ੍ਰਕਾਰ ਦੀਆਂ ਵਿਰੋਧਤਾਈਆਂ ਸਦਕਾ ਇਕ ਹੋਰ ਨੋਬਲ ਪੁਰਸਕਾਰ ਵਿਜੇਤਾ ਮਾਸਟਰ (Sir Nevill Mott) ਨੂੰ ਵੀ ਅਸਤੀਫ਼ਾ ਦੇਣਾ ਪੈ ਗਿਆ ਸੀ।

ਹੁਣ ਤੋਂ ਵੀਹ ਸਾਲ ਪਹਿਲਾਂ ਤੱਕ ਇਹ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ਕਿ ਪਰੋਟੋਨ ਅਤੇ ਨਿਊਟਰੋਨ ਮੁੱਢਲੇ ਕਣ ਹਨ, ਪਰੰਤੂ ਜਦੋਂ ਪਰੋਟੋਨਾਂ ਨੂੰ ਦੂਜੇ ਪਰੋਟੋਨਾਂ ਜਾਂ ਨਿਊਟਰੋਨਾਂ ਨਾਲ ਤਜ਼ਰਬੇ ਕਰਨ ਲਈ ਅੱਤ ਤੇਜ਼ ਰਫ਼ਤਾਰ ਨਾਲ ਟਕਰਾਇਆ ਜਾਂਦਾ ਸੀ, ਤਾਂ ਉਹ ਨਿੱਕੇ-ਨਿੱਕੇ ਕਣਾਂ (ਪ੍ਰਮਾਣੂਆਂ) ਦੇ ਬਣੇ ਹੋਏ ਹੁੰਦੇ ਸਨ। ਇਨ੍ਹਾਂ ਪ੍ਰਮਾਣੂਆਂ ਨੂੰ ਕੁਆਰਕ (Quarks) ਕਹਿੰਦੇ ਸੀ। 1969 ਵਿੱਚ ਇਨ੍ਹਾਂ ਉੱਤੇ ਤਜਰਬੇ ਕਰਨ ਸਦਕਾ ਕਾਲਟੈਕ डिसिवम भाव भने सैलभठ (Caltech Physics Murray Gell-Man) वविरा ਸੀ। ਇਨ੍ਹਾਂ ਦਾ ਨਾਮਕਰਨ ਜੇਮਜ਼ ਜੋਏਸ (James Joys) ਦੇ ਬੁਝਾਰਤੀ ਕਥਨ ਦੇ ਆਧਾਰ ‘ਤੇ ਹੋਇਆ ਸੀ। ਇਕ ਮਾਸਟਰ ਮਾਰਕ ਵਿੱਚ ਤਿੰਨ ਕੁਆਰਕ ਹੁੰਦੇ ਹਨ। ਇਸ ਸ਼ਬਦ ਦਾ ਉਚਾਰਨ ਕੁਆਰਟ ਵਾਂਗ ਹੈ, ਭਾਵੇਂ ਇਸ ਦੇ ਅੰਤ ਵਿੱਚ ਟੀ ਅੱਖਰ ਦੀ ਥਾਂ ਕੱਕਾ ਅੱਖਰ ਲੱਗਦਾ ਹੈ। ਇਸ ਦਾ ਸੁਰ ਲਾਰਕ ਨਾਲ ਮਿਲਦਾ ਹੈ।

ਕੁਆਰਕਾਂ ਦੀਆਂ ਕਈ ਵੰਨਗੀਆਂ ਹਨ। ਇਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਘੱਟੋ-ਘੱਟ ਛੇ ਹੈ— ਜਿਨ੍ਹਾਂ ਨੂੰ ਅਸੀਂ ਉੱਪਰ ਥੱਲੇ, ਅਨੋਖੇ, ਸੁੰਦਰ, ਪਾਤਾਲ ਅਤੇ ਟੀਸੀ ਕਹਿੰਦੇ ਹਾਂ। ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਹਰ ਇਕ ਦੇ ਤਿੰਨ ਰੰਗ ਮਿਲਦੇ ਹਨ-ਲਾਲ, ਹਰਾ ਅਤੇ ਨੀਲਾ। ਇਹ ਗੱਲਾਂ ਇਕ ਪ੍ਰਕਾਰ ਦੇ ਫਟੇ (ਛਾਪੇ) ਹੀ ਹਨ। ਕੁਆਰਕ ਦਿਸ ਰਹੀ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਦੀ ਲੰਬਾਈ ਨਾਲੋਂ ਬਹੁਤ ਛੋਟੇ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਵਿੱਚ ਕੋਈ ਵੀ ਰੰਗ ਨਹੀਂ ਹੁੰਦਾ। ਅਸਲ ਵਿੱਚ ਫਿਜ਼ਿਕਸ ਮਾਹਰ ਅਜਿਹੇ ਕਣਾਂ ਦੀ ਕਲਪਨਾ ਕਰਦੇ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਇਹ ਕਲਪਨਾ ਯੂਨਾਨੀ ਭਾਸ਼ਾ ਤੱਕ ਹੀ ਸੀਮਤ ਨਹੀਂ ਹੈ। ਇਕ ਪਰੋਟੋਨ ਜਾਂ ਨਿਊਟਰੋਨ ਵਿੱਚ ਤਿੰਨ ਕੁਆਰਕ ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਇੱਕੋ-ਇਕ ਰੰਗ ਮੌਜੂਦ ਹੁੰਦਾ ਹੈ। ਇਕ ਪਰੋਟੋਨ ਵਿੱਚ ਦੋ ਉੱਪਰਲੇ ਕੁਆਰਕ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਕ ਹੇਠਲਾ ਕੁਆਰਕ। ਇਕ ਨਿਟਰੋਨ ਵਿੱਚ ਦੋ ਹੇਠਲੇ ਕੁਆਰਕ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਕ ਉੱਪਰਲਾ। ਅਸੀਂ ਦੂਜੇ ਕੁਆਰਕਾਂ ਵਾਲੇ ਪ੍ਰਮਾਣੂ ਵੀ ਪੈਦਾ ਕਰ ਸਕਦੇ ਹਾਂ । ਅਨੋਖੇ, ਸੁੰਦਰ, ਪਾਤਾਲੀ ਅਤੇ ਟੀਸੀ ਵਾਲੇ।) ਪਰੰਤੂ ਇਨ੍ਹਾਂ ਸਾਰਿਆਂ ਦਾ ਸਮੂਹਕ ਆਕਾਰ ਬਹੁਤ ਵੱਡਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਛੇਤੀ ਹੀ ਪਰੋਟੋਨਾਂ ਅਤੇ ਇਹ ਨਿਊਟਰੋਨਾਂ ਵਿੱਚ ਢਲ ਜਾਂਦੇ ਹਨ।

ਹੁਣ ਸਾਨੂੰ ਗਿਆਨ ਹੋ ਗਿਆ ਹੈ ਕਿ ਐਟਮ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿਚਲੇ ਪਰੋਟੋਨ ਅਤੇ ਨਿਊਟਰੋਨ ਵੰਡੇ ਜਾਣ ਵਾਲੇ ਨਹੀਂ ਹੁੰਦੇ। ਇਸ ਲਈ ਪ੍ਰਸ਼ਨ ਪੈਦਾ ਹੁੰਦਾ ਹੈ : ਮੁੱਢਲੇ ਪ੍ਰਮਾਣੂ ਸੱਚਮੁੱਚ ਕੀ ਹਨ ? ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਸਭ ਕੁਝ ਪੈਦਾ ਹੋ ਜਾਂਦਾ ਹੈ ? ਕਿਉਂਕਿ ਰੌਸ਼ਨੀ ਦੀ ਲਹਿਰ ਦੀ ਲੰਬਾਈ ਐਟਮ ਦੇ ਆਕਾਰ ਨਾਲੋਂ ਬਹੁਤ ਵੱਡੀ ਹੁੰਦੀ ਹੈ, ਇਸ ਲਈ ਅਸੀਂ ਸਹਿਜ ਨਾਲ ਐਟਮ ਦੇ ਸਾਰੇ ਭਾਗਾਂ ਨੂੰ ਦੇਖਣ ਦੀ ਉਮੀਦ ਨਹੀਂ ਕਰ ਸਕਦੇ। ਸਾਨੂੰ ਅਤਿ ਛੋਟੀ ਲੰਬਾਈ ਵਾਲੀ ਲਹਿਰ ਵਰਤਣ ਦੀ ਲੋੜ ਪਵੇਗੀ। ਪਿਛਲੇ ਕਾਂਡ ਵਿੱਚ ਦੇਖ ਹੀ ਚੁੱਕੇ ਹਾਂ ਕਿ ਮਿਕਦਾਰੀ ਹਿਸਾਬ (Quantum Mechanics) ਦੁਆਰਾ ਪਤਾ ਲੱਗ ਜਾਂਦਾ ਹੈ ਕਿ ਸਾਰੇ ਪ੍ਰਮਾਣੂ ਅਸਲ ਵਿੱਚ ਲਹਿਰਾਂ ਹੀ ਹਨ ਅਤੇ ਕਿਸੇ ਪ੍ਰਮਾਣੂ ਵਿੱਚ ਜਿਤਨੀ ਵੱਧ ਸ਼ਕਤੀ ਹੋਵੇਗੀ, ਉਸ ਦੇ ਟਾਕਰੇ ਵਾਲੀ ਲਹਿਰ ਦੀ ਲੰਬਾਈ ਉਤਨੀ ਛੁਟੇਰੀ ਹੋਵੇਗੀ। ਇਸ ਲਈ ਪ੍ਰਸ਼ਨ ਦਾ ਉੱਤਰ ਇਸ ਗੱਲ ਉੱਤੇ ਨਿਰਭਰ ਹੈ ਕਿ ਸਾਡੇ ਕੋਲ ਪ੍ਰਮਾਣੂ ਦੀ ਸ਼ਕਤੀ ਕਿਤਨੀ ਜ਼ਿਆਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਨਿਰਣਾ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਅਸੀਂ ਕਿਤਨੀ ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਲੰਬਾਈ ਦੇਖ ਸਕਦੇ ਹਾਂ। ਪ੍ਰਮਾਣੂਆਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਇਲੈਕਟਰੋਨ ਵੋਲਟਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਨਾਪਿਆ ਜਾ ਸਕਦਾ ਹੈ। (ਥਾਮਸਨ ਦੇ ਇਲੈਕਟਰੋਨਾਂ ਦੇ ਤਜਰਬਿਆਂ ਦੇ ਦੌਰਾਨ ਅਸੀਂ ਦੇਖ ਲਿਆ ਸੀ ਕਿ ਉਸ ਨੇ ਇਲੈਕਟਰੋਨਾਂ ਦੀ ਰਫ਼ਤਾਰ ਤੇਜ਼ ਕਰਨ ਲਈ ਬਿਜਲਈ ਖੇਤਰ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਸੀ। ਬਿਜਲਈ ਖੇਤਰ ਦੇ ਇਕ ਵੋਲਟ ਵਿੱਚੋਂ ਜਿਤਨੀ ਸ਼ਕਤੀ ਕੋਈ ਇਲੈਕਟਰੋਨ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ, ਉਸ ਨੂੰ ਇਲੈਕਟਰੋਨ ਵੋਲਟ ਕਹਿੰਦੇ ਹਨ।) ਉਨੀਵੀਂ ਸ਼ਤਾਬਦੀ ਵਿੱਚ ਜਦੋਂ ਲੋਕਾਂ ਨੂੰ ਪ੍ਰਮਾਣੂ ਸ਼ਕਤੀ ਵਰਤਣ ਦਾ ਹੀ ਗਿਆਨ ਹੋਇਆ ਸੀ, ਉਹ ਇਲੈਕਟਰੋਨ ਵੋਲਟਾਂ ਦੀ ਘੱਟ ਤੋਂ ਘੱਟ ਸ਼ਕਤੀ ਹੀ ਸੀ ਜੋ ਕੀਮੀਆਈ ਢੰਗ ਨਾਲ ਪੈਦਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਸੀ, ਜਿਵੇਂ ਕਿ ਅੱਗ ਨਾਲ ਸੜਨ ਨਾਲ, ਇਹ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ਕਿ ਐਟਮ ਸਭ ਤੋਂ ਨਿੱਕੀ ਇਕਾਈ ਨੂੰ ਕਹਿੰਦੇ ਹਨ। ਰੂਥਰਫੋਰਡ ਦੇ ਤਜਰਬਿਆਂ ਦੇ ਦੌਰਾਨ ਅ-ਪ੍ਰਮਾਣੂ ਵਿੱਚ ਕਰੋੜਾਂ ਇਲੈਕਟਰੋਨ ਵੋਲਟਾਂ ਦੀ ਬਿਜਲੀ ਹੁੰਦੀ ਸੀ। ਹੁਣੇ-ਹੁਣੇ ਸਾਨੂੰ ਇਹ ਜਾਚ ਆ ਗਈ ਹੈ ਕਿ ਬਿਜਲਈ ਚੁੰਭਕ ਨੂੰ ਕਿਵੇਂ ਵਰਤੀਏ ਕਿ ਪ੍ਰਮਾਣੂ ਪਹਿਲਾਂ ਲੱਖਾਂ ਇਲੈਕਟਰੋਨ ਵੋਲਟ ਅਤੇ ਫੇਰ ਕਰੋੜਾਂ ਇਲੈਕਟਰੋਨ ਵੋਲਟ ਬਿਜਲੀ ਪੈਦਾ ਕਰ ਸਕਣ। ਇਸ ਲਈ ਅਸੀਂ ਜਾਣ ਗਏ ਹਾਂ ਕਿ ਵੀਹ ਸਾਲ ਪਹਿਲਾਂ ਜਿਹੜੇ ਪ੍ਰਮਾਣੂਆਂ ਨੂੰ ਅਸੀਂ ਮੁੱਢਲੇ ਪ੍ਰਮਾਣੂ ਹੀ ਕਿਆਸਦੇ ਸਾਂ, ਅਸਲ ਵਿੱਚ, ਉਹ ਬਹੁਤ ਸਾਰੇ ਨਿੱਕੇ-ਨਿੱਕੇ ਪ੍ਰਮਾਣੂਆਂ ਦੇ ਬਣੇ ਹੋਏ ਹਨ। ਜੇ ਅਸੀਂ ਵਧੇਰੇ ਤੋਂ ਵਧੇਰੇ ਬਿਜਲੀ ਪੈਦਾ ਕਰਦੇ ਜਾਵਾਂਗੇ, ਤਾਂ ਪਤਾ ਲੱਗੇਗਾ ਕਿ ਕੀ ਇਨ੍ਹਾਂ ਸਾਰੇ ਪ੍ਰਮਾਣੂਆਂ ਵਿੱਚ ਹੋਰ ਵੀ ਨਿੱਕੇ ਪ੍ਰਮਾਣੂ ਮੌਜੂਦ ਹਨ ? ਇਹ ਬਿਲਕੁਲ ਸੰਭਲਵ ਹੈ, ਪਰੰਤੂ ਇਸ ਵਿਸ਼ਵਾਸ ਦੇ ਕਿ ਸਾਨੂੰ ਅਜਿਹਾ ਗਿਆਨ ਹੋ ਚੁੱਕਾ ਹੈ, ਜਾਂ ਹੋਣ ਵਾਲਾ ਹੈ ਕਿ ਕੁਦਰਤ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਤੱਤਾਂ ਦੀ ਬਣੀ ਹੋਈ ਹੈ, ਕੁਝ ਸਿਧਾਂਤਕ ਕਾਰਨ ਵੀ ਹਨ।

ਪਿਛਲੇ ਕਾਂਡ ਵਿੱਚ ਜਿਸ ਲਹਿਰ-ਪ੍ਰਮਾਣੂ ਦੀ ਦੁਹਰੀ ਚਰਚਾ ਕੀਤੀ ਗਈ ਹੈ, ਉਸ ਦੀ ਵਰਤੋਂ ਨਾਲ ਕੁਦਰਤ ਦੇ ਹਰ ਇਕ ਤੱਤ, ਰੌਸ਼ਨੀ ਅਤੇ ਖਿੱਚ ਸਮੇਤ ਪ੍ਰਮਾਣੂਆਂ ਦੇ ਪੱਖੋਂ, ਵਿਆਖਿਆ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ। ਇਨ੍ਹਾਂ ਪ੍ਰਮਾਣੂਆਂ ਦੀ ਇਕ ਖੂਬੀ ਹੈ, ਜਿਸ ਨੂੰ ਘੁਮੇਰ ਕਹਿੰਦੇ ਹਨ। ਇਸ ਘੁਮੇਰ ਨੂੰ ਜਾਣਨ ਲਈ ਇਹ ਕਲਪਨਾ ਕਰਨੀ ਪਵੇਗੀ ਕਿ ਪ੍ਰਮਾਣੂ ਇਕ ਧੁਰੇ ਦੁਆਲੇ ਘੁੰਮਣ ਵਾਲੇ ਲਾਟੂ ਹਨ। ਪਰੰਤੂ ਅਜਿਹੀ ਕਲਪਨਾ ਭੁਲੇਖਾ ਪਾਊ ਸਿੱਧ ਹੋ ਸਕਦੀ ਹੈ ਕਿਉਂਕਿ ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਸਾਨੂੰ ਸਪੱਸ਼ਟ ਕਰਦਾ ਹੈ ਕਿ ਪ੍ਰਮਾਣੂਆਂ ਦਾ ਕੋਈ ਨਿਰਣਾਇਕ ਧੁਰਾ ਮੌਜੂਦ ਨਹੀਂ ਹੈ। ਕਿਸੇ ਪ੍ਰਮਾਣੂ ਦੀ ਘੁਮੇਰ ਤਾਂ ਸਾਨੂੰ ਕੇਵਲ ਇਹ ਦੱਸਦੀ ਹੈ ਕਿ ਭਿੰਨ-ਭਿੰਨ ਦਿਸ਼ਾਵਾਂ ਤੋਂ ਦੇਖਿਆਂ ਪ੍ਰਮਾਣੂ ਕਿਹੋ-ਜਿਹੇ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ। ਇਕ ਸਿਫ਼ਰ ਦੇ ਬਰਾਬਰ ਘੁਮੇਹ ਵਾਲਾ ਪ੍ਰਮਾਣੂ ਇਕ ਬਿੰਦੂ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ ਅਤੇ ਇਹ ਹਰ ਪਾਸਿਉਂ ਇਕੋ ਜਿਹਾ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ (ਤਸਵੀਰ 5- 2(i)। (ਚਿੱਤਰ) ਇਕ ਦੇ ਬਰਾਬਰ ਘੁਮੇਰ ਵਾਲਾ ਪ੍ਰਮਾਣੂ ਇਕ ਤੀਰ ਵਰਗਾ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ। ਇਹ ਹਰ ਇਕ ਦਿਸ਼ਾ ਤੋਂ ਵੱਖਰਾ-ਵੱਖਰਾ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ। ਤਸਵੀਰ 5-1 (ii)। (ਚਿੱਤਰ) ਕੇਵਲ ਜਦੋਂ ਇਹ 360 ਡਿਗਰੀ ਦਾ ਪੂਰਾ ਚੱਕਰ ਪੂਰਾ ਕਰਦਾ ਹੈ, ਉਦੋਂ ਇਹ ਪ੍ਰਮਾਣੂ ਇਕੋ ਜਿਹਾ ਨਜ਼ਰ ਆਵੇਗਾ। 2 ਚੱਕਰ ਕੱਟਣ ਵਾਲਾ ਪ੍ਰਮਾਣੂ ਦਾ ਸਿਰਾ ਤੀਰ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ। ਤਸਵੀਰ 5-1 (iii) (ਚਿੱਤਰ)। ਜੇ ਇਸ ਦਾ ਅੱਧਾ 180 ਡਿਗਰੀ ਗੇੜ ਦਿੱਤਾ ਜਾਵੇਂ ਤਾਂ ਇਹ ਇਕੋ ਜਿਹਾ ਨਜ਼ਰ ਆਵੇਗਾ। ਇਸੇ ਪ੍ਰਕਾਰ ਬਹੁਤ ਚੱਕਰ ਲਾਉਣ ਵਾਲਾ ਪ੍ਰਮਾਣੂ ਇਕੋ ਜਿਹਾ ਨਜ਼ਰ ਆਵੇਗਾ, ਜੇ ਇਸ ਦਾ ਪੂਰਾ

ਚੱਕਰ ਥੋੜ੍ਹਾ-ਥੋੜ੍ਹਾ ਕਰਕੇ ਕੀਤਾ ਜਾਵੇ। ਇਹ ਸਭ ਕੁਝ ਸਪੱਸ਼ਟ ਜਾਪਦਾ ਹੈ, ਪਰੰਤੂ ਮਾਰਕੇ ਵਾਲੀ ਗੱਲ ਤਾਂ ਇਹ ਹੈ ਕਿ ਅਜਿਹੇ ਪ੍ਰਮਾਣੂ ਵੀ ਹਨ ਜਿਹੜੇ ਇਕ ਪੂਰਾ ਗੇੜਾ ਦੇਣ ਉੱਤੇ ਇਕੋ ਜਿਹੇ ਨਜ਼ਰ ਨਹੀਂ ਆਉਂਦੇ। ਉਨ੍ਹਾਂ ਨੂੰ ਦੋ ਪੂਰੇ ਗੇੜੇ ਦੇਣੇ ਪੈਣਗੇ। ਅਜਿਹੇ ਪ੍ਰਮਾਣੂਆਂ ਨੂੰ 2 ਘੁਮੇਰ ਵਾਲੇ ਕਹਿੰਦੇ ਹਨ।

ਦੁਨੀਆਂ ਦੇ ਸਾਰੇ ਜਾਣੇ-ਪਛਾਣੇ ਪ੍ਰਮਾਣੂਆਂ ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ। 12 ਗੇੜੇ ਵਾਲੇ ਪ੍ਰਮਾਣੂ ਜਿਨ੍ਹਾਂ ਦੁਆਰਾ ਪਦਾਰਥ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ਅਤੇ 0, 1, 2 ਗੇੜਿਆਂ ਵਾਲੇ ਪ੍ਰਮਾਣੂ, ਜਿਨ੍ਹਾਂ ਦੁਆਰਾ ਅਸੀਂ ਦੇਖ ਲਵਾਂਗੇ, ਕਿ ਪਦਾਰਥ ਦੇ ਪ੍ਰਮਾਣੂਆਂ ਵਿਚਾਲੇ ਸ਼ਕਤੀਆਂ ਦੀ ਉਪਜ ਹੁੰਦੀ ਹੈ। ਪਦਾਰਥ ਪ੍ਰਮਾਣੂ ਪਾਲੀ (Pauli) ਦੇ ਨਿਖੇੜੂ ਸਿਧਾਂਤ ਦੇ ਆਗਿਆਕਾਰ ਹਨ। ਇਹ ਗੱਲ 1925 ਵਿੱਚ ਆਸਟ੍ਰੀਆ ਦੇ ਵੋਲਫਗੈਂਗ ਪਾਲੀ (Wolfgang Pauli) ਫਿਜ਼ਿਕਸ ਮਾਹਰ ਨੇ ਲੱਭੀ ਸੀ। ਜਿਸ ਪ੍ਰਾਪਤੀ ਕਰਕੇ ਉਸ ਨੂੰ 1945 ਵਿੱਚ ਨੋਬਲ ਪੁਰਸਕਾਰ ਮਿਲਿਆ ਸੀ। ਉਸ ਨੂੰ ਮੁੱਢਲੇ (ਅਸਲੀ) ਰੂਪ ਵਾਲਾ ਮਾਹਤ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ। ਕਹਿੰਦੇ ਸਨ ਕਿ ਕਿਸੇ ਵੀ ਸ਼ਹਿਰ ਵਿੱਚ ਉਸ ਦੀ ਮੌਜੂਦਗੀ ਲ ਤਜਰਬੇ ਗ਼ਲਤ ਹੋ ਜਾਂਦੇ ਸਨ। ਪਾਲੀ ਦਾ ਨਿਖੇੜੂ ਸਿਧਾਂਤ ਦੱਸਦਾ ਹੈ ਕਿ ਇੱਕੋ ਜਹੇ ਦੋ ਪ੍ਰਮਾਣੂ ਕਦੇ ਵੀ ਇੱਕੋ ਹਾਲਤ ਵਿੱਚ ਨਹੀਂ ਰਹਿ ਸਕਦੇ। ਅਰਥਾਤ ਨਾ ਤਾਂ ਦੋਹਾਂ ਦੀ ਇਕੋ ਜਿਹੀ ਹਾਲਤ ਹੋਵੇਗੀ ਅਤੇ ਨਾ ਹੀ ਅਨਿਸ਼ਚਿਤ ਸਿਧਾਂਤ ਦੀਆਂ ਉਲੀਕੀਆਂ ਹੱਦਾਂ ਅੰਦਰ, ਇਕੋ ਜਿਹੀ ਰਫ਼ਤਾਰ। ਨਿਖੇੜੂ ਸਿਧਾਂਤ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ, ਕਿਉਂਕਿ ਇਸ ਤੋਂ ਪਤਾ ਲੱਗ ਜਾਂਦਾ ਹੈ ਕਿ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂ, ਸਿਫ਼ਰ, ਇਕ ਅਤੇ 2 ਗੇੜਿਆਂ ਵਾਲੇ ਪ੍ਰਮਾਣੂਆਂ ਦੀਆਂ ਪੈਦਾ ਕੀਤੀਆਂ ਸ਼ਕਤੀਆਂ ਦੇ ਦਬਾਓ ਨਾਲ, ਗਾੜ੍ਹੇ ਹੋ ਕੇ ਨਸ਼ਟ ਕਿਉਂ ਨਹੀਂ ਹੋ ਜਾਂਦੇ।

ਜੇ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂਆਂ ਦੀ ਸਥਿਤੀ ਲਗਭਗ ਇਕੋ ਜਿਹੀ ਹੈ, ਤਾਂ ਉਨ੍ਹਾਂ ਦੀਆਂ ਰਫ਼ਤਾਰਾਂ ਭਿੰਨ-ਭਿੰਨ ਹੋਣਗੀਆਂ, ਅਰਥਾਤ ਉਹ ਬਹੁਤਾ ਚਿਰ ਇਕੋ ਸਥਿਤੀ ਵਿੱਚ ਨਹੀਂ ਰਹਿਣਗੇ। ਜੇ ਦੁਨੀਆਂ ਅਲਹਿਦਗੀ ਵਾਲੇ ਅਸੂਲ ਤੋਂ ਬਿਨਾਂ ਹੀ ਰਚੀ ਜਾਂਦੀ, ਤਾਂ ਕੁਆਰਕ ਵੱਖਰੇ, ਅਤੇ ਪ੍ਰਮਾਣਤ ਪਰੋਟੋਨ ਅਤੇ ਨਿਊਟਰੋਨ ਨਾ ਬਣ ਸਕਦੇ ਨਾ ਹੀ ਇਹ ਅਤੇ ਇਲੈਕਟਰੋਨ ਵੱਖਰੇ ਅਤੇ ਪ੍ਰਮਾਣਤ ਐਟਮ ਹੀ ਬਣ ਸਕਦੇ। ਉਹ ਸਾਰੇ ਢਹਿ-ਢੇਰੀ ਹੋ ਕੇ ਇਕੋ ਜਿਹੇ ਕੱਚ-ਘਰੜ ਜਿਹੇ ਗਾੜ੍ਹੇ “ਸੂਪ” (Soup) ਬਣ ਜਾਣੇ ਸਨ।

ਇਲੈਕਟਰੋਨਾਂ ਅਤੇ ਦੂਜੇ /2 ਗੇੜਿਆਂ ਵਾਲੇ ਪ੍ਰਮਾਣੂਆਂ ਦੀ 1928 ਤੱਕ ਪੂਰੀ ਸਮਝ ਨਹੀਂ ਸੀ ਪਈ ਜਦੋਂ ਪਾਲ ਡੀਰਾਕ (Paul Dirac) ਨੇ ਇਕ ਨਵਾਂ ਸਿਧਾਂਤ ਅਪਣਾਇਆ ਸੀ, ਅਤੇ ਜਿਸ ਨੂੰ ਕੁਝ ਚਿਰ ਪਿੱਛੋਂ ਕੈਂਬਰਿਜ ਵਿਖੇ ਲੁਕਾਸ਼ੀਅਨ ਪ੍ਰੋਫੈਸਰੀ ਲਈ ਚੁਣ ਲਿਆ ਗਿਆ ਸੀ। ਉਹੋ ਪ੍ਰੋਫੈਸਰੀ ਜੋ ਇਕ ਸਮੇਂ ਨਿਊਟਨ ਨੂੰ ਪ੍ਰਾਪਤ ਹੋਈ ਅਤੇ ਅੱਜ ਕੱਲ੍ਹ ਮੈਨੂੰ ਮਿਲੀ ਹੋਈ ਹੈ। ਡੀਰਾਕ ਦਾ ਸਿਧਾਂਤ ਇਸ ਕਿਸਮ ਦਾ ਪਹਿਲਾ ਸਿਧਾਂਤ ਸੀ, ਅਤੇ ਇਹ ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਅਤੇ ਅਨੁਪਾਤ ਦੇ ਵਿਸ਼ੇਸ਼ ਸਿਧਾਂਤ ਦੋਹਾਂ ਦੇ ਅਨੁਕੂਲ ਸੀ। ਇਸ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਸੀ ਕਿ ਹਿਸਾਬ ਅਨੁਸਾਰ ਇਲੈਕਟਰੋਨ ਦਾ 2 ਗੇੜਾ ਕਿਉਂ ਲਗਾਂਦਾ ਸੀ। ਅਰਥਾਤ ਇਸ ਨੂੰ ਇਕ ਪੂਰਾ ਗੇੜਾ ਦੇਣ ਉੱਤੇ ਇਹ ਇਕੋ ਜਿਹਾ ਕਿਉਂ ਨਜ਼ਰ ਨਹੀਂ ਆਉਂਦਾ। ਪਰੰਤੂ ਦੋ ਗੇੜੇ ਦੇਣ ਉੱਤੇ ਇਕੋ ਜਿਹਾ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ। ਇਸ ਸਿਧਾਂਤ ਤੋਂ ਇਹ ਵੀ ਪਤਾ ਲੱਗ ਜਾਂਦਾ ਹੈ ਕਿ ਇਲੈਕਟਰੋਨ ਨੂੰ ਭਾਈਵਾਲ ਦੀ ਵੀ ਲੋੜ ਹੈ, ਜੋ ਇਲੈਕਟਰੋਨ ਵਿਰੋਧੀ ਜਾਂ ਪੋਜ਼ੀਟਰੋਨ (Positron) ਕਿਹਾ ਜਾਂਦਾ ਹੈ। 1932 ਵਿੱਚ ਪੋਜ਼ੀਟਰੋਨ ਦੀ ਭਾਲ ਸਦਕਾ ਡੀਰਾਕ ਦੇ ਸਿਧਾਂਤ ਦੀ ਪ੍ਰਸ਼ਟੀ ਹੋ ਗਈ ਸੀ ਤੇ 1933 ਵਿੱਚ ਉਸ ਨੂੰ ਇਸ ਲਈ ਨੋਬਲ ਪੁਰਸਕਾਰ ਪ੍ਰਾਪਤ ਹੋ ਗਿਆ ਸੀ । ਹੁਣ ਸਾਨੂੰ ਪਤਾ ਹੈ ਕਿ ਹਰ ਇਕ ਪ੍ਰਮਾਣੂ ਦਾ ਵਿਰੋਧੀ ਪ੍ਰਮਾਣੂ ਵੀ ਹੁੰਦਾ ਹੈ, ਜੋ ਇਸ ਦਾ ਵਿਨਾਸ਼ ਕਰ ਦਿੰਦਾ ਹੈ। (ਸ਼ਕਤੀਸ਼ਾਲੀ ਪ੍ਰਮਾਣੂਆਂ ਦੀ ਸੂਰਤ ਵਿੱਚ, ਵਿਰੋਧੀ ਪ੍ਰਮਾਣੂ ਇਨ੍ਹਾਂ ਪ੍ਰਮਾਣੂਆਂ ਵਰਗੇ ਹੀ ਹੁੰਦੇ ਹਨ) ਦੁਨੀਆਂ ਵਿਰੋਧੀ ਅਤੇ ਲੋਕ-ਵਿਰੋਧੀ ਤੱਤ ਇਨ੍ਹਾਂ ਪ੍ਰਮਾਣੂ-ਵਿਰੋਧੀ ਤੱਤਾਂ ਦਾ ਨਤੀਜਾ ਹਨ। ਜੇ ਤੁਸੀਂ ਕਿਸੇ ਸਵੈ-ਵਿਰੋਧੀ ਨੂੰ ਮਿਲੋ, ਤਾਂ ਉਸ ਨਾਲ ਹੱਥ ਨਾ ਮਿਲਾਓ। ਤੁਸੀਂ ਦੋਵੇਂ ਰੌਸ਼ਨੀ ਦੇ ਇਕੋ ਲਿਸ਼ਕਾਰੇ ਵਿੱਚ ਨਸ਼ਟ ਹੋ ਜਾਉਗੇ। ਇਹ ਪ੍ਰਸ਼ਨ ਕਿ ਵਿਰੋਧੀ ਪ੍ਰਮਾਣੂਆਂ ਨਾਲੋਂ ਇਤਨੇ ਵਾਧੂ ਪ੍ਰਮਾਣੂ ਕਿਉਂ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ, ਅਤਿ ਜ਼ਰੂਰੀ ਹੈ ਅਤੇ ਇਸ ਕਾਂਡ ਵਿੱਚ ਅੱਗੇ ਚੱਲ ਕੇ ਇਸ ਦੀ ਚਰਚਾ ਕੀਤੀ ਜਾਵੇਗੀ। ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਅਨੁਸਾਰ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂਆਂ ਦੀ ਆਪਸੀ ਖਹਿਬਾਜ਼ੀ ਜਾਂ ਇਨ੍ਹਾਂ ਵਿਚਲੀ ਸ਼ਕਤੀ 0, 1 ਜਾਂ 2 ਸਾਲਮ ਗੇੜਿਆਂ ਵਾਲੇ ਪ੍ਰਮਾਣੂਆਂ ਵਿੱਚ ਮੌਜੂਦ ਹੁੰਦੀ ਹੈ। ਹੁੰਦਾ ਐਉਂ ਹੈ ਕਿ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂ, ਜਿਵੇਂ ਕਿ ਇਕ ਇਲੈਕਟਰੋਨ ਜਾਂ ਇਕ ਧੁਆਰਕ ਵਿੱਚੋਂ ਸ਼ਕਤੀ ਭਰਪੂਰ ਪ੍ਰਮਾਣੂ ਪੈਦਾ ਹੁੰਦਾ ਹੈ। ਇਸ ਦੀ ਗੋਲਾਈ ਨਾਲ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂ ਦੀ ਰਫ਼ਤਾਰ ਬਦਲ ਜਾਂਦੀ ਹੈ। ਸ਼ਕਤੀ-ਭਰਪੂਰ ਪ੍ਰਮਾਣੂ ਫੇਰ ਕਿਸੇ ਦੂਜੇ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂ ਨਾਲ ਟਕਰਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਉਸ ਨਾਲ ਇਕਮਿਕ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਟਕਰਾਓ ਨਾਲ ਦੂਜੇ ਪ੍ਰਮਾਣੂ ਦੀ ਰਫ਼ਤਾਰ ਬਦਲ ਜਾਂਦੀ ਹੈ। ਐਨ ਇਸ ਤਰ੍ਹਾਂ ਜਿਵੇਂ ਦੋਹਾਂ ਪ੍ਰਮਾਣੂਆਂ ਵਿਚਕਾਰ ਕੋਈ ਸ਼ਕਤੀ ਮੌਜੂਦ ਹੋਵੇ।

ਸ਼ਕਤੀ ਭਰਪੂਰ ਪ੍ਰਮਾਣੂਆਂ ਦੀ ਇਹ ਖ਼ੂਬੀ ਹੈ ਕਿ ਉਹ ਅਲਹਿਦਗੀ ਦੇ ਅਸੂਲ ਦੀ ਪਾਲਣਾ ਨਹੀਂ ਕਰਦੇ। ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਅਦਲਾ-ਬਦਲੀ ਕਰਨ ਵਾਲੇ ਅੰਕਾਂ ਦੀ ਗਿਣਤੀ ਨਹੀਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਅਤੇ ਨਤੀਜੇ ਵਜੋਂ ਅਥਾਹ ਸ਼ਕਤੀ ਪੈਦਾ ਹੋ ਸਕਦੀ ਹੈ। ਪਰੰਤੂ, ਜੇ ਸ਼ਕਤੀ ਭਰਪੂਰ ਪ੍ਰਮਾਣੂਆਂ ਦਾ ਆਕਾਰ ਬਹੁਤ ਵੱਡਾ ਹੋਵੇ ਤਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਪੈਦਾ ਕਰਨ ਅਤੇ ਦੂਰ ਤੱਕ ਉਨ੍ਹਾਂ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਅਤਿ ਕਠਿਨ ਹੈ। ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਵਿਚਲੀ ਸ਼ਕਤੀ ਦੀ ਮਾਰ ਬਹੁਤੀ ਨਹੀਂ ਹੋਵੇਗੀ। ਦੂਜੇ ਬੰਨੇ ਜੇ ਅਜਿਹੇ ਪ੍ਰਮਾਣੂਆਂ ਦਾ ਆਪਣਾ ਕੋਈ ਆਕਾਰ ਹੀ ਨਾ ਹੋਵੇ ਤਾਂ ਸ਼ਕਤੀ ਦੀ ਮਾਰ ਵਧੇਰੇ ਹੋਵੇਗੀ। ਸ਼ਕਤੀ ਭਰਪੂਰ ਪ੍ਰਮਾਣੂ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂਆਂ ਵਿੱਚ ਬਦਲਣ ਉਪਰੰਤ ਅਸਲ ਪ੍ਰਮਾਣੂ ਬਣ ਜਾਂਦੇ ਹਨ, ਕਿਉਂਕਿ ਅਸਲੀ ਪ੍ਰਮਾਣੂਆਂ ਵਾਂਗ ਉਨ੍ਹਾਂ ਨੂੰ ਜੰਤਰ ਨਾਲ ਲੱਭਿਆ ਨਹੀਂ ਜਾ ਸਕਦਾ। ਫੇਰ ਵੀ ਸਾਨੂੰ ਪਤਾ ਹੈ ਕਿ ਉਹ ਮੌਜੂਦ ਹਨ ਕਿਉਂਕਿ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਣਿਆ ਜਾ ਸਕਦਾ ਹੈ। ਭਾਵ ਉਹ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂਆਂ ਵਿਚਕਾਰ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰ ਦਿੰਦੇ ਹਨ। ਕੁਝ ਹਾਲਤਾਂ ਵਿੱਚ, 0, 1 ਜਾਂ 2 ਗੇੜਿਆਂ ਵਾਲੇ ਪ੍ਰਮਾਣੂ, ਅਸਲੀ ਪ੍ਰਮਾਣੂਆਂ ਦੇ ਰੂਪ ਵਿੱਚ ਮੌਜੂਦ ਹੋ ਸਕਦੇ ਹਨ। ਜਦੋਂ ਉਨ੍ਹਾਂ ਨੂੰ ਸਿੱਧੇ ਢੰਗ ਨਾਲ ਹੀ ਲੱਭਿਆ ਜਾ ਸਕੇ। ਉਹ ਫੇਰ ਸਾਨੂੰ ਇਕ ਤਜਰਬੇਕਾਰ ਫਿਜ਼ਿਕਸ ਮਾਹਰ ਅਨੁਸਾਰ ਲਹਿਰਾਂ ਵਰਗੇ ਜਾਪਣਗੇ : ਰੌਸ਼ਨੀ ਜਾਂ ਚੁੰਭਕੀ ਲਹਿਰਾਂ ਵਰਗੇ। ਉਹ ਕਦੇ-ਕਦੇ ਉਸ ਵੇਲੇ ਪੈਦਾ ਹੋ ਸਕਦੇ ਹਨ, ਜਦੋਂ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂ ਅਸਲੀ ਸ਼ਕਤੀ ਭਰਪੂਰ ਪ੍ਰਮਾਣੂਆਂ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਕਰਨ ਸਮੇਂ ਆਪੋ ਵਿੱਚ ਕਰਾਉਂਦੇ ਹਨ। ਉਦਾਹਰਣ ਵਜੋਂ ਦੋ ਇਲੈਕਟਰੋਨਾਂ ਵਿੱਚ ਬਿਜਲੀ ਦੀ ਰੁਕਾਵਟ ਪਾਉਣ ਵਾਲੀ ਸ਼ਕਤੀ, ਜੋ ਪੱਕੇ ਫੋਟੋਨ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਸਮੇਂ ਪੈਦਾ ਹੋਇਆ ਕਰਦੀ ਹੈ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਸਿੱਧੇ ਢੰਗ ਨਾਲ ਦੇਖਿਆ ਨਹੀਂ ਜਾ ਸਕਦਾ। ਪਰੰਤੂ ਜੇ ਇਕ ਇਲੈਕਟਰੋਨ ਦੂਜੇ ਕੋਲੋਂ ਅੱਗੇ ਲੰਘ ਜਾਵੇ, ਅਸਲੀ ਫੋਟੋਨ ਪੈਦਾ ਹੋ ਸਕਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਰੌਸ਼ਨੀ ਦੀਆਂ ਲਹਿਰਾਂ ਵਾਂਗ ਲੱਭਿਆ ਜਾ ਸਕਦਾ ।

ਸ਼ਕਤੀ-ਭਰਪੂਰ ਪ੍ਰਮਾਣੂਆਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਕਤੀ ਦੀ ਮਾਤਰਾ ਅਨੁਸਾਰ ਚਾਰ ਵਰਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਪ੍ਰਮਾਣੂਆਂ ਨੂੰ ਮੁਖ ਰੱਖ ਕੇ, ਜਿਨ੍ਹਾਂ ਨਾਲ ਉਹ ਟਕਰਾਉਂਦੇ ਹੋਣ। ਇਸ ਗੱਲ ਉੱਤੇ ਜ਼ੋਰ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਇਹ ਚਾਰ ਵਰਗਾਂ ਵਿਚਲੀ ਵੰਡ ਮਨੁੱਖ ਦੀ ਦੇਣ ਹੀ ਹੈ। ਇਸ ਦੁਆਰਾ ਅੰਸ਼ਕ ਸਿਧਾਂਤ ਘੜਨੇ ਸੌਖੇ ਹਨ, ਪਰੰਤੂ ਇਨ੍ਹਾਂ ਦੀ ਪਕਿਆਈ ਕੋਈ ਨਹੀਂ ਹੈ। ਆਖ਼ਰ, ਬਹੁਤ ਸਾਰੇ ਫਿਜ਼ਿਕਸ ਮਾਹਰ ਇਕ ਮਿਲਿਆ ਜੁਲਿਆ ਸਿਧਾਂਤ ਲੱਭਣ ਦੀ ਉਮੀਦ ਲਾਈ ਬੈਠੇ ਹਨ, ਜਿਸ ਦੁਆਰਾ ਇਨ੍ਹਾਂ ਚਾਰਾਂ ਸ਼ਕਤੀਆਂ ਦੀ ਵਿਆਖਿਆ ਇਕੋ ਸ਼ਕਤੀ ਦੇ ਰੂਪ ਵਿੱਚ ਕੀਤੀ ਜਾ ਸਕੇਗੀ। ਸੱਚੀ ਗੱਲ ਤਾਂ ਇਹ ਹੈ ਕਿ ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਬਹੁਤੇ ਇਸ ਨੂੰ ਇਸ ਸਮੇਂ ਫਿਜ਼ਿਕਸ ਦੀ ਸਭ ਤੋਂ ਮੁੱਢਲੀ ਲੋੜ ਸਮਝਦੇ ਹਨ। ਥੋੜ੍ਹਾ ਸਮਾਂ ਪਹਿਲਾਂ ਸ਼ਕਤੀ ਦੇ ਚਾਰਾਂ ਪੱਖਾਂ ਵਿੱਚੋਂ ਤਿੰਨ ਸ਼ਕਤੀਆਂ ਦੇ ਏਕੀਕਰਨ ਦੀਆਂ ਸਫ਼ਲ ਕੋਸ਼ਿਸ਼ਾਂ ਹੋਈਆਂ ਵੀ ਹਨ ਅਤੇ ਮੈਂ ਇਨ੍ਹਾਂ ਦੀ ਚਰਚਾ ਇਸ ਕਾਂਡ ਵਿੱਚ ਕਰ ਰਿਹਾ ਹਾਂ। ਚੌਥੀ ਸ਼ਕਤੀ, ਚੁੰਭਕੀ ਸ਼ਕਤੀ ਨੂੰ ਜੋੜਨ ਦਾ ਪ੍ਰਸ਼ਨ ਕਦੇ ਫੇਰ, ਪਛੜ ਕੇ ਕੀਤਾ ਜਾਵੇਗਾ।

ਪਹਿਲੀ ਸ਼ਕਤੀ ਚੁੰਭਕੀ ਸ਼ਕਤੀ ਹੈ। ਜੋ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਹੈ, ਅਰਥਾਤ ਹਰ ਇਕ ਪ੍ਰਮਾਣੂ ਇਸ ਸ਼ਕਤੀ ਤੋਂ ਪ੍ਰਭਾਵਤ ਹੁੰਦਾ ਹੈ। ਇਸ ਦੇ ਆਕਾਰ ਅਤੇ ਸ਼ਕਤੀ ਦੇ ਆਧਾਰ ਤੇ ਚੁੰਭਕ ਸ਼ਕਤੀ ਚਾਰਾਂ ਸ਼ਕਤੀਆਂ ਵਿੱਚੋਂ ਸਭ ਤੋਂ ਕਮਜ਼ੋਰ ਹੈ, ਇਤਨੀ ਕਮਜ਼ੋਰ ਕਿ ਇਸ ਦੇ ਦੋ ਗੁਣਾਂ ਤੋਂ ਬਿਨਾਂ, ਅਸੀਂ ਇਸ ਨੂੰ ਅਨੁਭਵ ਹੀ ਨਹੀਂ ਕਰ ਸਕਦੇ, ਇਹ ਦੂਰ ਤੱਕ ਕੰਮ ਕਰ ਸਕਦੀ ਹੈ ਅਤੇ ਇਹ ਸਦਾ ਹੀ ਦਿਲ ਖਿੱਚਵੀਆਂ ਹੋਇਆ ਕਰਦੀਆਂ ਹਨ। ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਧਰਤੀ ਅਤੇ ਸੂਰਜ ਵਰਗੀਆਂ ਦੋ ਵੱਡੀਆਂ ਵਸਤਾਂ ਦੇ ਆਪਣੇ-ਆਪਣੇ ਪ੍ਰਮਾਣੂਆਂ ਦੇ ਵਿਚਕਾਰ, ਇਹ ਕਮਜ਼ੋਰ ਸ਼ਕਤੀਆਂ ਇਕੱਠੀਆਂ ਹੋ ਕੇ ਇਕ ਬਹੁਤ ਵੱਡੀ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰ ਸਕਦੀਆਂ ਹਨ। ਦੂਜੀਆਂ ਤਿੰਨ ਸ਼ਕਤੀਆਂ ਜਾਂ ਤਾਂ ਛੁਟੇਰੀ ਮਾਰ ਕਰਨ ਵਾਲੀਆਂ ਹਨ, ਜਾਂ ਕਦੇ ਦਿਲ-ਖਿਚਵੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਕਦੇ ਰੁਕਾਵਟ ਪਾਉਣ ਵਾਲੀਆਂ, ਇਸ ਲਈ ਇਕ ਦੂਜੀ ਨੂੰ ਰੱਦ ਕਰ ਦਿੰਦੀਆਂ ਹਨ। ਮਿਕਦਾਰੀ ਹਿਸਾਬ ਦੇ ਪੱਖੋਂ ਦੇਖਿਆਂ, ਚੁੰਭਕੀ ਖੇਤਰ, ਅਰਥਾਤ ਦੋ ਪਦਾਰਥਕ ਪ੍ਰਮਾਣੂਆਂ ਵਿਚਲੀ ਸ਼ਕਤੀ ਐਉਂ ਪ੍ਰਤੀਤ ਹੁੰਦੀ ਹੈ ਕਿ ਇਸ ਨੂੰ 2 ਗੇੜਿਆਂ ਵਾਲਾ ਪ੍ਰਮਾਣੂ ਲਿਜਾ ਰਿਹਾ ਹੈ, ਜਿਸ ਨੂੰ ਗਰੈਵੀਟੋਨ (Graviton) ਕਹਿੰਦੇ ਹਨ। ਇਸ ਦਾ ਆਪਣਾ ਕੋਈ ਆਕਾਰ ਨਹੀਂ ਹੈ, ਇਸ ਲਈ ਇਸ ਵਿਚਲੀ ਸ਼ਕਤੀ ਦੂਰ ਤੱਕ ਮਾਰ ਕਰਨ ਵਾਲੀ ਹੁੰਦੀ ਹੈ। ਸੂਰਜ ਅਤੇ ਧਰਤੀ ਵਿਚਕਾਰਲੀ ਚੁੰਭਕੀ ਸ਼ਕਤੀ ਨੂੰ ਉਨ੍ਹਾਂ ਪ੍ਰਮਾਣੂਆਂ ਵਿਚਲੇ ਗਰੈਵੀਟੋਨ (Graviton) ਕਹਿੰਦੇ ਹਨ। ਇਸ ਦਾ ਆਪਣਾ ਕੋਈ ਆਕਾਰ ਨਹੀਂ ਹੈ, ਇਸ ਲਈ ਇਸ ਵਿਚਲੀ ਸ਼ਕਤੀ ਦੂਰ ਤੱਕ ਮਾਰ ਕਰਨ ਵਾਲੀ ਹੁੰਦੀ ਹੈ। ਸੂਰਜ ਅਤੇ ਧਰਤੀ ਵਿਚਕਾਰਲੀ ਚੁੰਭਕੀ ਸ਼ਕਤੀ ਨੂੰ ਪ੍ਰਮਾਣੂਆਂ ਵਿਚਲੇ ਗਰੈਵੀਟੋਨਾਂ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਦਾ ਨਤੀਜਾ ਦੱਸਿਆ ਜਾਂਦਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਨਾਲ ਇਹ ਦੋਵੇਂ ਵਸਤਾਂ ਬਣੀਆਂ ਹੋਈਆਂ ਹਨ। ਭਾਵੇਂ ਇਹ ਬਦਲਵੇਂ ਪ੍ਰਮਾਣੂ ਚੰਗੇ ਹਨ, ਉਹ ਮਿਣੇ ਜਾਣ ਵਾਲੇ ਪ੍ਰਭਾਵ ਪੈਦਾ ਕਰਦੇ ਹਨ—ਇਨ੍ਹਾਂ ਸਦਕਾ ਹੀ ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮ ਰਹੀ ਹੈ। ਅਸਲ ਗਰੈਵੀਟੋਨਾਂ ਨੂੰ ਪ੍ਰਸਿੱਧ ਫਿਜ਼ਿਕਸ ਮਾਹਰ ਚੁੰਬਕੀ ਲਹਿਰਾਂ ਕਹਿੰਦੇ ਹਨ, ਜਿਹੜੀਆਂ ਬਹੂਤ ਕਮਜ਼ੋਰ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਅਨੁਭਵ ਕਰਨਾ ਇਤਨਾ ਕਠਿਨ ਹੈ ਕਿ ਹਾਲੇ ਤੱਕ ਉਨ੍ਹਾਂ ਨੂੰ ਕੋਈ ਵੀ ਦੇਖ ਨਹੀਂ ਸਕਿਆ।

ਅਸਲੀ ਵੰਨਗੀ ਬਿਜਲਈ ਚੰਬਕ (Electromagnetic) ਸ਼ਕਤੀ ਹੈ, ਜਿਹੜੀ ਇਲੈਕਟਰੋਨਾਂ ਅਤੇ ਕੁਆਰਕਾਂ ਵਰਗੇ ਬਿਜਲੀ-ਭਰਪੂਰ ਪ੍ਰਮਾਣੂਆਂ ਨਾਲ ਟਕਰਾਉਂਦੀ ਹੈ, ਗਰੈਵੀਟੋਨਾਂ ਵਰਗੇ ਬਿਜਲੀ-ਰਹਿਤ ਪ੍ਰਮਾਣੂਆਂ ਨਾਲ ਨਹੀਂ ਟਕਰਾਉਂਦੀ।

 

Credit – ਸਟੀਫਨ ਡਬਲਿਊ ਹਾਕਿੰਗ, ਗੁਰਦਿੱਤ ਸਿੰਘ ਕੰਗ